八年级物理暑期专题07 不规则容器的液体压强（原卷版+解析版）-2022-2023学年八年级物理下册学优生期末复习难点题型专项突破（人教版）

这是一份八年级物理暑期专题07 不规则容器的液体压强（原卷版+解析版）-2022-2023学年八年级物理下册学优生期末复习难点题型专项突破（人教版），文件包含八年级物理暑期专题07不规则容器的液体压强解析版-2022-2023学年八年级物理下册学优生期末复习难点题型专项突破人教版docx、八年级物理暑期专题07不规则容器的液体压强原卷版-2022-2023学年八年级物理下册学优生期末复习难点题型专项突破人教版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
专题07 不规则容器的液体压强
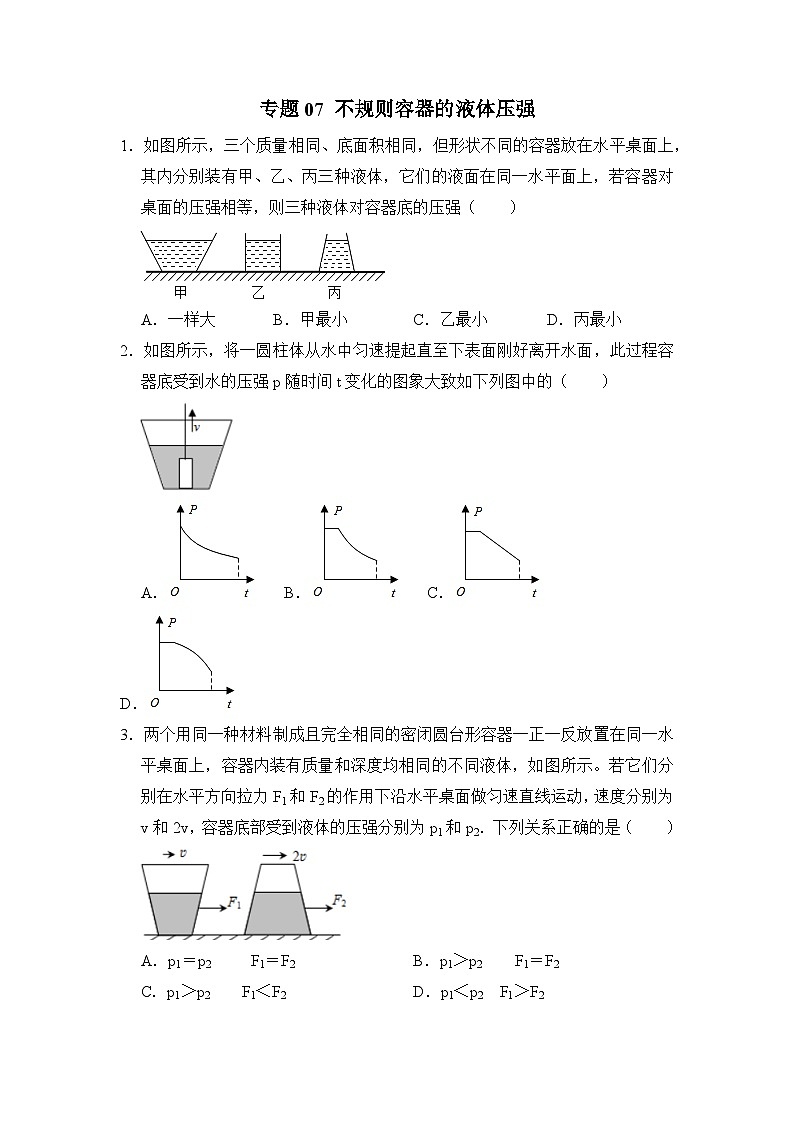
1．如图所示，三个质量相同、底面积相同，但形状不同的容器放在水平桌面上，其内分别装有甲、乙、丙三种液体，它们的液面在同一水平面上，若容器对桌面的压强相等，则三种液体对容器底的压强（　　）

A．一样大 B．甲最小 C．乙最小 D．丙最小
解：三个容器质量相同，由公式G＝mg可知，三个容器的重力G容相同，
三个容器对桌面的压强相等，且三个容器的底面积相同，由公式F＝pS可知三个容器对水平桌面的压力相同，而容器对水平桌面的压力为F＝G容+G液，则三个容器中的液体重力G液相同，
由图示可知，三种液体的体积大小关系为：V甲＞V乙＞V丙，
由公式G＝mg＝ρVg可得：ρ=G液V液g，由此可知，三种液体的密度大小关系为ρ甲＜ρ乙＜ρ丙，
根据题意可知三个容器中液体深度相同，由公式p＝ρ液gh可知，液体对容器底的压强大小关系为：p甲＜p乙＜p丙，
即甲液体对容器底的压强最小，故B正确，A、C、D错误。
答案：B。
2．如图所示，将一圆柱体从水中匀速提起直至下表面刚好离开水面，此过程容器底受到水的压强p随时间t变化的图象大致如下列图中的（　　）

A． B． C． D．
解：①将一圆柱体从水中匀速提起至其上表面刚好露出水面之前，水的密度一定，容器内水的深度不变，根据p＝ρgh可知，容器底受到水的压强不变；
②从圆柱体上表面刚露出水面到圆柱体直至下表面刚好离开水面的过程中，圆柱体排开水的体积减小，容器内水的深度逐渐减小；由于圆柱体被匀速提起，容器的形状上粗下细，根据ΔV排＝SΔh可知，水的深度减小的越来越快，根据p＝ρgh可知，容器底受到水的压强逐渐变小，并且也是减小得越来越快。符合这个规律的只有D图象，故ABC错误，D正确。
答案：D。
3．两个用同一种材料制成且完全相同的密闭圆台形容器一正一反放置在同一水平桌面上，容器内装有质量和深度均相同的不同液体，如图所示。若它们分别在水平方向拉力F1和F2的作用下沿水平桌面做匀速直线运动，速度分别为v和2v，容器底部受到液体的压强分别为p1和p2．下列关系正确的是（　　）

A．p1＝p2 F1＝F2 B．p1＞p2 F1＝F2
C．p1＞p2 F1＜F2 D．p1＜p2　F1＞F2
解：容器内装有质量和深度均相同的不同液体，由图可知，V1＜V2，
根据ρ=mV可知，两种液体的密度ρ1＞ρ2；
由p＝ρ液gh可知，容器底部受到液体的压强p1＞p2；
容器质量相同，内装液体的质量相同，则容器对桌面的压力相等，
又因为容器材料相同，放置在同一水平桌面上，即接触面的粗糙程度相同，
所以容器与桌面间的摩擦力相等，
在水平方向拉力F1和F2的作用下沿桌面做匀速直线运动，
所以拉力与摩擦力是一对平衡力，大小相等，即：F1＝F2。
由上分析知，ACD错误，B正确。
答案：B。
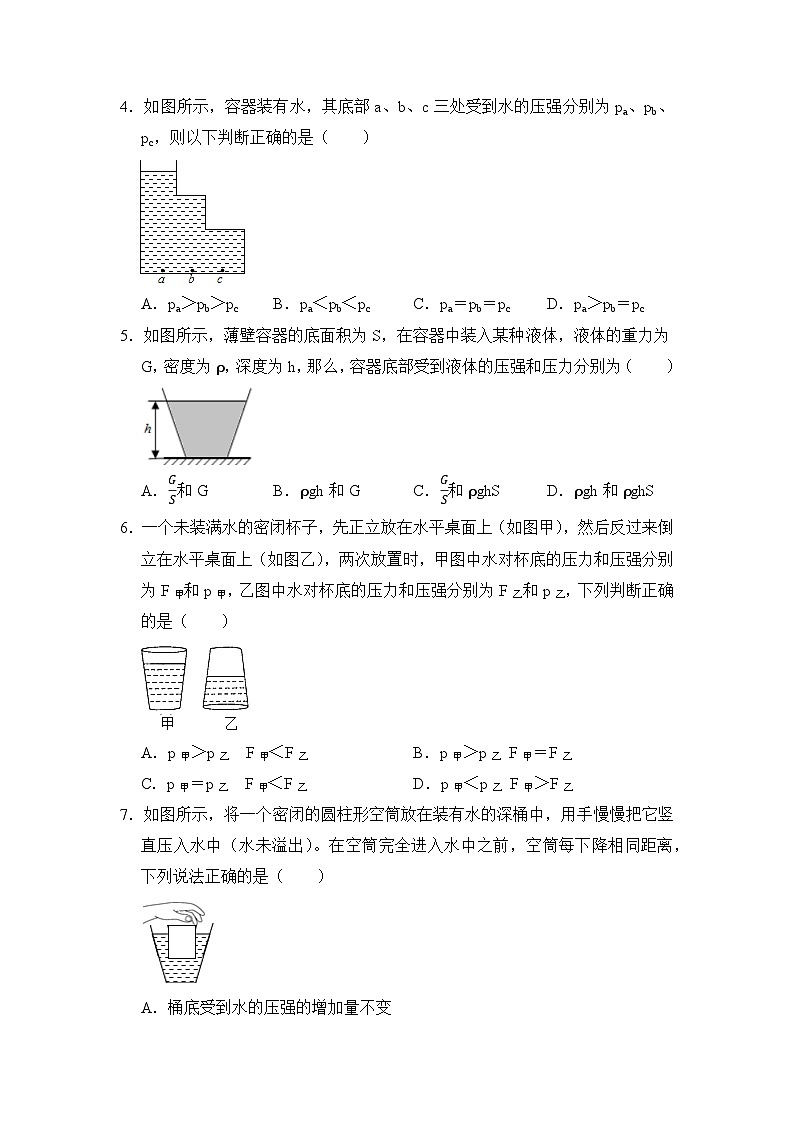
4．如图所示，容器装有水，其底部a、b、c三处受到水的压强分别为pa、pb、pc，则以下判断正确的是（　　）

A．pa＞pb＞pc B．pa＜pb＜pc C．pa＝pb＝pc D．pa＞pb＝pc
解：由图知：容器底部a、b、c三处水的深度相同，水的密度确定，由公式p＝ρgh知：此三点受到水的压强相同。
答案：C。
5．如图所示，薄壁容器的底面积为S，在容器中装入某种液体，液体的重力为G，密度为ρ，深度为h，那么，容器底部受到液体的压强和压力分别为（　　）

A．GS和G B．ρgh和G C．GS和ρghS D．ρgh和ρghS
解：某种液体的深度为h，则p＝ρgh，
由p=FS可得，容器底部受到液体的压力：F＝pS＝ρghS。
答案：D。
6．一个未装满水的密闭杯子，先正立放在水平桌面上（如图甲），然后反过来倒立在水平桌面上（如图乙），两次放置时，甲图中水对杯底的压力和压强分别为F甲和p甲，乙图中水对杯底的压力和压强分别为F乙和p乙，下列判断正确的是（　　）

A．p甲＞p乙 F甲＜F乙 B．p甲＞p乙 F甲＝F乙
C．p甲＝p乙 F甲＜F乙 D．p甲＜p乙 F甲＞F乙
解：
（1）由于杯子是上粗下细，所以倒立时，杯中液面的高度要小于正立时的液面高度；
根据p＝ρgh可知：当水密度相同时，水面越高，水对杯底的压强越大，所以p甲＞p乙；
（2）当容器形状是上粗下细（如图甲）时，对容器底的压力小于水重力，即F＜G；当容器形状是上细下粗（如图乙）时，对容器底的压力大于水重力，即F＞G；可见F甲＜G，F乙＞G，故F乙＞F甲；
答案：A。
7．如图所示，将一个密闭的圆柱形空筒放在装有水的深桶中，用手慢慢把它竖直压入水中（水未溢出）。在空筒完全进入水中之前，空筒每下降相同距离，下列说法正确的是（　　）

A．桶底受到水的压强的增加量不变
B．桶底受到水的压强的增加量变大
C．空筒底部受到水的压强的增加量不变
D．空筒底部受到水的压强的增加量变小
解：在空筒完全进入水中之前，空筒下降时，水面会随之升高，由于桶的横截面积下小上大，空筒每下降相同距离，水面上升的高度变化量和筒浸入水中深度的增加量变小，根据Δp＝ρgΔh可知，桶底受到水的压强增加量和空筒底部受到水的压强增加量均会变小，故D正确。
答案：D。
8．如图所示，三个底面积相同的容器（质量与厚度不计）中分别装有深度和质量均相同的甲、乙、丙三种液体，则下列关于液体的密度ρ，液体对容器底的压力F，容器对桌面的压强p等关系正确的是（　　）

A．ρ甲＞ρ乙＞ρ丙 p甲＜p乙＜p丙
B．F甲＞F乙＞F丙 p甲＝p乙＝p丙
C．ρ甲＜ρ乙＜ρ丙 F甲＞F乙＞F丙
D．F甲＜F乙＜F丙 p甲＝p乙＝p丙
解：（1）由图可知，甲、乙、丙三种液体的体积关系是：V丙＞V乙＞V甲，
因为甲、乙、丙三种液体的质量相等，
所以，根据ρ=mV可知，甲、乙、丙三种液体的密度关系为：ρ甲＞ρ乙＞ρ丙，
（2）由图可知，甲容器上细下粗，液体对容器底的压力大于液体的重力；
乙容器为直壁容器，液体对容器底的压力等于液体的重力；
丙容器上粗下细，有一部分液体压在容器的侧壁上，液体对容器底的压力小于液体的重力，
甲、乙、丙三种液体的质量相等，则液体的重力相等，
所以，甲、乙、丙三种液体对容器底的压力关系为：F甲＞F乙＞F丙；
（3）三容器质量不计，容器内液体的质量相等，则重力相等，
容器对桌面的压力等于容器和液体的重力之和，
所以三容器对桌面的压力相等，且三个容器的底面积相同，
所以，根据p=FS可知，三容器对桌面的压强关系为：p甲＝p乙＝p丙；
故ACD错误，B正确。
答案：B。
9．在两个完全相同的容器中分别倒入甲和乙两种不同的液体，如图所示，下列分析正确的是（　　）

A．若甲和乙的质量相等，则甲的密度小于乙的密度
B．若甲和乙对容器底部的压强相等，则甲的密度小于乙的密度
C．若甲和乙对容器底部的压强相等，则甲的质量小于乙的质量
D．若甲和乙的质量相等，则甲对容器底部的压强小于乙对容器底部的压强
解：
A、由题意可知，甲和乙的质量相等，由图可知，V甲＜V乙，根据ρ=mV可知，ρ甲＞ρ乙，故A错误；
B、若甲和乙对容器底部的压强相等，由图可知，h甲＜h乙，根据p＝ρgh可知，ρ甲＞ρ乙，故B错误；
C、液体压强相等，两容器底面积相等，由p=FS可知，甲、乙对容器底的压力相等，即F甲＝F乙﹣﹣﹣﹣﹣﹣﹣﹣﹣①
采用割补法，分别把容器两侧半球部分补上同种液体，此时液体为圆柱形；
割补后深度不变，液体密度不变，所以液体对容器底的压强不变，又因为容器底面积不变，所以割补前后液体对容器底部的压力不变，且此时液体为圆柱形（液体对容器底的压力等于液体的总重力）；
所以，F甲＝G甲总﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②，F乙＝G乙总﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣③，
两容器完全相同，则补上的液体体积相等，设补充的液体体积为V，
由①②③可得：G甲总＝G乙总，
即m甲g+ρ甲gV＝m乙g+ρ乙gV﹣﹣﹣﹣﹣﹣﹣﹣④，
由B选项可知，ρ甲＞ρ乙；
所以由④式可得：m甲﹣m乙＝（ρ乙﹣ρ甲）V＜0，
所以m甲＜m乙，故C正确；
D、由A选项可知，ρ甲＞ρ乙，
由割补法可知，甲对容器底部的压力F甲＝m甲g+ρ甲gV，
乙对容器底部的压力F乙＝m乙g+ρ乙gV，
而m甲＝m乙，ρ甲＞ρ乙，
所以F甲＞F乙，
又因为两容器的底面积相等，所以根据公式p=FS可知，p甲＞p乙，故D错误。
答案：C。
10．如图所示，水平桌面上放有底面积和质量都相同的甲、乙两平底容器，分别装有深度相同、质量相等的不同液体。下列说法正确的是（　　）
①容器对桌面的压力：F甲＞F乙
②液体的密度：ρ甲＝ρ乙
③液体对容器底部的压强：p甲＞p乙
④容器对桌面的压强：p甲′＝p乙′

A．只有①和③ B．只有①和④ C．只有②和③ D．只有③和④
解：①水平桌面上，甲、乙两个容器中两种液体质量相等，则重力相等，容器底面积和质量相同，故对桌面的压力F甲＝F乙，由p=FS得，容器对桌面的压强：p甲′＝p乙′，故①错误，④正确；
②因为容器底面积相同，液体同高，乙中液体的体积大于甲中液体的体积，因为质量相同，所以ρ甲＞ρ乙，故②错误；
③由图知，两容器中液体的深度相同，由②知ρ甲＞ρ乙，根据p＝ρgh知，液体对杯底的压强p甲＞p乙；故③正确。
综上所述，①②错误，③④正确。
答案：D。
11．如图所示，完全相同的两个容器中分别装入甲、乙两种不同的液体，下列分析正确的是（　　）

A．若甲乙的质量相等，则A点的压强等于B点的压强
B．若甲乙的质量相等，则C点的压强小于D点的压强
C．若甲乙对容器底部的压强相等，若要使甲对容器底部的压强小于乙对容器底部的压强，可以在两容器中分别倒入体积相等的液体
D．若甲乙对容器底部的压强相等，则甲的质量一定大于乙的质量
解：
A、由图可知，甲、乙两容器内液体的体积关系为V甲液＞V乙液，因两容器中的液体质量相等，所以由m＝ρ液V可知，两容器内液体的密度关系为ρ甲液＜ρ乙液；
两容器完全相同，则容器中向外凸出部分的容积V凸相同，因ρ甲液＜ρ乙液，所以由G＝mg＝ρVg可知乙容器中凸出部分的液体重力较大，而两容器中液体的总重力相等，则两容器中柱形部分的液体重力G甲液′＞G乙液′，所以由F＝G柱液可知，两容器中液体对容器底部的压力F甲液＞F乙液；又因为两个容器完全相同，其底面积相同，所以由压强定义式可知，两液体对容器底部的压强p甲液＞p乙液﹣﹣﹣﹣﹣﹣﹣﹣①

由图可知，A、B两点到容器底部的距离相等，由p＝ρ液gh和ρ甲液＜ρ乙液可知，A、B两点到容器底部的压强关系为pA下＜pB下﹣﹣﹣﹣﹣﹣﹣﹣②；
因p甲液＞p乙液，所以，由pA上+pA下＞pB上+pB下可知，pA上＞pB上，即甲容器中液体对A点的压强大于乙容器中液体对B点的压强，故A错误；
B、由图可知，C、D两点到容器底部的距离相等，由p＝ρ液gh和ρ甲液＜ρ乙液可知，C、D两点到容器底部的压强关系为pC下＜pD下﹣﹣﹣﹣﹣﹣﹣﹣③；
因p甲液＞p乙液，所以，由pC上+pC下＞pD上+pD下可知，pC上＞pD上，即甲容器中液体对C点的压强大于乙容器中液体对D点的压强，故B错误；
C、若甲乙对容器底部的压强相等，由图可知，甲、乙两容器内液体的深度关系为h甲液＞h乙液，所以由p＝ρ液gh可知，两容器内液体的密度关系为ρ甲液＜ρ乙液，在两容器中分别倒入体积相等的液体，因两容器相同，则容器内液体升高的高度相等，即Δh甲＝Δh乙，由p＝ρ液gh和ρ甲液＜ρ乙液可知，两容器内液体对容器底部的压强增加量关系为Δp甲＜Δp乙，则甲对容器底部的压强小于乙对容器底部的压强，故C正确；
D、若甲乙对容器底部的压强相等，因两容器相同，由F＝pS知甲乙对容器底部的压力相等，则容器竖直方向上的甲的质量等于乙的质量，所以ρ甲＜ρ乙，即容器凸起部分的甲的质量小于乙的质量，所以总的甲的质量小于乙的总的质量，故D错误。
答案：C。
12．如图所示，两个完全相同的杯子置于水平桌面上，甲装密度为ρ1的液体，乙装密度为ρ2的液体，两杯子底部所受液体压强相等，甲杯中液体质量为M1，乙杯中液体质量为M2．当把小球A放在甲杯中时，有14体积露出液面，此时液体对容器底部的压强为P1；当把小球B放在乙杯中时，小球全部浸在液体中，此时液体对容器底部的压强为P2（两次液体均未溢出）。已知ρ1：ρ2＝5：4，两球体积相等。则下列判断正确的是（　　）

A．M1＞M2 P1＝P2 B．M1＜M2 P1＜P2
C．M1＝M2 P1＞P2 D．M1＜M2 P1＞P2
解：①根据题意可知，两杯子底部所受液体压强相等，即：p1＝p2，
若杯子为圆柱形，则根据G＝F＝ps可知，G1′＝G2′，
而由于杯子是如图所示形状，则甲、乙装的液体重力为：G1＝G1′﹣ΔG1′，G2＝G2′﹣ΔG2′；
因ΔG1′＝ρ1ΔV，ΔG2′＝ρ2ΔV；（ΔV为杯子凹进去的部分体积）
∵ρ1：ρ2＝5：4，即ρ1＞ρ2，
∴ΔG1′＞ΔG2′，
∴M1＜M2；
②当把小球A放在甲杯中时，有14体积露出液面，则液体对容器底部的压强p1＝ρ1g（h1+34VS），
当把小球B放在乙杯中时，小球全部浸在液体中，则液体对容器底部的压强p2＝ρ2g（h2+VS），
∴p1﹣p2＝ρ1g（h1+34VS）﹣ρ2g（h2+VS）
＝（ρ1gh1﹣ρ2gh2）+（ρ1g3V4S-ρ2gVS）
＝（ρ1gh1﹣ρ2gh2）+（34ρ1﹣ρ2）gVS
∵两杯子底部所受液体压强相等，则有ρ1gh1＝ρ2gh2；
∵ρ1：ρ2＝5：4，
∴ρ1=54ρ2，
∴34ρ1﹣ρ2=34×54ρ2﹣ρ2＝（1516--1）ρ2＜0，
∴p1﹣p2＜0，
即p1＜p2。
答案：B。
13．如图所示，盛有水的薄壁杯子静止在水平桌面上，杯子重为1N，高为9cm，底面积为30cm2；杯内水重为2N，水深为6cm，水的密度为1.0×103kg/m3，g取10N/kg。则：水杯对桌面的压力为　3　N，水对杯底的压强为　600　Pa，水对杯底的压力为　1.8　N。

解：水杯对桌面的压力：F＝G杯+G水＝1N+2N＝3N，
水对杯底的压强：p＝ρgh＝1.0×103kg/m3×10N/kg×0.06m＝600Pa；
由p=FS可得，水对杯底的压力：F＝pS＝600Pa×30×10﹣4m2＝1.8N。
答案：3；600；1.8。
14．将一未装满水的密闭矿泉水瓶，先正立放置在水平桌面上，再倒立放置，如图所示，则倒立时水对瓶盖的压强是 　1.2×103　Pa；正立时水对瓶底的压力为F1，倒立时水对瓶盖的压力为F2，则F1　＞　F2（选填“＞”、“＝”或“＜”）。

解：（1）由图可知，倒立时水的深度为h＝12cm＝0.12m，
则倒立时水对瓶盖的压强：p＝ρ水gh＝1.0×103kg/m3×10N/kg×0.12m＝1.2×103Pa；
（2）正放时，瓶子中的水柱是粗细相同的，瓶子底部受到的压力等于瓶中水的重力；倒放时，瓶子中的水柱上面粗，下面细，瓶盖受到的压力小于瓶中水的重力；瓶中水的重力是一定的，所以正放时水对瓶底的压力大于倒放时水对瓶盖的压力，即F1＞F2。
答案：1.2×103；＞。
15．如图所示，放在水平地面的容器，侧壁上有一开口弯管，弯管内的液面高度h1＝0.8m；其顶部和底部的面积均为0.1m2，顶部到底部的高度h2＝0.6m，容器中的液体密度为1.2×103kg/m3，则液体对容器顶部的压力为　240　N．（g＝10N/kg）

解：容器顶部到液面的距离h＝h2﹣h1＝0.8m﹣0.6m＝0.2m，
液体对容器顶部的压强P＝ρgh＝1.2×103kg/m3×10N/kg×0.2m＝2.4×103Pa，
液体对容器顶部的压力F＝PS＝2.4×103Pa×0.1m2＝240N。
答案：240。
16．如图所示，一装满水的密闭容器放置在水平桌面上，将其倒置后，水平桌面受到的压力将　不变　，水对容器底的压强将　不变　（均选填“变大”“变小”或“不变”）。

解：装满水的密闭容器放置在水平桌面上，其对水平桌面的压力等于容器和水的总重力，
将其倒置后，水的质量不变，容器和水的总重不变，
所以，水平桌面受到的压力将不变；
将其倒置后，水的深度不变，
根据p＝ρgh可知，水对容器底部的压强不变；
答案：不变；不变。
17．在两个完全相同的容器中分别倒入甲和乙两种不同的液体，如图所示，若甲和乙对容器底部的压强相等，则甲液体密度ρ1和乙液体ρ2的大小关系ρ1　＞　ρ2；甲液体质量m1和乙液体质量m2的大小关系m1　＜　m2（均填“＜”或“＞”或“＝”）。

解：因为甲和乙对容器底部的压强相等，所以p甲＝p乙；
由p＝ρgh可得，ρ甲gh甲＝ρ乙gh乙，而h甲＜h乙，所以ρ甲＞ρ乙；
因为容器完全相同，由F＝pS可得，ρ甲gh甲S＝ρ乙gh乙S；
如果容器为圆柱体，则ρ甲gh甲S＝ρ乙gh乙S⇒G甲＝G乙；
根据图示可知，两个容器相对于圆柱容器减少液体的体积相同，因此减小液体的重力关系：G甲′＝ρ甲gV，G乙′＝ρ乙gV
由于ρ甲＞ρ乙，所以G甲′＞G乙′；
则G甲﹣G甲′＜G乙﹣G乙′，即甲容器内液体甲的质量小于乙容器内液体乙的质量。
答案：＞；＜。
18．有一个重为G0牛顿的空心金属球用弹簧测力计吊着完全浸入一种密度为ρ1千克每立方米的液体中，此时弹簧测力计的示数为空心金属球重力的15，如图所示的另一容器，上部的横截面积为S1平方米，底部的横截面积为S2平方米，里面盛有密度为ρ2千克每立方米的另一种液体，ρ1：ρ2＝2：5，若把空心金属球放到这个容器的液体中待其静止后（容器足够大），液体对容器底部增加的压强为 　G0S1　Pa，液体对容器底部增加的压力为 　S2S1G0　N（g取10N/kg）。

解：空心金属球完全浸入一种密度为ρ1的液体中，球排开液体的体积等于球的体积V，
根据称重法可知：金属球受到的浮力F浮1＝G0-15G0=45G0，
由阿基米德原理可知：F浮1＝ρ1gV=45G0，
所以V=4G05ρ1g，
已知ρ1：ρ2＝2：5，
把金属球浸没放入第二种液体时，
它受到的浮力F浮′＝ρ2gV=52ρ1g×4G05ρ1g=2G0＞G0，
由此可见，金属球静止时将浮在液面上，它受到的浮力F浮2＝G0，即ρ2gV排2＝G0，
所以，V排2=G0ρ2g
液面上升的高度Δh=V排2S1=G0S1ρ2g；
放入金属球后，液体对容器底部增加的压强Δp＝ρ2gΔh＝ρ2gG0S1ρ2g=G0S1，
由p=FS得：
放入金属球后，容器底部所受液体的压力增大ΔF＝ΔpS2=S2S1G0。
答案：G0S1，S2S1G0。
19．如图甲所示的容器放置在水平地面上，该容器上、下两部分都是圆柱体，其横截面积分别为S1、S2，容器底部装有控制阀门。容器内装有密度为0.8×103kg/m3的液体，液体通过控制阀门匀速排出的过程中，容器底部受到液体的压强p随时间t变化关系如图乙所示。则阀门打开前液体的深度H＝　15　cm，上、下两部分横截面积之比S1：S2＝　1：4　。（g取10N/kg）

解：（1）由乙图可知，当t＝0s时，p＝1200Pa，
由p＝ρgh可得，阀门打开前液体的深度：H=pρg=1200Pa0.8×103kg/m3×10N/kg=0.15m＝15cm；
（2）设容器上面部分液体的高度为h1，h1对应的液体压强p1＝1200Pa﹣400Pa＝800Pa，
则h1=p1ρg=800Pa0.8×103kg/m3×10N/kg=0.1m＝10cm，
所以容器下面部分液体的高度为h2＝H﹣h1＝15cm﹣10cm＝5cm；
由于匀速排液，则后20s排出液体的体积是前10s排出液体体积的2倍，
由V＝Sh可得，上、下两部分液体的体积关系为：2S1h1＝S2h2，
则上、下两部分的横截面积之比为：S1S2=h22h1=5cm2×10cm=14。
答案：15；1：4。
20．如图所示，一只锥形烧瓶量得它的上口径与底径之比为1：3，放在水平桌面上，容器内有两种互不相溶的液体充满容器，且上、下两部分液体恰好深度相同。已知上、下两种液体的密度之比为ρ1：ρ2＝1：2，设上部液体对下部液体的压力为F1，下部液体对瓶底的压力为F2，则F1：F2＝　4：27　。

解：锥形烧瓶的上口径与底径之比r1：r2＝1：3，
则中间的口径r=r1+r22
故锥形烧瓶的中间的口径与底径之比：
r：r2=r1+r22：r2=r23+r22：r2＝2：3，
由S＝πr2得，锥形烧瓶的中间面积与底面积之比：
S：S2＝πr2：πr22=r2：r22=4：9，
由p＝ρgh得，上部液体对下部液体的压强：
p1＝ρ1gh，
下部部液体对瓶底的压强：
p2＝ρ1gh+ρ2gh，
由p=FS得，上部液体对下部液体的压力：
F1＝p1S＝ρ1ghS，
下部液体对瓶底的压力：
F2＝p2S＝（ρ1gh+ρ2gh）S2，
则F1F2=ρ1ghS(ρ1gh+ρ2gh)S2=ρ1S(ρ1+ρ2)S2=1×4(1+2)×9=427，
即：F1：F2＝4：27。
答案：4：27。