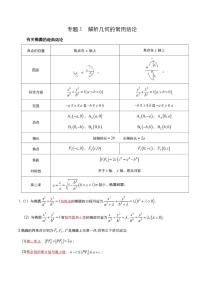































高考数学一轮复习之解析几何20讲
展开
这是一份高考数学一轮复习之解析几何20讲,文件包含1直线与方程doc、8中点弦问题--椭圆垂径定理doc、6椭圆的简单几何性质doc、16抛物线的焦点弦doc、3直线与圆的位置关系doc、10双曲线的标准方程doc、13双曲线的离心率计算doc、5椭圆的标准方程doc、18极点极线结构及非对称韦达定理doc、7直线与椭圆的位置关系及弦长计算doc、9椭圆离心率的计算doc、15抛物线的几何性质doc、14抛物线的标准方程doc、11双曲线的几何性质doc、2圆的标准方程与一般方程doc、20解析几何中的几何方法doc、17阿基米德三角形doc、4圆与圆的位置关系doc、12直线与双曲线的位置关系doc、19与斜率和斜率积有关的定点定值doc等20份试卷配套教学资源,其中试卷共94页, 欢迎下载使用。
课题1:直线与方程
第1课:倾斜角与斜率
一. 学习目标
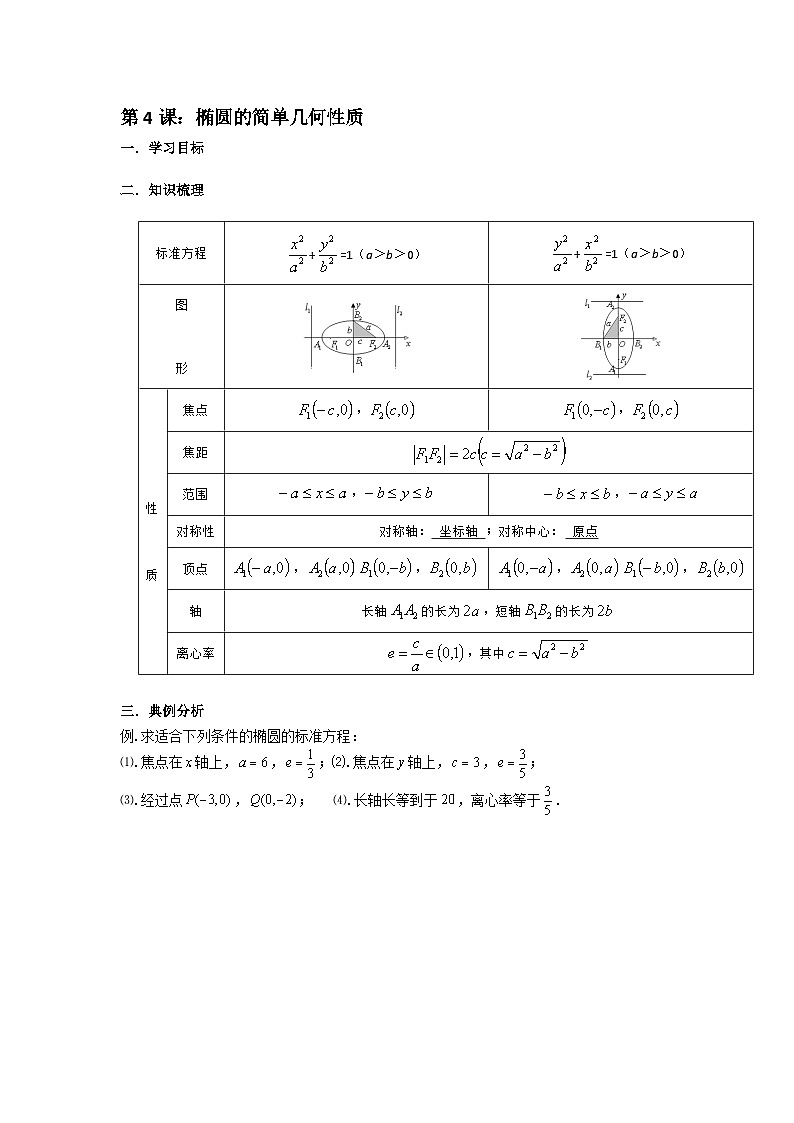
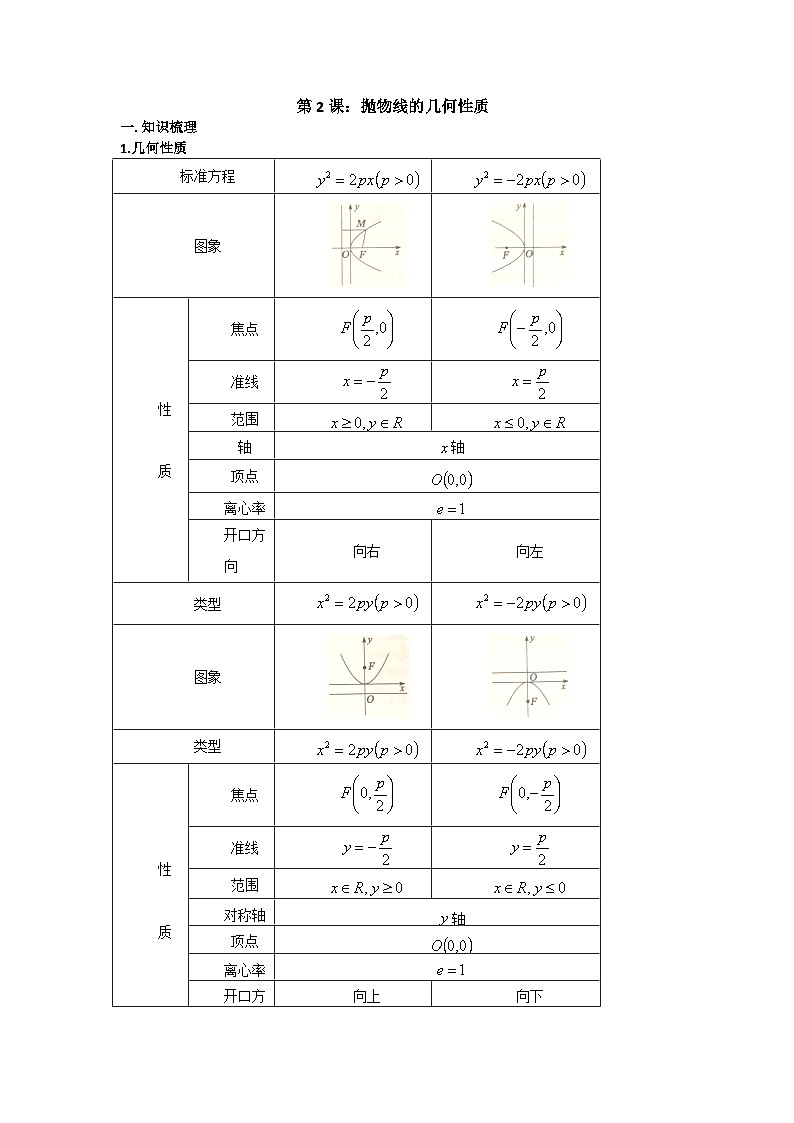
二.知识梳理:
(1)直线的倾斜角
定义:当直线与轴相交时,我们取轴作为基准,轴正向与直线向上方向之间所成的角叫做直线的倾斜角.
当直线与轴平行或重合时,规定它的倾斜角为.倾斜角的范围为.
(2)直线的斜率:
定义:一条直线的倾斜角的正切值叫做这条直线的斜率,斜率常用小写字母表示,即.
倾斜角是的直线,斜率不存在.
(3) 过两点的直线的斜率公式:
经过两点的直线的斜率公式:当时,;
当时,斜率不存在.
注:①任何直线都有倾斜角,但不是任何直线都有斜率,倾斜角是的直线的斜率不存在.
②斜率随倾斜角的变化规律:
倾斜角
斜率
,增大,增大
不存在
,增大,增大
③可以用斜率来证明三点共线,即若,则三点共线.
三.典例分析与练习题
1.在直角坐标系中,直线的倾斜角是( )
A.30° B.60° C.120° D.150°
2.若直线过点,则此直线的倾斜角是 ( )
A.30° B.45° C.60° D.90°
3.直线的倾斜角是().
A. B. C. D.
4.若三点在同一直线上,则实数等于( )
A. B.11 C. D.3
5.直线,的倾斜角是( )
A. B. C. D.
第2课:直线与方程
一.学习目标
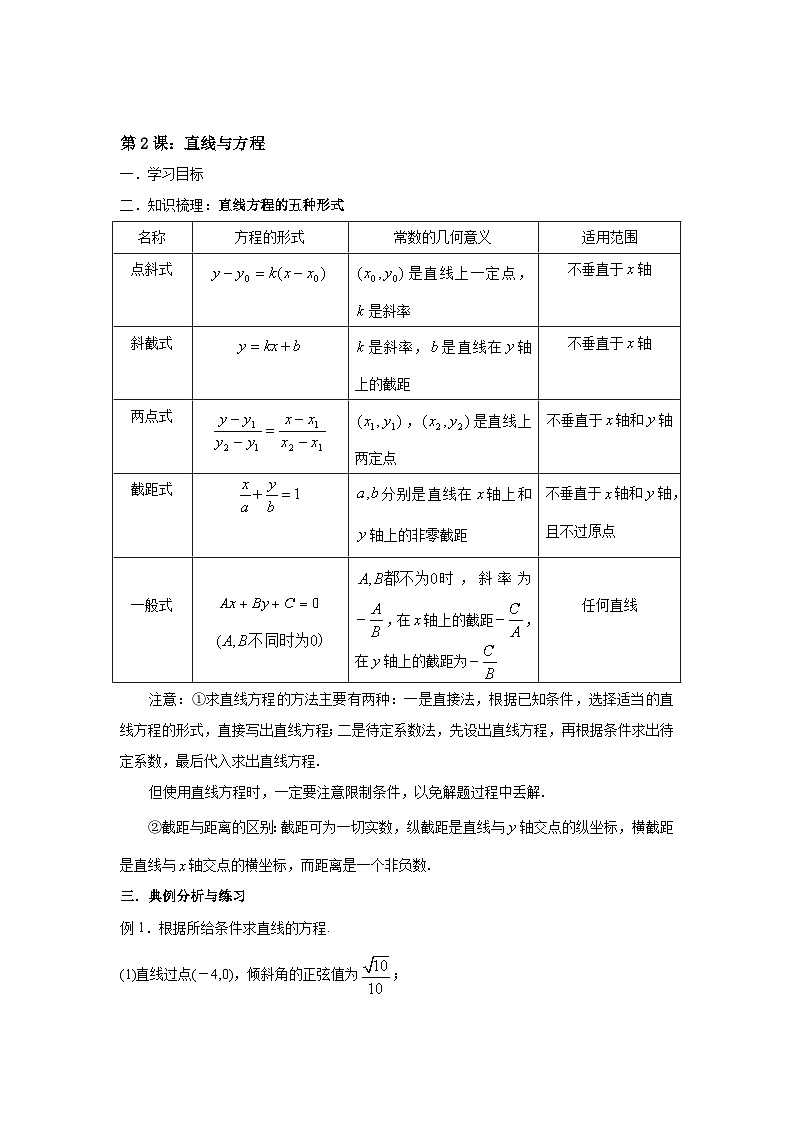
二.知识梳理:直线方程的五种形式
名称
方程的形式
常数的几何意义
适用范围
点斜式
是直线上一定点,是斜率
不垂直于轴
斜截式
是斜率,是直线在轴上的截距
不垂直于轴
两点式
,是直线上两定点
不垂直于轴和轴
截距式
分别是直线在轴上和轴上的非零截距
不垂直于轴和轴,且不过原点
一般式
时,斜率为,在轴上的截距,在轴上的截距为
任何直线
注意:①求直线方程的方法主要有两种:一是直接法,根据已知条件,选择适当的直线方程的形式,直接写出直线方程;二是待定系数法,先设出直线方程,再根据条件求出待定系数,最后代入求出直线方程.
但使用直线方程时,一定要注意限制条件,以免解题过程中丢解.
②截距与距离的区别:截距可为一切实数,纵截距是直线与轴交点的纵坐标,横截距是直线与轴交点的横坐标,而距离是一个非负数.
三.典例分析与练习
例1.根据所给条件求直线的方程.
(1)直线过点(-4,0),倾斜角的正弦值为;
(2)直线过点(-3,4),且在两坐标轴上的截距之和为12;
(3)直线过点(5,10),且到原点的距离为5.
例2.中,顶点,AC边所在直线方程为,AB边上的高所在直线方程为.
(1)求AB边所在直线的方程;
(2)求AC边的中线所在直线的方程.
四.练习题
1.经过点且在两坐标轴上截距相等的直线是( )
A. B. C.或 D.或
2.已知直线过点,且倾斜角为直线:的倾斜角的2倍,则直线的方程为( )
A. B.
C. D.
3.过点且与直线:平行的直线的方程是( )
A. B.
C. D.
4.已知中有,,且,则边上的中线所在直线方程为
A. B. C. D.
5.已知直线在两坐标轴上的截距相等,则实数
A.1 B. C.或1 D.2或1
6.无论 取何实数,直线恒过一定点,则该定点坐标为( )
A. B. C. D.
7.过点且在两坐标轴上截距相等的直线有( )
A.1条 B.2条 C.3条 D.4条
8.过点且与点距离最大的直线方程是()
A. B.
C. D.
9.点到直线(R)的距离的最大值为
A. B. C.2 D.
10.已知直线:.
(1)若直线不经过第四象限,求的取值范围;
(2)若直线交轴负半轴于点,交轴正半轴于点,为坐标原点,设的面积为4,求直线的方程.
第3课:直线与直线位置关系
一. 学习目标
二. 知识梳理
1.两条直线的交点
若直线:和:相交,则交点坐标是方程组的解.
2.两条直线位置关系的判定
(1)利用斜率判定
若直线和分别有斜截式方程:和:,则
①直线∥的等价条件为.
②直线与重合的等价条件为.
③直线与相交的等价条件为;特别地,的等价条件为.
若与斜率都不存在,则与平行或重合.
若与中的一条斜率不存在而另一条斜率为,则与垂直.
(2)用直线一般式方程的系数判定
设直线:,:,则
①直线∥的等价条件为.
②直线与重合的等价条件为.
③直线与相交的等价条件为;特别地, 的等价条件为
.
注:与平行的直线方程一般可设为的形式,与垂直的直线方程一般可设为的形式.
(3)用两直线联立的方程组的解的个数判定
设直线:,:,将这两条直线的方程联立,得方程组,若方程组有惟一解,则与相交,此解就是,交点的坐标;若方程组无解,此时与无公共点,则∥;若方程组有无数个解,则与重合.
3. 直线系问题
(1)设直线:和:
若与相交,则表示过与的交点的直线系(不包括);若∥,则上述形式的方程表示与与平行的直线系.
(2)过定点的旋转直线系方程为(不包括);斜率为的平行直线系方程为.
注:直线系是具有某一共同性质的直线的全体,巧妙地使用直线系,可以减少运算量,简化运算过程.
三.典例分析与练习
1.若直线与平行,则的值为( )
A.-1 B.1 C.-1或2 D.±1
2.设,则“”是“直线与直线平行”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知直线:,:,若,则( )
A. B.1 C.-1 D.不存在
4.已知直线:与:平行,则的值是( ).
A.或 B.或 C.或 D.或
5.已知直线:,:,:,若且,则的值为
A. B.10 C. D.2
6.已知直线,直线.
(1)若,求实数的值;
(2)若,求实数的值.
7.已知直线,与直线.
(1)若,求的值;
(2)若,求的值.
8.已知的顶点边上的中线所在直线方程为,边上的高所在直线方程为.求
(1)顶点的坐标;
(2)直线的方程.
9.已知中,,,,,垂足为.
(1)求直线的方程;
(2)求过点且平行于边的直线方程.
10.已知直线:,.
(1)证明:直线恒过定点;
(2)设是坐标原点,,若,求的值.
第4课:距离公式与对称问题
1.距离公式
(1)两点间的距离公式
平面上的两点间的距离.
特别地,原点与任一点的距离.
若轴时,;若轴时,.
(2)点到直线的距离公式
已知点,直线:,则点到直线的距离.
已知点,直线:,则点到直线的距离.
已知点,直线:,则点到直线的距离.
注:用此公式求解点到直线距离问题时,直线方程要化成一般式.
(3)两条平行直线间的距离公式
已知两平行直线:和:,若点在上,则两平行直线和的距离可转化为到直线的距离.
已知两平行直线:和:,则两直线和的距离.
注:用此公式求解两平行直线间的距离时,直线方程要化成一般式,并且项的系数必须对应相等.
2.对称问题
(1)中心对称
①点关于点的对称
点关于的对称点为.
②直线关于点的对称
在已知直线上取两点,利用中点坐标公式求出它们关于已知点对称的两点的坐标,再由两点式求出直线的方程,或者求出一个对称点,再利用∥,由点斜式求出直线的方程,或者在所求直线上任取一点,求出它关于已知点的对称点的坐标,代入已知直线,即可得到所求直线的方程.
(2)轴对称
①点关于直线的对称
点关于的对称点为,则有,由此可求出.
特别地, 点关于的对称点为,点关于的对称点为.
②直线关于直线的对称
此类问题一般转化为点关于直线的对称问题来解决,有两种情况:一是已知直线与对称直线相交,一是已知直线与对称直线平行.
三.典例分析与练习题
1.点关于直线对称的点的坐标是( )
A. B. C. D.
2.设直线 与直线的交点为,则到直线的距离最大值为( )
A. B. C. D.
3.已知直线(3k-1)x+(k+2)y-k=0,则当k变化时,所有直线都通过定点( )
A.(0,0) B.(,) C.(,) D.(,)
4.已知直线过定点,点在直线上,则的最小值是( )
A. B. C. D.
5.平行线与之间的距离等于( ).
A. B. C. D.
6.若点到直线的距离为1,则的值为( )
A. B. C.或 D.或
7.已知方程(2+λ)x-(1+λ)y-2(3+2λ)=0与点P(-2,2).
(1)证明:对任意的实数λ,该方程都表示直线,且这些直线都经过同一定点,并求出这一定点的坐标;
(2)证明:该方程表示的直线与点P的距离d小于.
8.已知直线l:x+2y-2=0.
(1)求直线l1:y=x-2关于直线l对称的直线l2的方程;
(2)求直线l关于点A(1,1)对称的直线方程.
9.已知直线l:3x-y+3=0,求:
(1)点P(4,5)关于l的对称点;
(2)直线x-y-2=0关于直线l对称的直线方程;
(3)直线l关于(1,2)的对称直线.
本章知识结构
直线的倾斜角和斜率
两条直线平行和垂直的判定
直线与方程
两条直线的位置关系
两条平行线间的距离
点到直线的距离
两点间的距离
相交求交点
平行求距离
直线的斜截式方程方程
直角坐标系中画图
直线的截距式方程
方程之间互化
直线的方程
直线的两点式方程
应用
直线的点斜式方程方程
直线的一般式方程方程
相关试卷
这是一份2024届高考第一轮复习:理科数学2010-2018高考真题分类训练之专题九 解析几何第二十六讲 椭圆,共14页。试卷主要包含了椭圆的离心率是,已知椭圆,已知O为坐标原点,F是椭圆C,设、是椭圆等内容,欢迎下载使用。
这是一份2024届高考数学第一轮复习:文科数学2010-2019高考真题分类训练之专题九 解析几何第二十五讲 椭圆,共18页。试卷主要包含了的焦点是椭圆的一个焦点,则p=,已知椭圆的右焦点为,且经过点.等内容,欢迎下载使用。
这是一份新高考数学二轮复习解析几何专题讲与练第20讲双曲线的离心率问题(教师版),共6页。