






- 人教版初中数学九年级上册22.1.3 第3课时《二次函数y=a(x-h)²+k的图象和性质》课件+教案+同步作业(含教学反思) 课件 2 次下载
- 人教版初中数学九年级上册22.1.4 第1课时《二次函数y=ax2+bx+c的图象和性质》课件+教案+同步作业(含教学反思) 课件 2 次下载
- 人教版初中数学九年级上册22.2《二次函数与一元二次方程》课件+教案+同步作业(含教学反思) 课件 2 次下载
- 人教版初中数学九年级上册22.3 第1课时《实际问题与二次函数——几何图形面积》课件+教案+同步作业(含教学反思) 课件 3 次下载
- 人教版初中数学九年级上册22.3 第2课时《实际问题与二次函数——商品利润》课件+教案+同步作业(含教学反思) 课件 3 次下载
初中人教版22.1.4 二次函数y=ax2+bx+c的图象和性质教学课件ppt
展开
第2课时 用待定系数法求二次函数的解析式 教学设计
![]()
二次函数是初中数学重要内容之一,而用待定系数法求函数解析式在前面的一次函数中已经多次运用,对本课时二次函数解析式的确定都很有帮助.教学中求函数的解析式,应恰当地选用函数解析式的形式,选择得当,解题简捷,若选择不当,解题繁琐.
![]()
课题 | 22.1.4第2课时用待定系数法求二次函数的解析式 | 授课人 |
|
素养目标 | 1.通过对用待定系数法求二次函数解析式的探究,掌握求解析式的方法. 2.在学习过程中,使学生亲自体会到学习数学知识的价值,会用数学的语言表达现实世界. | ||
教学重点 | 如何根据已知条件设恰当的函数解析式. | ||
教学难点 | 在实际问题中,体会二次函数作为一种数学模型的作用,会利用二次函数的性质求实际问题. | ||
授课类型 | 新授课 | 课时 |
|
![]()
教学步骤 | 师生活动 | 设计意图 |
复习回顾 | 1.求下列函数的解析式: (1)一个正比例函数的图象经过点(3,-7); (2)一个一次函数的图象与x轴交于点(3,0),与y轴交于点(0,6). 2.用待定系数法求函数解析式的基本步骤有哪些? 3.学习过的二次函数的解析式有哪些? 师生活动:学生独立完成并进行口述,教师对学生的解答情况进行评价并总结: 用待定系数法求函数解析式的步骤:设出解析式、列出方程(组)、解方程(组)、代入. 二次函数的解析式: 一般式:y=ax2+bx+c; 顶点式:y=a(x-h)2+k. | 在学生解决问题的基础上进一步体会知识,为后面的学习做好铺垫. |
活动一:创设情境、导入新课 | 【课堂引入】 问题:已知一个二次函数的图象经过(-1,10),(1,4),(2,7)三点,求这个函数的解析式. 师生活动:学生感知问题,独立思考. | 通过问题设疑,引导学生进入本课时的学习. |
活动二:实践探究、交流新知 | 【探究新知】 活动一:针对【课堂引入】的问题进行探究: 师生活动:学生独立思考问题,教师提示设出合适的函数解析式,学生自主进行解答,教师做好辅导工作. 学生分析问题:根据图象经过三个点,可设二次函数的一般式,再把三个点的坐标代入后解三元一次方程组即可. 教师展示学生作业,然后展示正确答案. 解:设二次函数的解析式为y=ax2+bx+c(a≠0). 将三点坐标分别代入,得解得 所以这个二次函数的解析式为y=2x2-3x+5. 活动二:已知抛物线的顶点坐标为(-1,-3),与y轴的交点为(0,-5),求这个抛物线的函数解析式. 师生活动:教师指导学生根据例1的解答过程和步骤,运用类比的思想方法解答此题. 学生独立进行解答,教师做好点拨和引导,帮助学生正确解答问题. 学生分析问题:根据已知抛物线的顶点坐标,可设函数解析式为y=a(x-h)2+k,把顶点坐标代入后,再把另一点的坐标代入求出a的值即可. 解:设这个抛物线的函数解析式为y=a(x+1)2-3. 因为点(0,-5)在抛物线上,所以a-3=-5,解得a=-2. 所以这个抛物线的函数解析式为y=-2(x+1)2-3. 化成一般式为y=-2x2-4x-5. 2.归纳总结 请学生以小组为单位,讨论总结求二次函数解析式的思路和方法,并讲给大家听. 师生活动:教师选派个别学生回答,其他同学进行补充,教师订正、总结: (1)已知图象上三个点或三对x,y的值,通常选择一般式:y=ax2+bx+c,把条件代入得到三元一次方程组,解方程组即可; (2)已知图象的顶点和对称轴,通常选择顶点式:y=a(x-h)2+k,先把顶点坐标代入,再把另一点的坐标代入求出a的值,最后化为一般式即可. | 1.运用类比的思想方法,用待定系数法求二次函数的解析式.已知抛物线上三个点的坐标,运用一般式求解. 2.在给定顶点坐标时,设一般式求解较麻烦,所以引导学生采用顶点式解答,这样让学生了解对于不同类型的问题有不同的解答方案,有利于活跃学生的思维,养成善于总结的习惯. |
活动三:开放训练、体现应用 | 【典型例题】 例 已知抛物线的顶点坐标为(20,16),且经过点(0,0),(40,0).求抛物线的函数解析式. 师生活动:教师选派两名同学选择不同的解答方式进行板演,其他同学在练习本上书写解答过程,教师做好指导和评价. 解法1:设抛物线的函数解析式为y=ax2+bx+c. 由抛物线经过(0,0),(20,16),(40,0)三点,可得 解得 所以抛物线的函数解析式为y=-x2+x. 教师评价:利用给定的条件列出关于a,b,c的三元一次方程组,求出a,b,c的值,从而确定函数的解析式. 解法2:设抛物线的函数解析式为y=a(x-20)2+16. 因为点(0,0)在抛物线上, 所以0=400a+16, 解得a=-. 所以抛物线的函数解析式为y=-(x-20)2+16, 即y=-x2+x. 教师评价:已知抛物线的顶点,选用顶点式求抛物线的函数解析式. 【变式训练】 已知抛物线与x轴交于点A(-1,0),B(1,0)并经过点M(0,1),求此抛物线的解析式. 提示:当抛物线与x轴有两个交点为(x1,0),(x2,0)时,二次函数y=ax2+bx+c可以转化为交点式y=a(x-x1)(x-x2).因此当抛物线与x轴有两个交点为(x1,0),(x2,0)时,可设二次函数的解析式为y=a(x-x1)(x-x2),再把另一个点的坐标代入其中,即可解得a,求出抛物线的解析式. 解:因为抛物线与x轴的交点为A(-1,0),B(1,0),所以设抛物线的解析式为y=a(x+1)(x-1). 又因为点M(0,1)在抛物线上, 所以a(0+1)(0-1)=1,解得a=-1. 故抛物线解析式为y=-(x+1)(x-1),即y=-x2+1. | 通过课前设疑,激发学生的学习兴趣,运用所学知识,从不同的角度进行解答,既训练了学生一题多解的能力和思维的灵活性,又培养了学生深层次的思维能力. |
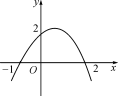
活动四:课堂检测 | 【课堂检测】 1.已知抛物线y=ax2+bx+c过(1,0),(2,0),(3,4)三点,则该抛物线的解析式为(B) A.y=x2-3x+2 B.y=2x2-6x+4 C.y=2x2-6x-4 D.y=x2-3x-2 2.如图,抛物线的解析式为(D)
A.y=-x2-x+2 B.y=x2+x+2 C.y=-2x2+x+2 D.y=-x2+x+2 3.已知二次函数的图象的顶点是(1,-2),且经过点(0,-5),则二次函数的解析式是(C) A.y=-3(x+1)2-2 B.y=3(x+1)2-2 C.y=-3(x-1)2-2 D.y=3(x-1)2-2 4.已知二次函数y=ax2+bx+c,当x=0时,y=1;当x=-1时,y=6;当x=1时,y=0.求这个二次函数的解析式. 解:由题意,得解得 ∴二次函数的解析式为y=2x2-3x+1. | 针对本课时的主要问题,从多个角度、分层次进行检测,达到学有所成、了解课堂学习效果的目的. |
课堂小结 | 1.课堂小结: 你在本节课中有哪些收获?有哪些进步?还有哪些困惑?请谈一谈. 教师强调:用待定系数法求函数解析式的两种类型:已知三点坐标用一般式,已知顶点坐标用顶点式. 2.布置作业: 教材第42页习题22.1第10(2)(4),11题. | 学生归纳本节课学习的主要内容,让学生自觉对所学知识进行梳理,形成体系,养成良好的学习习惯.布置作业体现分层教学,加深认识、深化提高,形成体系. |
板书设计 | 22.1.4.2 用待定系数法求二次函数的解析式 1.已知图象上三点求二次函数的解析式 2.已知顶点求二次函数的解析式 | 提纲挈领,重点突出. |
教学反思 | 本课时的主要内容是利用待定系数法求二次函数解析式,教师应让学生体会求解过程,关键是让学生学会如何运用三点式,顶点式,交点式等来求解析式. | 反思教学过程和教师表现,进一步优化操作流程和提升自身素质. |
初中数学人教版九年级上册22.1.4 二次函数y=ax2+bx+c的图象和性质教课ppt课件: 这是一份初中数学人教版九年级上册22.1.4 二次函数y=ax2+bx+c的图象和性质教课ppt课件,共29页。PPT课件主要包含了xh时y最大k,−20,直线x−2,填一填,x−62,x−62−36,练一练,−15,x0时yc,直线x1等内容,欢迎下载使用。
数学九年级上册22.1.4 二次函数y=ax2+bx+c的图象和性质习题课件ppt: 这是一份数学九年级上册22.1.4 二次函数y=ax2+bx+c的图象和性质习题课件ppt,共23页。PPT课件主要包含了y1<y2,y=x-32+2等内容,欢迎下载使用。
2020-2021学年22.1.4 二次函数y=ax2+bx+c的图象和性质课文ppt课件: 这是一份2020-2021学年22.1.4 二次函数y=ax2+bx+c的图象和性质课文ppt课件,共18页。PPT课件主要包含了配方可得,描点画图,试一试,你知道吗,用配方法,要记住公式哦,我来模仿,小试牛刀等内容,欢迎下载使用。