新教材2023高中数学第八章立体几何初步8.4空间点直线平面之间的位置关系8.4.1平面分层演练新人教A版必修第二册

这是一份新教材2023高中数学第八章立体几何初步8.4空间点直线平面之间的位置关系8.4.1平面分层演练新人教A版必修第二册，共3页。
8.4 空间点、直线、平面之间的位置关系 8.4.1 平面A级　基础巩固1.下列图形中,不一定是平面图形的是 (　　)A.三角形B.菱形C.梯形D.四条边相等的四边形解析:三角形的三个顶点为不共线的三点,因此一定是平面图形;菱形、梯形分别有两组、一组对边平行,故为平面图形;四边相等的四边形可能为空间四边形.答案:D2.已知点A,直线a,平面α,以下命题表述正确的个数是 (　　)①A∈a,a∈α⇒A∈α;②A∉a,a⊂α⇒A∉α;③A∈a,a⊂α⇒A⊂α.A.0　　　　B.1　　　　C.2　　　　D.3解析:①不正确,因为“a∈α”表述错误;②不正确,如图所示,A∉a,a⊂α,但A∈α;③不正确,“A⊂α”表述错误.答案:A3.已知α,β为平面,A,B,M,N为点,a为直线,下列推理错误的是 (　　)A.A∈a,A∈β,B∈a,B∈β⇒a⊂βB.M∈α,M∈β,N∈α,N∈β⇒α∩β=MNC.A∈α,A∈β⇒α∩β=AD.A,B,M∈α,A,B,M∈β,且A,B,M不共线⇒α,β重合解析:因为A∈α,A∈β,所以A∈α∩β. 由基本事实可知α∩β为经过A的一条直线而不是A. 故α∩β=A的写法错误.答案:C4.空间内两两平行的三条直线最多可以确定　　　　个平面. 解析:如图所示,此时确定的平面个数最多.答案:35.如图所示,在四面体A-BCD中作截面PQR,若PQ,CB的延长线交于点M,RQ,DB的延长线交于点N,RP,DC的延长线交于点K.求证:M,N,K三点共线.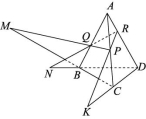证明:因为M∈PQ,PQ⊂平面PQR,M∈BC,BC⊂平面BCD,所以M是平面PQR与平面BCD的一个公共点,所以点M在平面PQR与平面BCD的交线上.同理可证,点N,K也在平面PQR与平面BCD的交线上.所以M,N,K三点共线.B级　能力提升6.已知空间四点中,任何三点都不共线,则经过其中三点的平面有 (　　)A.1个 B.4个C.1个或4个 D.无法确定解析:第一种情况,四点共面,则有一个平面,第二种情况,四点不共面,因为任何三点都不共线,则任何三点都确定一个平面,所以可以有4个,故选C.答案:C7.在空间四边形ABCD中,在AB,BC,CD,DA上分别取E,F,G,H四点,如果GH,EF交于一点P,则 (　　)A.点P一定在直线BD上B.点P一定在直线AC上C.点P在直线AC或BD上D.点P既不在直线BD上,也不在直线AC上解析:由题意知,GH⊂平面ADC.因为GH,EF交于一点P,所以P∈平面ADC.同理,P∈平面ABC.因为平面ABC∩平面ADC=AC,由基本事实3可知点P一定在直线AC上.答案:B8.若平面α与平面β、平面γ都相交,则这三个平面可能的交线有　　　　条. 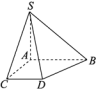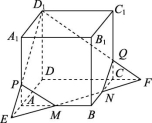解析:当平面β与平面γ相交时,若平面α过平面β与平面γ的交线,则这三个平面有1条交线;若平面α不过平面β与平面γ的交线,则这三个平面有3条交线;当平面β与平面γ平行时,则这三个平面有2条交线.答案:1或2或3 9.如图所示,在直角梯形ABDC中,AB∥CD,AB>CD,S是直角梯形ABDC所在平面外一点,画出平面SBD和平面SAC的交线.解:点S是平面SBD和平面SAC的一个公共点,即点S在这两个平面的交线上.由于AB>CD,则分别延长AC和BD交于点E,如图所示.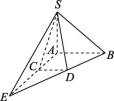因为E∈AC,AC⊂平面SAC,所以E∈平面SAC.同理,可证E∈平面SBD,所以点E在平面SBD和平面SAC的交线上,则连接SE,直线SE就是平面SBD和平面SAC的交线.C级　挑战创新10.如图所示,正方体木料ABCD-A1B1C1D1,其中M,N分别是AB,CB的中点,要过D1,M,N三点将木料锯开,请你帮助木工师傅想办法,怎样画线才能顺利完成?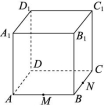解:作法如下:(1)连接MN并延长交DC的延长线于点F,连接D1F交CC1于点Q,连接QN;(2)延长NM交DA的延长线于点E,连接D1E交AA1于点P,连接MP;(3)依次在正方体各个面上画线D1P,PM,MN,NQ,QD1,即为木工师傅所要画的线.