数学选择性必修 第三册6.1 分类加法计数原理与分步乘法计数原理第2课时习题

这是一份数学选择性必修 第三册6.1 分类加法计数原理与分步乘法计数原理第2课时习题，共5页。
6.1 分类加法计数原理与分步乘法计数原理 第2课时 两个计数原理的综合应用A级　基础巩固1.某乒乓球队里有6名男队员,5名女队员,从中选取男队员、女队员各1名组成混合双打队,则不同的组队方法的种数为(　　)A.11B.30C.56D.65解析:先选1名男队员,有6种方法,再选1名女队员,有5种方法,故共有6×5=30种不同的组队方法.答案:B2.由数字1,2,3,4组成的三位数中,各位数字按严格递增(如“134”)或严格递减(如“421”)顺序排列的数的个数是(　　)A.4B.8C.16D.24解析:由题意,知严格递增的三位数只要从4个数中任取3个,共有4种取法;同理,严格递减的三位数也有4个,所以符合条件的数的个数为4+4=8.答案:B3.如图,一只蚂蚁从点A出发沿着水平面的线条爬行到点C,再由点C沿着置于水平面的长方体的棱爬行至顶点B,则它可以爬行的不同的最短路径有(　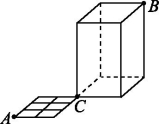　)A.40条B.60条C.80条D.120条解析:蚂蚁从A到C需要走五段路,其中三纵二横,共有10条路径,从C到B共有6条路径,根据分步乘法计数原理可知,蚂蚁从A到B可以爬行的不同的最短路径的条数为10×6=60.答案:B4.如图,给A,B,C,D四块区域涂色,要求相邻区域涂不同颜色,现有5种不同颜色可供选用,则不同的涂色方法有320种.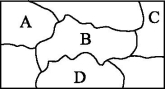解析:由题意,知本题是一个分步乘法计数问题,第一步,涂A,有5种涂法;第二步,涂B,有4种涂法;第三步,涂C,有4种涂法;第四步,涂D,有4种涂法,则不同的涂色方法的种数为5×4×4×4=320.5.多空题由1,2,3,4,5,6,7,8,9可以组成224个无重复数字的三位偶数,可以组成280个无重复数字的三位奇数.解析:当个位上的数是偶数时,该三位数就是偶数.可分步完成:第一步,先排个位,个位上的数只能取2,4,6,8中的 1个,有4种取法;第二步,排十位,从剩余的8个数字中取1个,有8种取法;第三步,排百位,从剩余的7个数字中取1个,有7种取法.所以可以组成无重复数字的三位偶数的个数为4×8×7=224.当个位上的数是奇数时,该三位数就是奇数.可分步完成:第一步,先排个位,个位上的数只能取1,3,5,7,9中的1个,有5种取法;第二步,排十位,从剩余的8个数字中取1个,有8种取法;第三步,排百位,从剩余的7个数字中取1个,有7种取法.所以可以组成无重复数字的三位奇数的个数为5×8×7=280.6.(2022·上海卷)用数字1、2、3、4组成没有重复数字的四位数,则这些四位数中比2 134大的数字个数为17.(用数字作答)解析:根据题意,用数字1、2、3、4组成没有重复数字的四位数,当其千位数字为3或4时,有2×3×2×1=12种情况,即有12个符合题意的四位数;当千位数字为2时,有3×2=6个四位数,其中最小的为2 134,则有6-1=5个比 2 134 大的四位数,故有12+5=17个比2 134大的四位数.7.某外语组有9人,每人至少会英语和日语中的一种,其中7人会英语,3人会日语,从中选出会英语和会日语的各一人,有多少种不同的选法?解:完成一件事指“从9人中选出会英语和会日语的各一人”,故需分三类:①既会英语又会日语的当选;②仅会英语不会日语的按会英语当选;③仅会日语不会英语的按会日语当选.既会英语又会日语的人数为7+3-9=1,仅会英语的有6人,仅会日语的有2人.先分类后分步,从仅会英语、仅会日语的人中各选一人,有6×2种选法; 从仅会英语与英语、日语都会的人中各选一人,有6×1种选法;从仅会日语与英语、日语都会的人中各选一人,有2×1种选法.根据分类加法计数原理,知共有6×2+6×1+2×1=20种不同的选法.B级　拓展提高8.从1,3,5,7,9这五个数字中,每次取出两个不同的数字分别作为a,b,共可得到lg a-lg b的不同值的个数是(　　)A.9B.10C.18D.20解析:分两步完成,第一步,取数字a,有5种不同的取法;第二步,取数字b,有4种不同的取法,所以可以得到5×4=20个不同的减法算式.因为lg 9-lg 3=lg 3-lg 1,lg 3-lg 9=lg 1-lg 3,所以lg a-lg b的不同值的个数是20-2=18. 答案:C9.现有1元、5元、10元、50元人民币各一张,100元人民币2张,从中至少取一张,共可组成不同的币值种数是47种.解析:除100元人民币以外每张均有取和不取2种情况,2张100元人民币的取法有不取、取一张和取两张3种情况,再减去这些人民币全不取的1种情况,所以共有 24×3-1=47种.10.某校学生会由高一年级5人,高二年级6人,高三年级4人组成.(1)选其中1人为学生会主席,有多少种不同的选法?(2)若每个年级选1人为校学生会常委,有多少种不同的选法?(3)若要从不同的两个年级中各选1人参加市里组织的活动,有多少种不同的选法?解:(1)根据分类加法计数原理,不同选法的种数为5+6+4=15.(2)根据分步乘法计数原理,不同选法的种数为5×6×4=120.(3)要选出不同年级的2人参加市里组织的活动,先按年级分三类:“高一、高二年级”“高一、高三年级”“高二、高三年级”,再分步选择,则不同选法的种数为5×6+5×4+6×4=74.C级　挑战创新11.多选题几只猴子在一棵枯树上玩耍,假设它们均不慎失足下落,已知(1)猴子甲在下落的过程中依次撞击到树枝A,B,C;(2)猴子乙在下落的过程中依次撞击到树枝D,E,F;(3)猴子丙在下落的过程中依次撞击到树枝G,A,C;(4)猴子丁在下落的过程中依次撞击到树枝B,D,H;(5)猴子戊在下落的过程中依次撞击到树枝I,C,E.下列结论正确的是(　　)A.最高处的树枝为G,I当中的一个B.最低处的树枝一定是FC.这九根树枝从高到低不同的顺序共有33种D.这九根树枝从高到低不同的顺序共有32种解析:由题判断出部分树枝由高到低的顺序为GABCEF,还剩下D,H,I,且树枝I比C高,树枝D在树枝B,E之间,树枝H比D低,故A选项正确.先看树枝I,有4种可能,若I在B,C之间,则D有3种可能:当D在B,I 之间时,H有5种可能;当D在I,C之间时,H有4种可能;当D在C,E之间时,H有3种可能,此时树枝的高低顺序有5+4+3=12种.若I不在B,C之间,则I有3种可能,D有2种可能:当D在B,C之间时,H有4种可能,当D在C,E之间时,H有3种可能,此时树枝的高低顺序有3×(4+3)=21种.故这九根树枝从高到低不同的顺序共有12+21=33种,故C选项正确.故选AC.答案:AC12.多空题用1,2,3,4四个数字组成可有重复数字的三位数,这些数从小到大构成数列{an},则这个数列共有64项;若an=341,则n=45.解析:由题意,知这个数列的项数就是由1,2,3,4四个数字组成的可有重复数字的三位数的个数.由于每个数位上的数都有4种取法,由分步乘法计数原理,得满足条件的三位数的个数为4×4×4=64,即数列{an}共有64项.比341小的数分为两类:第一类,百位上的数是1或2,有2×4×4=32个三位数;第二类,百位上的数是3,十位上的数可以是1,2,3中的任意一个,个位上的数可以是1,2,3,4中的任意一个,有3×4=12个三位数.所以比341小的三位数的个数为32+12=44,因此,341是数列{an}的第45项,即n=45.13.多空题用n种不同颜色给下列两块广告牌涂色(如图①、图②),要求a,b,c,d四个区域中相邻(有公共边)的区域不能用同一种颜色.　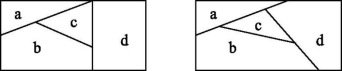　　　图①图②若n=6,为图①涂色,共有480种不同的方法;为图②涂色时共有120种不同方法,则n=5.解析:对于题图①,因为a,d只与周围两个区域相邻,而b,c与周围三个区域相邻.分两类情况:①a,d同色,a,d有n种不同的涂色方法,则b,c有(n-1)(n-2)种不同的涂色方法,共有n(n-1)(n-2)种不同的涂色方法.②a,d不同色,则a,d有n(n-1)种不同的涂色方法,b,c有(n-2)(n-3)种不同的涂色方法,共有n(n-1)(n-2)(n-3)种不同的涂色方法.故共有n(n-1)(n-2)+n(n-1)(n-2)(n-3)=n(n-1)(n-2)(n-2)种不同的涂色方法.当n=6时,共有480种不同的涂色方法.对于题图②,共有n(n-1)(n-2)(n-3)种不同的涂色方法.由n(n-1)(n-2)(n-3)=120,可得n=5.