初中数学冀教版八年级下册22.4 矩形作业ppt课件

这是一份初中数学冀教版八年级下册22.4 矩形作业ppt课件，共24页。
1. 如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.求证:四边形ABCD是矩形.
1.证明:∵AO=CO,BO=DO,∴四边形ABCD是平行四边形,∴∠ABC=∠ADC.∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形.
知识点1 有一个角是直角的平行四边形是矩形
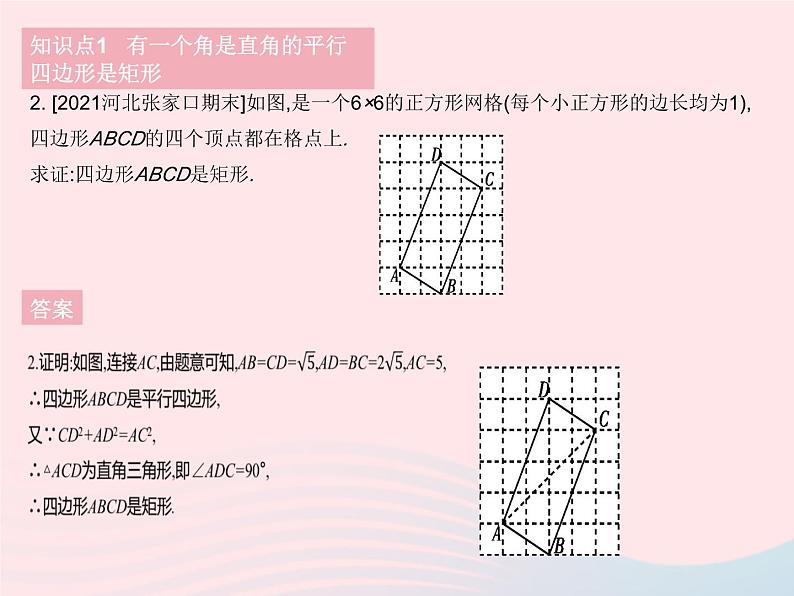
2. [2021河北张家口期末]如图,是一个6×6的正方形网格(每个小正方形的边长均为1),四边形ABCD的四个顶点都在格点上.求证:四边形ABCD是矩形.
3. [2021河北唐山月考]如图,在四边形ABCD中,AB∥CD,∠C=90°.若再添加一个条件,就能推出四边形ABCD是矩形,则添加的条件是　　　　　　　　.(写出一种情况即可) 
3.∠A=90°(或∠D=90°或AB=CD或AD∥BC)(答案不唯一)　∵AB∥CD,∠C=90°,∴∠B=90°.根据有三个角是直角的四边形是矩形,可知只需添加条件∠A=90°或∠D=90°即可;根据有一个角是直角的平行四边形是矩形,可知只需添加条件AB=CD或AD∥BC即可.
知识点2 有三个角是直角的四边形是矩形
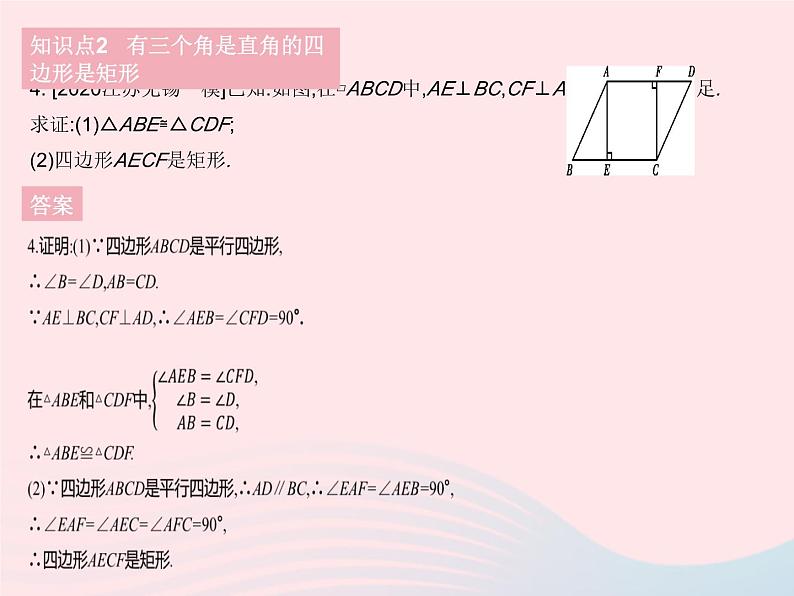
4. [2020江苏无锡一模]已知:如图,在▱ABCD中,AE⊥BC,CF⊥AD,E,F分别为垂足.求证:(1)△ABE≌△CDF;(2)四边形AECF是矩形.
5. [教材P139练习T2变式]如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.(1)求证:△ABD≌△CAE.(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.
6. [2021河北沧州期末]在数学活动课上,老师让同学们判断一个四边形门框是否为矩形,下面是某合作小组的四位同学的拟订方案,其中正确的是 (　　)A.测量对角线是否互相平分B.测量两组对边是否分别相等C.测量一组对角是否为直角D.测量两组对边是否分别相等,再测量对角线是否相等
6.D　A项,对角线互相平分的四边形是平行四边形,故A错误;B项,两组对边分别相等的四边形是平行四边形,故B错误;C项,根据一组对角为直角无法判断四边形的形状,故C错误;D项,两组对边分别相等的四边形是平行四边形,对角线相等的平行四边形是矩形,故D正确.
知识点3 对角线相等的平行四边形是矩形
7. 如图,在四边形ABCD中,对角线AC,BD相交于点O,AB∥CD且AB=CD,∠BAC=∠BDC.求证:四边形ABCD是矩形.
7.证明:∵AB∥CD且AB=CD,∴四边形ABCD是平行四边形,∠ABD=∠BDC,∴AC=2OA,BD=2OB.∵∠BAC=∠BDC,∴∠ABD=∠BAC,∴OA=OB,∴AC=BD,∴四边形ABCD是矩形.
8. [2021河北石家庄外国语学校期末]如图,在△AEC,△BED中,∠AEC=∠BED=90°,AC,BD相交于点O,且O是AC,BD的中点.求证:四边形ABCD是矩形.
1. [2021广西梧州中考]如图,在Rt△ABC中,点D,E,F分别是边AB,AC,BC的中点,AC=8,BC=6,则四边形CEDF的面积是 (　　)A.6B.12C.24 D.48
3. 如图,在四边形ABCD中,∠A=60°,∠ABC=∠ADC=90°,BC=2,CD=11,过点D作DH⊥AB于点H,则DH的长是 (　　)A.7.5B.7C.6.5D.5.5
4. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,且OA=OB,∠OAD=55°,则∠ODC的度数为　　　　. 
4.35°　∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.∵OA=OB,∴OA=OB=OC=OD,∴AC=BD,∴四边形ABCD是矩形,∴∠ADC=90°.∵∠ODA=∠OAD=55°,∴∠ODC=∠ADC-∠ODA=35°.
5. [2020北京顺义区一模]如图,将一矩形纸片ABCD沿着虚线EF剪成两个全等的四边形纸片,则剪得的四边形纸片中较短的边AE的长是　　　　. 
6. [2021河北张家口期末]如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF长的最小值是　　　　. 
7. [2021广西河池期末]如图,平行四边形ABCD的两条对角线交于点O,△AOB是等边三角形.(1)求证:四边形ABCD是矩形.(2)若OE⊥BD交BC于点E,CE=2,求AD的长.
7.(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.∵△AOB是等边三角形,∴OA=OB=AB,∴OA=OC=OB=OD,∴AC=BD,∴四边形ABCD是矩形.
(2)解:∵四边形ABCD是矩形,∴OB=OC,∠ABC=90°.∵△AOB是等边三角形,∴∠ABO=60°,∴∠OBC=∠OCB=30°,∴∠BOC=120°.∵BD⊥OE,∴∠BOE=90°,∴BE=2OE,∠EOC=30°,∴∠EOC=∠ECO,∴OE=CE,∴BE=2OE=2CE=4,∴AD=BC=BE+CE=6.
8. 原创题已知▱ABCD和▱GBEF是全等形,∠ABC=60°.(1)如图1,当点F与点D重合时,BG交AD于点M,EF交BC于点N.求证:BM=DM.(2)将▱GBEF绕点B旋转,当GF和DC互相垂直时,如图2,求∠GBC的度数.(3)将图2中的▱GBEF绕点B逆时针旋转90°,则以点C,G,D,F为顶点的四边形是哪种特殊四边形?请给予证明.
(3)解:以点C,G,D,F为顶点的四边形是矩形.证明如下:如图,旋转后点E与点A重合,∠GBC=60°+60°=120°.∵BG=BC,∴∠BGC=∠BCG=30°,∴∠GCD=120°-30°=90°.∵四边形ABCD和四边形GBEF是平行四边形,∴AB∥CD,AB∥FG,AB=CD,AB=FG,∴FG∥CD,FG=CD,∴四边形CDFG是平行四边形,又∵∠GCD=90°,∴四边形CDFG是矩形.