2023八年级数学下册第二十二章四边形全章综合检测作业课件新版冀教版

这是一份2023八年级数学下册第二十二章四边形全章综合检测作业课件新版冀教版，共31页。

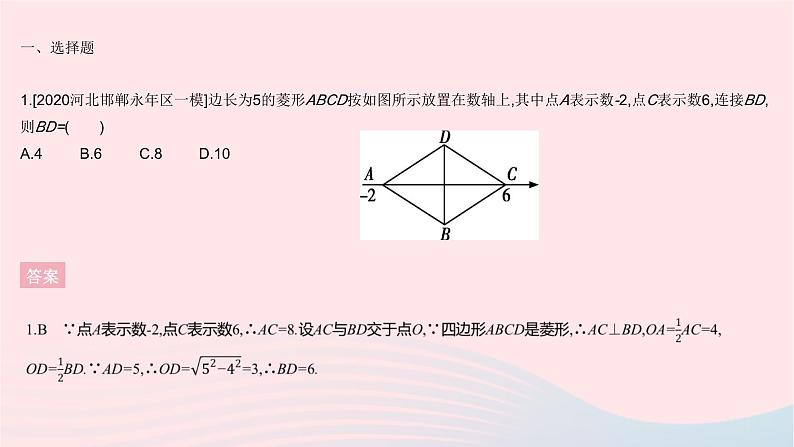
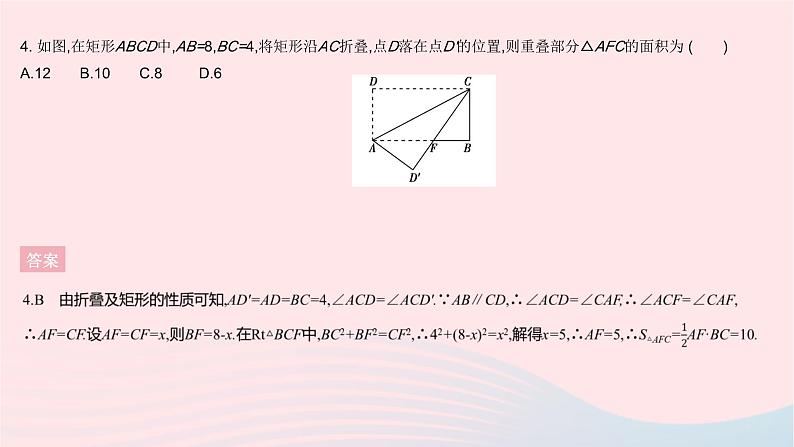
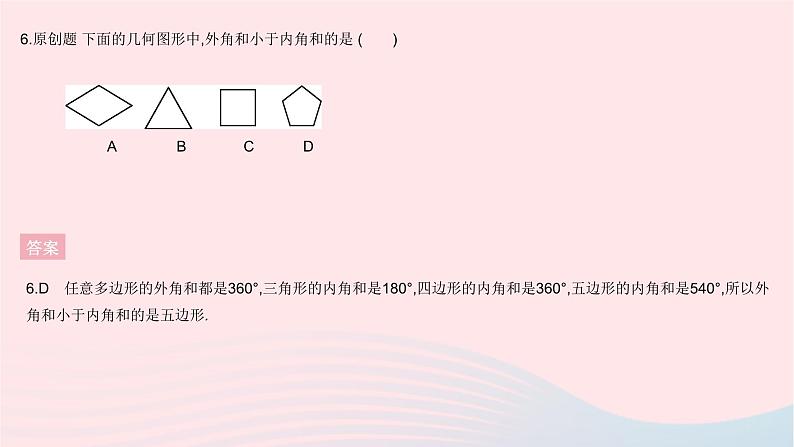
全章综合检测一、选择题　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　1.[2020河北邯郸永年区一模]边长为5的菱形ABCD按如图所示放置在数轴上,其中点A表示数-2,点C表示数6,连接BD,则BD=(　　)A.4 B.6 C.8 D.10答案  答案2.B　根据“连接三角形两边中点的线段叫做三角形的中位线”,可知①代表中位线;根据三角形的中位线定理“三角形的中位线平行于第三边,并且等于第三边的一半”,可知②代表DE∥AC;根据推理过程可知DF∥AC,DF=AC,故③代表一组对边平行且相等.3 平面直角坐标系中,已知平行四边形ABCD的其中三个顶点的坐标分别是A(m,n),B(-2,1),C(-m,-n),则点D的坐标是 (　　)A.(2,-1) B.(-2,-1)C.(-1,2) D.(-1,-2)答案3.A　∵A(m,n),C(-m,-n),∴点A和点C关于原点对称.∵四边形ABCD是平行四边形,∴点D和点B关于原点对称.∵B(-2,1),∴点D的坐标是(2,-1).4. 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D'的位置,则重叠部分△AFC的面积为 (　　)A.12 B.10 C.8 D.6答案 5.如图,在平行四边形ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠C的度数是 (　　)A.115° B.105° C.75° D.65°答案5.A　∵四边形AEFG是正方形,∴∠AEF=90°.∵四边形ABCD是平行四边形,∴AD∥BC,∠C=∠BAD,∴∠EAD=180°-∠AEC=180°-90°-15°=75°,∴∠BAD=40°+75°=115°,∴∠C=115°.6.原创题 下面的几何图形中,外角和小于内角和的是 (　　)　　　 A　　　　B　　　 C　　 　D答案6.D　任意多边形的外角和都是360°,三角形的内角和是180°,四边形的内角和是360°,五边形的内角和是540°,所以外角和小于内角和的是五边形. 7. [2021河北保定期末]如图,▱ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为 (　　)A.15 B.18 C.21 D.24答案  答案8.B　∵四边形APCD和四边形PBEF都是正方形,∴AP=CP,PF=PB,∠APF=∠BPC=∠PBE=90°,∴△AFP≌△CBP(SAS),∴∠AFP=∠CBP,又∵∠CBE=α ,∴∠AFP=∠CBP=∠PBE-∠CBE=90°-α.9.[2020江苏无锡期中]如图,菱形ABCD的边长为5,对角线AC的长为8,延长AB至点E,BF平分∠CBE,点G是BF上任意一点,则△ACG的面积为(　　)答案 10.[2020广东广州白云区模拟]如图,过▱ABCD的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于点E,F,G,H,则下列说法错误的是(　　)A.EH=GH B.AC与EG互相平分C.EH∥FG D.AC平分∠DAB答案  答案  答案 二、填空题13.[2021江苏苏州期末]“花影遮墙,峰峦叠窗”,苏州园林空透的窗棂中蕴含着许多的数学元素.如图1,2分别是冰裂纹窗窗棂和这种窗棂中的部分图案.若∠1=∠2=75°,∠3=∠4=65°,则∠5=　　　　　. 答案13.80°　由多边形的外角和为360°,可得∠5=360°-∠1-∠2-∠3-∠4=80°.14.[2021山东烟台期中]如图,四边形ABCD是菱形,点O是对角线的交点,三条直线都经过点O,图中阴影部分的面积为24 cm2,其中一条对角线长为6 cm,则另一条对角线长为　　　　cm. 答案14.16　由阴影部分的面积为24 cm2,易知菱形的面积为48 cm2,因为菱形的一条对角线长为6 cm,所以菱形的另一条对角线长为48÷6×2=16(cm).15.[2020山东枣庄中考]如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是　　　　. 答案 16.[2021河北唐山期末]在平面直角坐标系xOy中,已知四边形ABCD是平行四边形,且点A(0,-2),B(m,m+1),C(6,2).(1)线段AC的中点E的坐标为　　　　; (2)对角线BD长的最小值为　　　　. 答案 三、解答题17.[2021河北邯郸期末]如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.(1)求证:四边形AFHD为平行四边形.(2)若CB=CE,∠BAE=70°,∠DCE=20°,求∠CBE的度数. 答案18.[2020山东菏泽期中]已知:如图,在四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且AE=CE.(1)求证:四边形ABCD是菱形.(2)如果BE=BC,且∠CBE∶∠BCE=2∶3.求证:四边形ABCD是正方形.答案 (2)∵BE=BC,∴∠BCE=∠BEC.设∠BCE=∠BEC=3x°,则∠CBE=2x°.根据三角形内角和定理,得2x°+3x°+3x°=180°,解得x=22.5,∴∠CBE=45°.∵△ABD≌△CBD,∴∠ABE=∠CBE=45°,∴∠ABC=90°,又∵四边形ABCD是菱形,∴四边形ABCD是正方形.答案19.[2020北京中考]如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.(1)求证:四边形OEFG是矩形.(2)若AD=10,EF=4,求OE和BG的长.答案19.(1)证明:∵四边形ABCD为菱形,∴点O为BD的中点,又∵点E为AD的中点,∴OE为△ABD的中位线,∴OE∥FG,又∵OG∥EF,∴四边形OEFG为平行四边形,又∵EF⊥AB,∴四边形OEFG为矩形. 答案20.如图1,在正方形ABCD中,点E为AB上的点(不与A,B重合),△ADE与△FDE关于DE对称,作射线CF,与DE的延长线相交于点G,连接AG.(1)当∠ADE=15°时,求∠DGC的度数;(2)若点E在AB上移动,请你判断∠DGC的度数是否发生变化,若不变化,请证明你的结论,若发生变化,请说明理由;(3)如图2,点F在对角线BD上,点M为DE的中点,连接AM,FM,请判断四边形AGFM的形状,并证明结论.答案20.解:(1)∵∠ADE=15°,∴∠FDE=15°,∴∠CDF=60°.由对称可知AD=DF,∴DF=DC,∴△DFC是等边三角形,∴∠CFD=60°.∵∠CFD=∠DGC+∠FDE=∠DGC+15°,∴∠DGC=45°.  答案 21.[2021河北石家庄新华区期末]如图,在平面直角坐标系中,O为坐标原点,四边形OABC为矩形,A(0,5),C(26,0).点E是OC的中点,动点M在线段AB上以每秒2个单位长度的速度由点A向点B运动(到点B时停止).设动点M的运动时间为t秒.(1)当t为何值时,四边形MOEB是平行四边形?(2)若四边形MOEB是平行四边形,请判断四边形MAOE的形状,并说明理由.(3)在线段AB上是否存在一点N,使得以O,E,M,N为顶点的四边形是菱形?若存在,求出t的值;若不存在,请说明理由.21.解:(1)如图1,∵四边形OABC为矩形,C(26,0),∴OC=AB=26,OC∥AB.∵点E是OC的中点,∴OE=CE=13.∵四边形MOEB是平行四边形,∴BM=OE=13,∴AM=26-13=13.∵动点M的速度为每秒2个单位长度,∴t=13÷2=6.5.(2)四边形MAOE是矩形.理由如下:如图2,由(1)可知AM=OE=13,AM∥OE,∴四边形MAOE是平行四边形,∵∠AOE=90°,∴四边形MAOE是矩形.答案 答案