2023八年级数学下册第二十二章四边形易错疑难集训二作业课件新版冀教版

这是一份2023八年级数学下册第二十二章四边形易错疑难集训二作业课件新版冀教版，共13页。

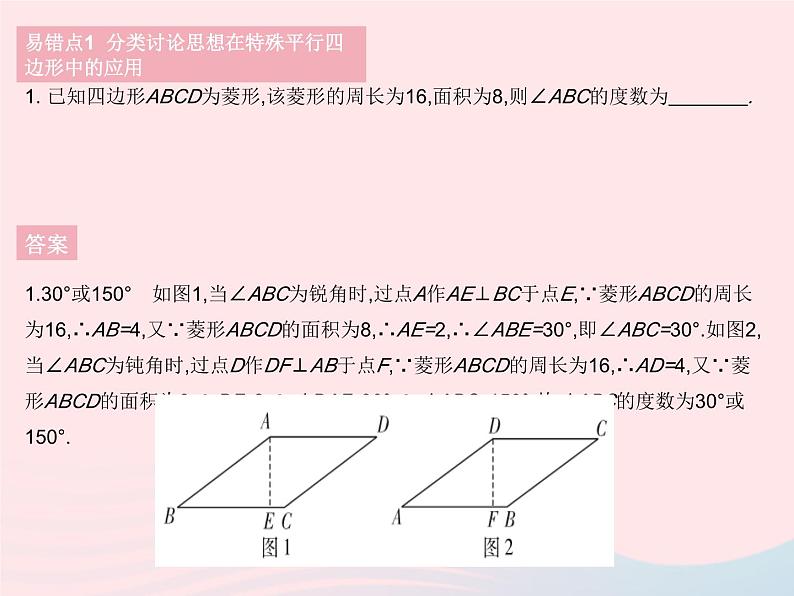
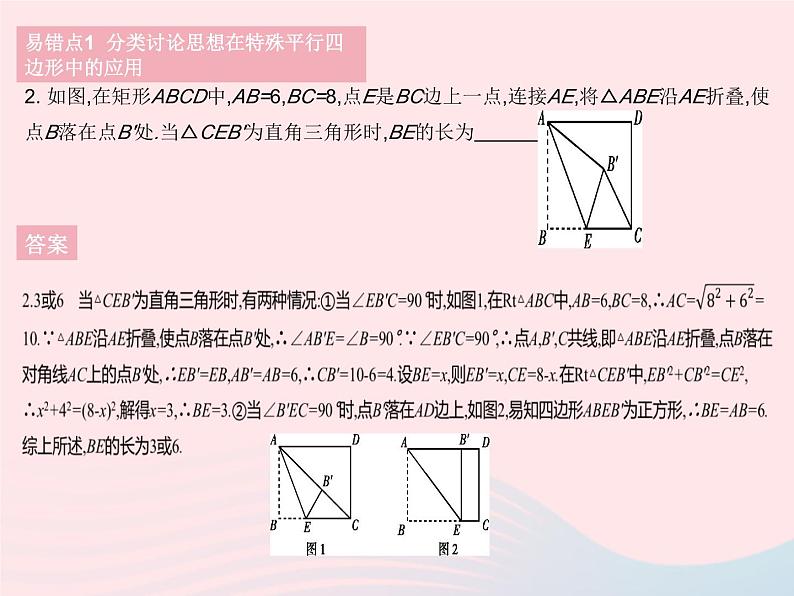
易错疑难集训（二）1. 已知四边形ABCD为菱形,该菱形的周长为16,面积为8,则∠ABC的度数为　　　　. 答案1.30°或150°　如图1,当∠ABC为锐角时,过点A作AE⊥BC于点E,∵菱形ABCD的周长为16,∴AB=4,又∵菱形ABCD的面积为8,∴AE=2,∴∠ABE=30°,即∠ABC=30°.如图2,当∠ABC为钝角时,过点D作DF⊥AB于点F,∵菱形ABCD的周长为16,∴AD=4,又∵菱形ABCD的面积为8,∴DF=2,∴∠DAF=30°,∴∠ABC=150°.故∠ABC的度数为30°或150°.易错点1 分类讨论思想在特殊平行四边形中的应用2. 如图,在矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,将△ABE沿AE折叠,使点B落在点B'处.当△CEB'为直角三角形时,BE的长为　　　　. 答案 易错点1 分类讨论思想在特殊平行四边形中的应用3 .给出下列结论:①对角线相等的四边形是矩形;②对角线互相垂直的四边形是菱形;③对角线互相垂直的矩形是正方形.其中,正确的有(　　)A.0个 B.1个 C.2个 D.3个 答案3.B　对角线相等的平行四边形是矩形,故①错误;对角线互相垂直的平行四边形是菱形,故②错误;对角线互相垂直的矩形是正方形,故③正确.易错点2 混淆特殊平行四边形的判定4.如图1,将矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.(1)求证:△BDF是等腰三角形.(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.①判断四边形BGDF的形状,并说明理由;②若AB=6,AD=8,求FG的长.　 图1　　　　　　　　图2 易错点2 混淆特殊平行四边形的判定答案 1. [2020黑龙江哈尔滨期中]如图,在四边形ABCD中,对角线 AC⊥BD,垂足为点O,点E,F,G,H分别为边AD,AB,BC,CD 的中点.若AC=8,BD=6,则四边形EFGH的面积为　　　　.  疑难点　“中点”四边形问题答案 2 在平行四边形ABCD中,AC,BD交于点O,过点O作直线EF,GH,分别交平行四边形的四条边于E,F,G,H四点,连接EG,GF,FH,HE.(1)如图1,试判断四边形EGFH的形状,并说明理由;(2)如图2,当EF⊥GH时,四边形EGFH的形状是　　　　　; (3)如图3,在(2)的条件下,若AC=BD,则四边形EGFH的形状是　　　　　; (4)如图4,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.疑难点　“中点”四边形问题答案2.分析:“中点”四边形的形状是由原四边形的两条对角线的数量关系和位置关系决定的.首先,不管原四边形的形状怎样改变,“中点”四边形始终是平行四边形;其次,具体的“中点”四边形形状的确定还需参考原四边形具备的其他条件,内容如下表:解:(1)四边形EGFH是平行四边形.理由如下:∵平行四边形ABCD的对角线AC,BD交于点O,∴点O是平行四边形ABCD的对称中心,∴EO=FO,GO=HO,∴四边形EGFH是平行四边形.答案(2)菱形(3)菱形(4)四边形EGFH是正方形.理由如下:∵AC=BD,∴平行四边形ABCD是矩形,∴OA=OB=OC,又∵AC⊥BD,∴∠BOC=90°,∠GBO=∠FCO=45°.∵EF⊥GH,∴∠GOF=90°,∴∠BOG=∠COF,∴△BOG≌△COF,∴OG=OF,∴GH=EF.由(3)知四边形EGFH是菱形,又∵GH=EF,∴四边形EGFH是正方形.