2023八年级数学下册第二十二章四边形热门考点集训作业课件新版冀教版

这是一份2023八年级数学下册第二十二章四边形热门考点集训作业课件新版冀教版，共14页。

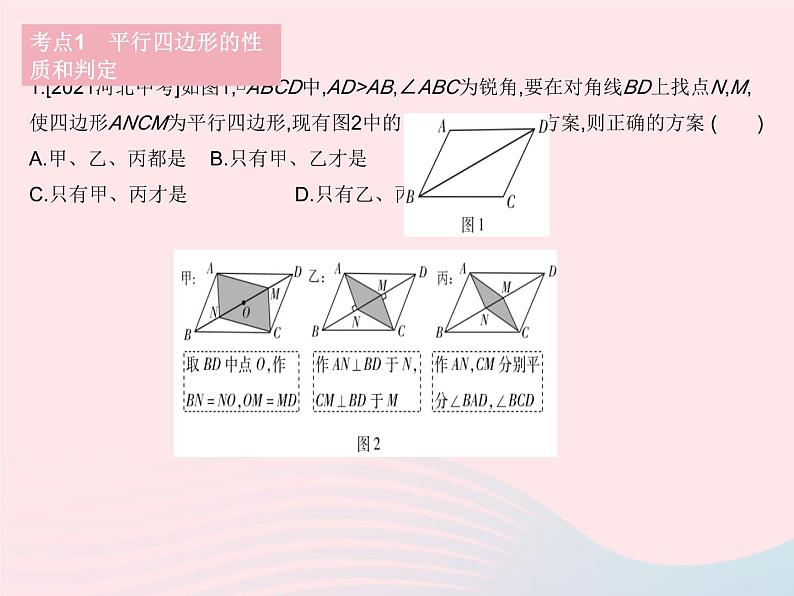
河北热门考点集训1.[2021河北中考]如图1,▱ABCD中,AD>AB,∠ABC为锐角,要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案 (　　)A.甲、乙、丙都是 B.只有甲、乙才是C.只有甲、丙才是 D.只有乙、丙才是 考点1　平行四边形的性质和判定答案1.A　对于甲方案,连接AC,∵四边形ABCD是平行四边形,∴AC经过BD的中点O,且AO=CO,又∵BO=DO,BN=NO,OM=MD,∴NO=OM,∴四边形ANCM是平行四边形(对角线互相平分的四边形是平行四边形).对于乙方案,易证△ABN≌△CDM,∴AN=CM.∵AN⊥BD,CM⊥BD,∴AN∥CM,∴四边形ANCM是平行四边形(一组对边平行且相等的四边形是平行四边形).对于丙方案,易证△BAN≌△DCM,∴AN=CM,∠ANB=∠CMD,∴∠ANM=∠CMN,∴AN∥CM,∴四边形ANCM是平行四边形(一组对边平行且相等的四边形是平行四边形).综上可知,甲、乙、丙三种方案都是正确的.考点1　平行四边形的性质和判定 答案 考点1　平行四边形的性质和判定3.[2021河北唐山路南区期中]如图,在四边形ABCD中,AB∥DC,AD=BC=6,DC=9,AB=15,点P从点A出发以每秒2个单位长度的速度沿AD→DC向终点C运动,同时点Q从点B出发,以每秒1个单位长度的速度沿BA向终点A运动.当有一点到达终点时,另一点也停止运动.当运动时间为　　　　s时,四边形PQBC为平行四边形. 答案3.5　当四边形PQBC为平行四边形时,CP∥BQ且CP=BQ,易知此时点P在线段DC上.设运动时间为t s,则CP=15-2t,BQ=t,所以15-2t=t,所以t=5.故当运动时间为5 s时,四边形PQBC为平行四边形.考点1　平行四边形的性质和判定4.[2021河北唐山二模]如图,点B,F,C,E在直线l上,点A,D在l异侧,AB∥DE,AB=DE,BF=EC.(1)求证:△ABC≌△DEF.(2)连接AF,CD,判断四边形AFDC的形状,并说明理由.答案4.(1)证明:∵AB∥DE,∴∠ABC=∠DEF.∵BF=EC,∴BF+FC=EC+FC,即BC=EF,又∵AB=DE,∴△ABC≌△DEF.(2)解:四边形AFDC为平行四边形.理由如下:∵△ABC≌△DEF,∴AC=DF,∠ACB=∠DFE,∴AC∥DF,∴四边形AFDC为平行四边形.考点1　平行四边形的性质和判定5.[2021河北唐山期中]在“类比探究菱形的有关问题”这节网课中,老师给出了如下画菱形的步骤,请问这样画的依据是 (　　)A.四条边都相等的四边形是菱形B.两组对边分别相等的四边形是平行四边形,有一组邻边相等的平行四边形是菱形C.两组对边分别平行的四边形是平行四边形,有一组邻边相等的平行四边形是菱形D.两组对边分别平行的四边形是平行四边形,两条对角线互相垂直的平行四边形是菱形答案5.C　由作图的第一步可知AD=AB,由作图的第二步可知CD∥AB,由作图的第三步可知AD∥BC,所以四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形),因为AD=AB,所以四边形ABCD是菱形(有一组邻边相等的平行四边形是菱形).考点2　特殊平行四边形的性质和判定6.[2021河北唐山路南区二模]如图,将矩形ABCD绕点A顺时针旋转α(0°<α<360°),得到矩形AEFG.当GB=GC时,α的度数为 (　　)A.60°或300° B.60°或330°C.30° D.60°答案6.A　分两种情况讨论:①如图1,当点G在AD右侧时,取BC的中点H,连接GH交AD于M,连接GD,∵GB=GC,∴GH⊥BC.∵四边形ABCD为矩形,∴AD∥BC,AD=BC,∴GM垂直平分AD,∴GD=GA=DA,∴△ADG是等边三角形,∴∠DAG=60°,∴旋转角α=60°.②如图2,当点G在AD左侧时,同理可得△ADG是等边三角形,∴∠DAG=60°,∴旋转角α=360°-60°=300°. 图1 图2考点2　特殊平行四边形的性质和判定7.[2021河北邯郸三模]现有一张纸片,∠BAF=∠B=∠D=∠FED=∠F=90°,AB=AF=2,EF=ED=1.有甲、乙两种剪拼方案,如图1,2所示,将它们沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则 (　　)A.甲、乙都不可以B.甲不可以,乙可以C.甲、乙都可以D.甲可以,乙不可以答案7.C　如图1,将△AEF移至①处,△DEH移至②处,四边形GCHE移至③处,即可得到一个与原来面积相等的正方形;如图2,将△ABG,△AHG,△HGF分别移至①②③处,即可得到一个与原来面积相等的正方形,所以甲、乙方案都可以.考点2　特殊平行四边形的性质和判定8.[2021河北张家口期末]已知:如图,在▱ABCD中,G,H分别是AD,BC的中点,E,O,F是对角线BD上的四等分点,顺次连接GE,EH,HF,FG.(1)求证:四边形GEHF是平行四边形.(2)当▱ABCD满足　　　　时,四边形GEHF是菱形. (3)若BD=2AB,①探究四边形GEHF的形状,并说明理由.②当AB=2,∠ABD=120°时,直接写出四边形GEHF的面积.考点2　特殊平行四边形的性质和判定答案 考点2　特殊平行四边形的性质和判定答案 考点2　特殊平行四边形的性质和判定答案 考点2　特殊平行四边形的性质和判定