初中数学华师大版八年级下册第19章 矩形、菱形与正方形19.2 菱形1. 菱形的性质作业课件ppt

这是一份初中数学华师大版八年级下册第19章 矩形、菱形与正方形19.2 菱形1. 菱形的性质作业课件ppt，共27页。

1. 原创题 如图,以▱ABCD的顶点A为圆心、边AD的长为半径画弧交边AB于点E,过点E作EF∥AD交边DC于点F,则四边形AEFD是　　　　. 
知识点1 菱形的定义
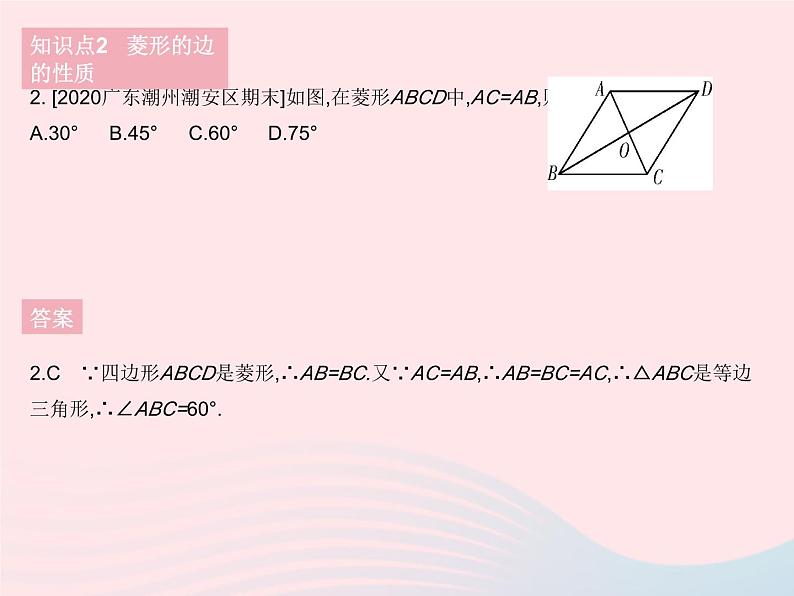
2. [2020广东潮州潮安区期末]如图,在菱形ABCD中,AC=AB,则∠ABC= (　　)A.30°B.45°C.60°D.75°
知识点2 菱形的边的性质
2.C　∵四边形ABCD是菱形,∴AB=BC.又∵AC=AB,∴AB=BC=AC,∴△ABC是等边三角形,∴∠ABC=60°.
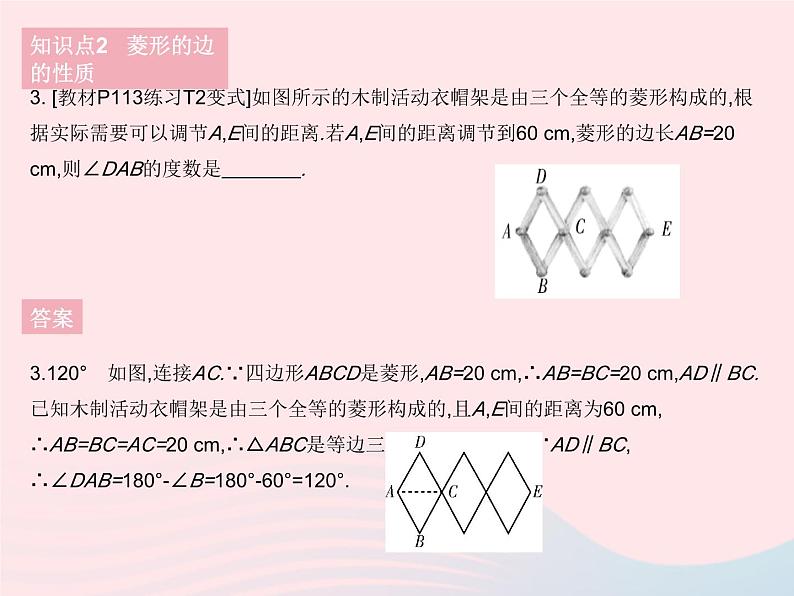
3. [教材P113练习T2变式]如图所示的木制活动衣帽架是由三个全等的菱形构成的,根据实际需要可以调节A,E间的距离.若A,E间的距离调节到60 cm,菱形的边长AB=20 cm,则∠DAB的度数是　　　　. 
3.120°　如图,连接AC.∵四边形ABCD是菱形,AB=20 cm,∴AB=BC=20 cm,AD∥BC. 已知木制活动衣帽架是由三个全等的菱形构成的,且A,E间的距离为60 cm, ∴AB=BC=AC=20 cm,∴△ABC是等边三角形,∴∠B=60°.∵AD∥BC,∴∠DAB=180°-∠B=180°-60°=120°.
4. [2021四川广安中考]如图,四边形ABCD是菱形,点E,F分别在边AB,AD的延长线上,且BE=DF,连接CE,CF.求证:CE=CF.
5. [2020浙江宁波北仑区期末]在平面直角坐标系中,菱形ABCD的顶点A,B,C的坐标分别为(-2,0),(0,1),(2,0),则顶点D的坐标为 (　　)A.(0,-1)B.(-2,1)C.(2,1)D.(0,-2)
知识点3 菱形的对角线的性质
5.A　如图,∵菱形ABCD的对角线互相垂直平分,顶点A,B,C的坐标分别为(-2,0),(0,1),(2,0),∴顶点D的坐标为(0,-1).
6. [教材P112练习T1变式][2021江苏南通中考]菱形的两条对角线的长分别是6和8,则这个菱形的周长是 (　　)A.24B.20C.10D.5
7. [2020山东济南期末]如图,在菱形ABCD中,点E是AB边上的一点,连接DE交AC于点O,连接BO,且∠AED=50°,则∠CBO=　　　　°. 
7.50　∵四边形ABCD是菱形,∴AB∥CD,CD=CB,∠BCO=∠DCO,∴∠CDO=∠AED=50°.易证△BCO≌△DCO,∴∠CBO=∠CDO=50°.
8. 如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.(1)求证:AE=EC.(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.
知识点4 菱形的面积
10. 一个菱形的边长为6,面积为28,则该菱形的两条对角线的长度之和为　　　　. 
2. 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,交AB于点E,连接DF,则∠CDF等于(　　)A.50°B.60°C.70°D.80°
3. [2021浙江绍兴中考]如图,菱形ABCD中,∠B=60°,点P从点B出发,沿折线BCD移动,移动到点D停止.在△ABP形状的变化过程中,依次出现的特殊三角形是 (　　)A.直角三角形→等边三角形→等腰三角形→直角三角形B.直角三角形→等腰三角形→直角三角形→等边三角形C.直角三角形→等边三角形→直角三角形→等腰三角形D.等腰三角形→等边三角形→直角三角形→等腰三角形
3.C　当AP⊥BC时,此时△ABP为直角三角形;当点P到达点C处时,此时△ABP为等边三角形;当P为CD中点时,△ABP为直角三角形;当点P与点D重合时,此时△ABP为等腰三角形.
4. [2020山东泰安期末]如图,菱形纸片ABCD中,∠A=60°,P为AB的中点,折叠菱形纸片ABCD,使点C落在DP所在直线的C'处,折痕为DE,则∠DEC=　　　　°. 
4.75　如图,连接BD,∵四边形ABCD是菱形,∠A=60°,∴AB=AD,∠ADC=120°,∠C=60°,△ABD是等边三角形.∵P为AB的中点,∴DP平分∠ADB,∴∠ADP=30°,∴∠PDC=∠ADC-∠ADP=90°.由折叠的性质可知∠CDE=∠PDE,∴∠CDE=45°.在△DEC中,∠DEC=180°-∠C-∠CDE=75°.
5. [2021广西大学附属中学期末]如图,菱形ABCD中,∠D=60°,点E,F分别在边BC,CD上,且BE=CF.若EF=2,则△AEF的面积为　　　　. 
6. 如图,菱形ABCD的边长为2,∠DAB=60°,点E为BC边的中点,点P为对角线AC上一动点,则PB+PE的最小值为　　　　. 
7. 原创题 如图,在菱形ABCD中,∠ABC=120°,AB=2,点E是BC的中点,点P是对角线AC上的动点,连接DE,DP,PE.若△DPE是以PE为底的等腰三角形,则AP的长为　　　　. 
8. [2021陕西西安二模]如图,在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.求证:△ABF≌△DAE.
素养提升9. 原创题 在菱形ABCD中,∠BCD=α,点P是对角线BD上一动点(不与点B重合),连接AP,CP,将线段CP绕点C顺时针旋转α得到CQ,连接DQ.(1)如图1,求证:①△BCP≌△DCQ;②AP=CQ.(2)如图2,连接QP并延长交直线AB于点M,PQ与CD交于点N.求证:PM=QN.
9.解:(1)①∵四边形ABCD是菱形,∴BC=DC.由旋转的性质,得CP=CQ,∠PCQ=α.∵∠BCD=∠PCQ=α,∴∠BCP+∠PCD=∠PCD+∠DCQ,∴∠BCP=∠DCQ,∴△BCP≌△DCQ.②∵四边形ABCD是菱形,∴∠ABP=∠CBP,BA=BC.又∵BP=BP,∴△ABP≌△CBP,∴AP=CP.又∵CP=CQ,∴AP=CQ.