




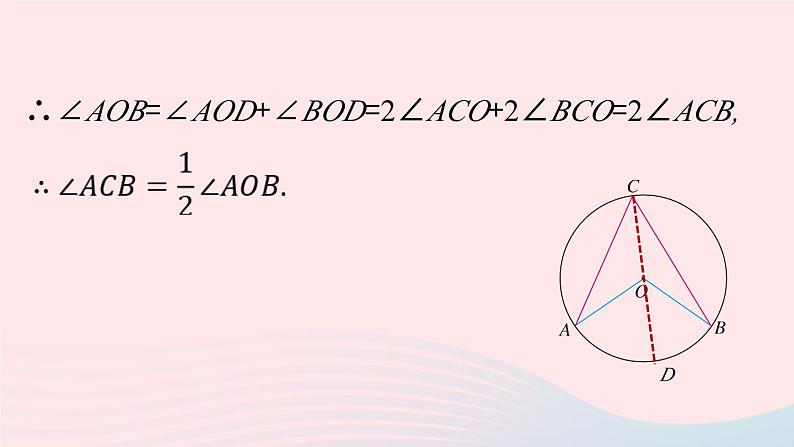
所属成套资源:2023新版新人教版九年级数学上册全一册上课课件(打包46份)
初中数学人教版九年级上册24.1.1 圆教学ppt课件
展开
这是一份初中数学人教版九年级上册24.1.1 圆教学ppt课件,共30页。PPT课件主要包含了知识回顾,在同圆或等圆中,学习目标,课堂导入,知识点1,新知探究,跟踪训练,知识点2,圆周角定理,知识点3等内容,欢迎下载使用。
1.顶点在圆心的角叫圆心角.
2.弧、弦与圆心角的关系定理及推论:
相等的圆心角所对的弧相等,所对的弦也相等;
如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;
如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
2.理解圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题.
1.理解圆周角的概念,会叙述并证明圆周角定理.
3.理解掌握圆周角定理的推论及其证明过程和运用.
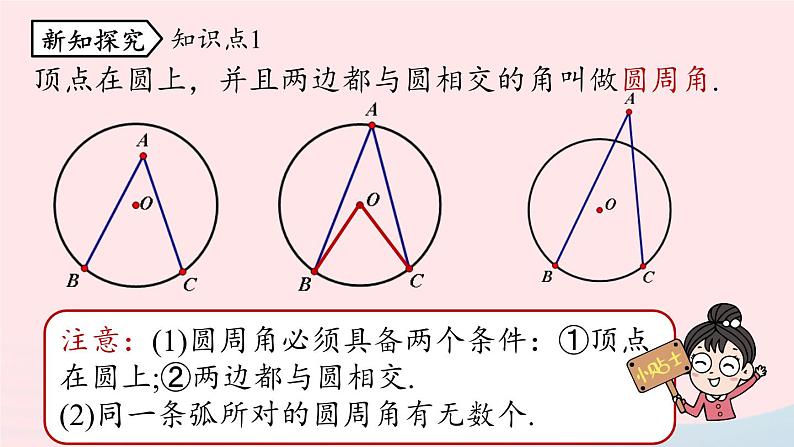
如图,对于∠ACB和∠AOB,我们来研究一下,两个角有何异同点?你知道∠ACB这一类的角的名字吗?
相同:∠ACB和∠AOB两边都与圆相交.
∠ACB顶点在圆上,它叫什么呢?
不同:∠AOB的顶点在圆心,叫做圆心角.
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
注意:(1)圆周角必须具备两个条件:①顶点在圆上;②两边都与圆相交.(2)同一条弧所对的圆周角有无数个.
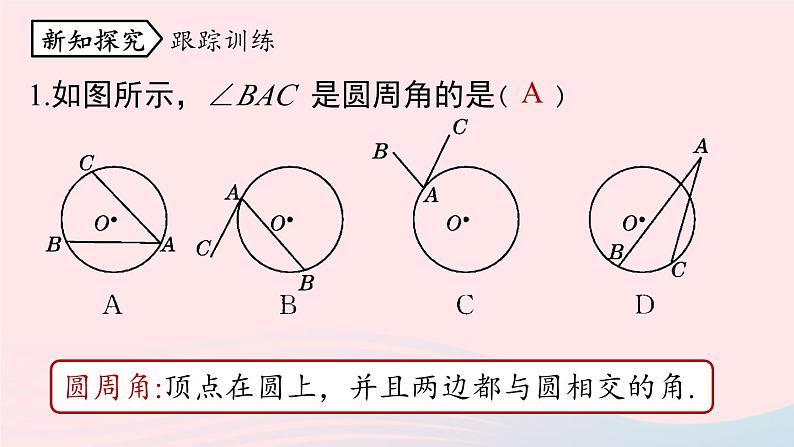
1.如图所示,∠BAC 是圆周角的是( )
圆周角:顶点在圆上,并且两边都与圆相交的角.
如图所示,圆周角∠ACB与圆心角∠AOB所对的弧相等,那么它们之间是否存在什么关系呢?下面我们就来研究这个问题.
①如图,当圆心O在∠ACB内时,连接CO,并延长交圆于点D.
∵△AOC和△BOC是等腰三角形,
∴∠AOD=2∠ACO,∠BOD=2∠BCO,
∴∠AOB=∠AOD+∠BOD=2∠ACO+2∠BCO=2∠ACB,
②如图,当圆心O在∠ACB外时,连接CO,并延长交圆于点D.
∴∠AOB=∠BOD-∠AOD=2∠BCO-2∠ACO=2∠ACB,
∵∠AOB=∠OBC+∠BCO=2∠ACB.
③如图,当圆心O在∠ACB上时.
1.将量角器按如图所示的方式放置在三角形纸板上,使顶点C在半圆上,点A,B的读数分别为100°,150°,则∠ACB的度数为_____°.
一条弧所对的圆周角等于它所对的圆心角的一半.
2.如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为________.
解析:因为∠A=50°,
所以∠BOC=2∠A=100°.
因为∠B=30°, ∠BOC=∠B+∠BDC,
所以∠BDC = ∠BOC - ∠B =70°.
所以∠ADC = 180°- ∠BDC =110°.
探究1:如图,OB,OC都是⊙O的半径,点A,D 是圆上任意两点,连接AB,AC,BD,CD.那么∠BAC与∠BDC相等吗?请说明理由.
所以∠BAC=∠BDC.
所以∠COD=∠EOF,
同弧或等弧所对的圆周角相等.
探究2:如图,线段AB是☉O的直径,点C是 ☉O上的任意一点(除点A、B外),那么,∠ACB就是直径AB所对的圆周角,想一想,∠ACB会是怎样的角?
解:∵OA=OB=OC,∴△AOC,△BOC都是等腰三角形.
∴ ∠OAC=∠OCA,∠OBC=∠OCB.
又∵ ∠OAC+∠OBC+∠ACB=180°,
∴ ∠ACB=∠OCA+∠OCB=180°÷2=90°.
半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
例 如图,⊙O 的直径 AB 为 10 cm,弦 AC为 6 cm,∠ACB 的平分线交⊙O于点D,求BC,AD,BD的长.
在Rt△ABD中,AD2+BD2=AB2,
∵CD平分∠ACB,∴∠ACD=∠BCD.
∵AB 是直径,∴ ∠ACB= ∠ADB= 90°.
∴ ∠AOD=∠BOD,∴AD=BD.
1.(南充中考)如图,BC是⊙O的直径,A是⊙O上的一点,∠OAC=32°,则∠B的度数是( )
A.58°B.60°C.64°D.68°
解析:∵OA=OC,
∴∠C=∠OAC=32°.
∴∠B=90°- 32°=58°.
本题还可用“直径所对的圆周角是直角”求解,可见《教材帮》RJ九上24.1节教材帮·新知课
2.如图,△ABD的三个顶点在⊙O上,AB是直径,点C在⊙O上,且∠ABD=52°,则∠BCD等于( )A.32° B.38° C.52° D.66°
直径所对的圆周角是直角.
1.判断下列图形中的角是不是圆周角,并说明理由.
A.45°B.60°C.75°D.85°
∴∠AOB=2∠BDC=80°,
∴∠AMB≤∠AOB=80°,
则不符合条件的只有85°.
3.(青岛中考)如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( )
A.100°B.110°C.115°D.120°
∴∠ACD= ∠AED=20°,
∴∠BCD=∠ACB+∠ACD=110°.
顶点在圆上,并且两边都与圆相交(二者必须同时具备).
半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
1.如图,⊙O的半径OD⊥AB于点C,连接AO并延长,交⊙O于点E,连接EC.若AB=8,CD=2,则CE的长为( )
解:连接BE,设⊙O的半径为r,则OA=OD=r,OC=r-2,
在Rt△ACO中,由勾股定理,得r2=42+(r-2)2,
解得r=5,∴AE=2r=10,
∵AE为⊙O的直径,∴∠ABE=90°,
由勾股定理,得BE=6,
相关课件
这是一份初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.4 圆周角作业ppt课件,共22页。
这是一份数学九年级上册24.1.1 圆作业课件ppt,共21页。PPT课件主要包含了知识点1圆心角等内容,欢迎下载使用。
这是一份数学九年级上册24.1.1 圆作业ppt课件,共11页。PPT课件主要包含了知识点1圆的定义等内容,欢迎下载使用。










