2023九年级数学上册第二十四章圆24.3正多边形和圆课时1上课课件新版新人教版

这是一份2023九年级数学上册第二十四章圆24.3正多边形和圆课时1上课课件新版新人教版，共31页。

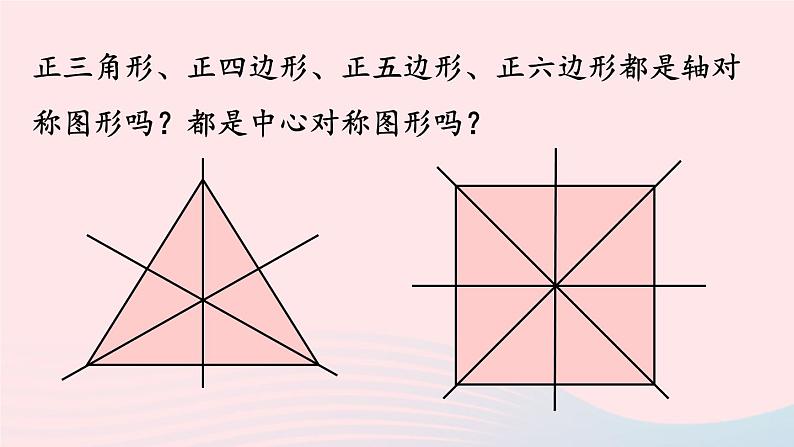
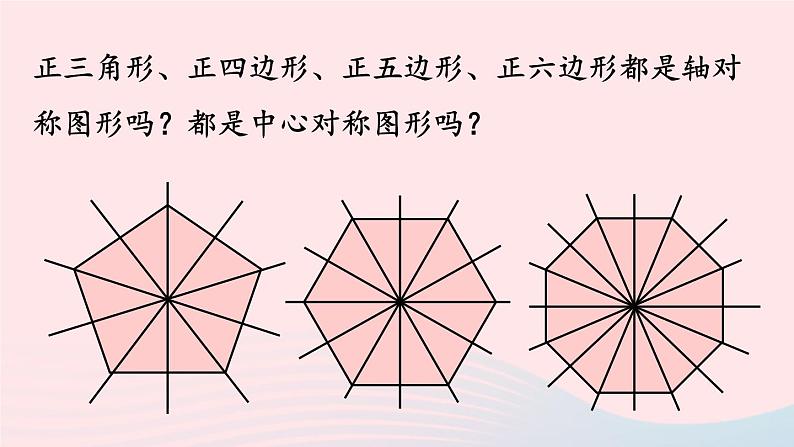
第1课时24.3 正多边形和圆九年级上册 RJ初中数学圆内接四边形的性质：1.对角互补；2.四个内角的和是360°；3.任一外角与其相邻的内角的对角相等(即外角等于内对角)．知识回顾1. 了解正多边形和圆的有关概念.2. 理解并掌握正多边形半径、中心角、边心距、边长之间的关系. 3.会应用正多边形和圆的有关知识解决实际问题.学习目标下面这些美丽的图案，都是在日常生活中我们经常能看到的.你能从这些图案中找出类似的图形吗?课堂导入什么叫做正多边形？各边相等、各角也相等的多边形叫做正多边形.矩形是正多边形吗？为什么？菱形是正多边形吗？为什么？不是，因为矩形不符合各边相等；不是，因为菱形不符合各角相等.知识点1新知探究正三角形、正四边形、正五边形、正六边形都是轴对称图形吗？都是中心对称图形吗？正三角形、正四边形、正五边形、正六边形都是轴对称图形吗？都是中心对称图形吗？正多边形的对称性所有的正多边形都是轴对称图形，一个正n边形共有n条对称轴，每条对称轴都通过正n边形的中心.n为偶数时，它还是中心对称图形，它的中心就是对称中心.OABCD以正四边形为例，根据对称轴的性质，你能得出什么结论？EFGHEF是边AB，CD的垂直平分线，∴OA=OB，OD=OC.GH是边AD，BC的垂直平分线，∴OA=OD，OB=OC.∴OA=OB=OC=OD.∴正方形ABCD有一个以点O为圆心的外接圆.OABCDEFGHAC平分∠DAB及∠DCB，BD平分∠ABC及∠ADC，∴OE=OH=OF=OG.∴正方形ABCD还有一个以点O为圆心的内切圆.以正四边形为例，根据对称轴的性质，你能得出什么结论？所有的正多边形是不是都有一个外接圆和一个内切圆？任何正多边形都有一个外接圆和一个内切圆,并且这两个圆是同心圆.任意三角形都有外接圆和内切圆.任意多边形不一定有外接圆和内切圆.更多讲解见《教材帮》数学RJ九上24.3节教材深挖中心角半径R边心距rO与正多边形有关的概念1.如图所示，△AOB是正三角形，以点O为圆心，OA为半径作☉O，直径FC//AB，AO,BO的延长线分别交☉O于点D,E.求证：六边形ABCDEF为圆内接正六边形.解： ∵ △AOB是正三角形，∴ ∠AOB=∠OAB=∠OBA =60°,OB=OA,∴点B在☉O上.∵FC//AB,∴∠FOA=∠OAB=60°,∠COB=∠OBA= 60°,∴∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠AOF，跟踪训练新知探究1.如图所示，△AOB是正三角形，以点O为圆心，OA为半径作☉O，直径FC//AB，AO,BO的延长线分别交☉O于点D,E.求证：六边形ABCDEF为圆内接正六边形.∴AB＝BC＝CD＝DE＝EF＝AF，∴∴六边形ABCDEF是正六边形．2.如果一个四边形的外接圆与内切圆是同心圆，那么这个四边形一定是(　　)A．矩形 B．菱形 C．正方形 D．不能确定C解: 只有正多边形的外接圆与内切圆才是同心圆，故这个四边形是正方形．故选C.例 有一个亭子，它的地基是半径为4 m的正六边形，求地基的周长和面积 (结果保留小数点后一位).知识点2新知探究 作OP⊥BC垂足为P. 利用勾股定理，可得边心距r=亭子地基的面积S=正n边形的中心角怎么计算？正n边形的边长a，半径R，边心距r之间有什么关系？边长为a，边心距为r的正n边形的面积如何计算？其中l为正n边形的周长.正多边形的有关结论 2.若已知正n边形的边长、周长、边心距、面积中的任意一项，则可求出其他各项.1.正六边形的边长等于其外接圆的半径；正三角形的边长等于其外接圆半径的 倍；正方形的边长等图其外接圆半径的 倍.3.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形.4.正多边形的中心角等于外角，中心角和内角互补.2.作边心距，构造直角三角形.1.连半径，得中心角.·圆内接正多边形的辅助线正多边形的有关计算：1.如果一个正多边形的中心角为72°，那么这个正多边形的边数是(　　)A．4 B．5 C．6 D．7跟踪训练新知探究 B解: 设这个正多边形为正n边形，由题意可知72n＝360，解得n＝5.故选B.·B2.如图,正六边形ABCDEF内接于⊙O，正六边形的周长是12，则⊙O的半径是( 　)A. B．2 C．2 D．2解: 如图，连接OB，OC.∵多边形ABCDEF是正六边形，∴∠BOC＝60°. ∵OB＝OC，∴△OBC是等边三角形，∴OB＝BC.∵正六边形的周长是12，∴BC＝2.∴⊙O的半径是2.故选B.C3.如图所示，正六边形ABCDEF内接于⊙O，则∠ADB的度数是(　　)A．60° B．45° C．30° D．22.5°1.下列圆的内接正多边形中，一条边所对的圆心角最大的图形是( )AA.正三角形 B.正方形 C.正五边形 D.正六边形解:∵正三角形一条边所对的圆心角360°÷3=120°，正方形一条边所对的圆心角是360°÷4=90°，正五边形一条边所对的圆心角是360°÷5=72°，正六边形一条边所对的圆心角是360°÷6=60°，∴一条边所对的圆心角最大的图形是正三角形.故选A.随堂练习2.已知圆的半径是2 ，则该圆的内接正六边形的面积是（ ）A. B. C. D.解:如图，连接正六边形的中心与各个顶点，得到六个等边三角形，∵等边三角形的边长是2 ，∴高是3，∴等边三角形的面积是 ，∴正六边形的面积是 .C·48°3.如图，正五边形ABCDE和正三角形AMN都是⊙O的内接多边形，则∠BOM＝ .解: 如图，连接OA.∵五边形ABCDE是正五边形，∴∠AOB＝ ＝72°.∵△AMN是正三角形，∴∠AOM＝ ＝120°，∴∠BOM＝∠AOM－∠AOB＝48°.更多同类例题见《教材帮》数学RJ九上24.3节作业帮正多边形和圆与正多边形有关的概念正多边形的有关计算添加辅助线的方法：连半径，作边心距中心、半径、边心距、中心角正多边形的性质课堂小结轴对称中心对称1. 以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是( )A  对接中考2.一个上、下底面为全等正六边形的礼盒，高为10 cm，上、下底面正六边形的边长为12 cm，如果用彩色胶带按如图(1)所示的方式包扎礼盒，所需胶带的长度至少为 cm.图(1)图(2) 图(1)图(2) 在Rt∆OBC中，由勾股定理,得OC= cm，∴上、下底面每段胶带的长至少为12 cm，∴所需胶带的长度至少为6×12 +6×10=(72 +60)(cm).2.一个上、下底面为全等正六边形的礼盒，高为10 cm，上、下底面正六边形的边长为12 cm，如果用彩色胶带按如图(1)所示的方式包扎礼盒，所需胶带的长度至少为 cm.题图中只画出了礼盒的部分面，但是在包扎礼盒时，上底面和下底面都是需要彩色胶带的，六个侧面也需要彩色胶带.