初中数学人教版八年级上册第十二章 全等三角形12.2 三角形全等的判定课文配套ppt课件

这是一份初中数学人教版八年级上册第十二章 全等三角形12.2 三角形全等的判定课文配套ppt课件，文件包含1223全等三角形的判定ASAAAS教学课件pptx、人教数学八上122三角形全等的判定第3课时学案+练习docx、第十二章122三角形全等的判定第3课时教学详案docx等3份课件配套教学资源，其中PPT共21页， 欢迎下载使用。
第十二章 全等三角形12.2 三角形全等的判定12.2.3 三角形全等的判定——ASA,AAS
人教版数学八年级上册
3
1
2
通过画、量、观察、比较和猜想等过程，探索、归纳、证明两个三角形全等的条件——ASA,AAS. 掌握用ASA,AAS证明两个三角形全等的方法（重点、难点）．能根据所给条件灵活地选择三角形全等的判定方法，并能综合运用全等三角形的性质证明线段和角相等．
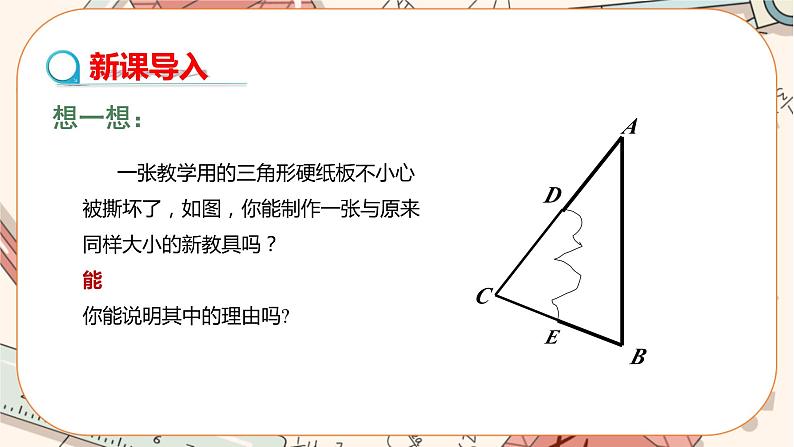
想一想：
一张教学用的三角形硬纸板不小心被撕坏了，如图，你能制作一张与原来同样大小的新教具吗？ 能你能说明其中的理由吗?
C
B
E
A
D
想一想：
探究三角形全等的条件：有三个条件对应相等时
三个角对应相等；三条边对应相等；两条边和一个角对应相等；两个角和一条边对应相等
不能
SSS
?
SAS
探究：
两个角和一条边对应相等时，两三角形是否全等？
思考：已知一个三角形的两个角和一条边，那么这两个角与这条边的位置上有几种可能性呢？
“两角及其夹边”
“两角和其中一角的对边”
它们分别对应相等能判定两个三角形全等吗？
A
B
C
A
B
C
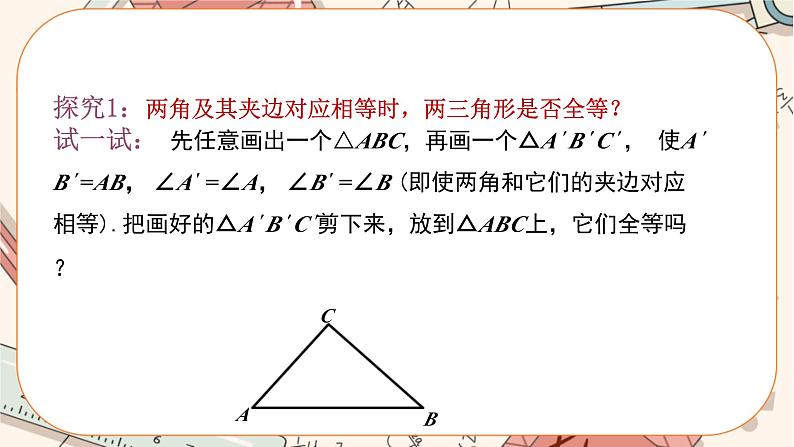
探究1：两角及其夹边对应相等时，两三角形是否全等？
试一试： 先任意画出一个△ABC，再画一个△A ′ B ′ C ′ ， 使A ′ B ′ =AB， ∠A ′ =∠A， ∠B ′ =∠B (即使两角和它们的夹边对应相等).把画好的△A ′ B ′ C ′剪下来，放到△ABC上，它们全等吗？
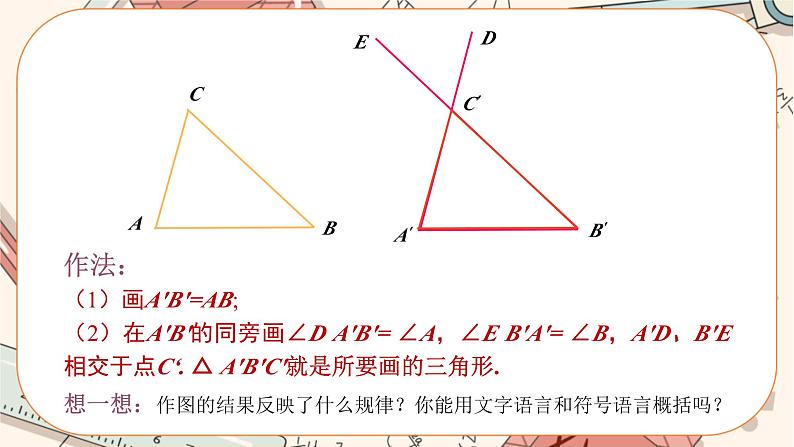
作法：（1）画A'B'=AB;（2）在A'B'的同旁画∠D A'B'= ∠A，∠E B'A'= ∠B，A'D、B'E相交于点C‘. △ A'B'C'就是所要画的三角形.
想一想：作图的结果反映了什么规律？你能用文字语言和符号语言概括吗？
A′
B′
C′
E
D
文字语言：两角和他们的夹边分别相等的两个三角形全等. （简写成“角边角”或“ASA”）
在△ABC和△ DEF中，
∴ △ABC ≌△ DEF（SAS）.
几何语言：
三角形全等的基本事实：角边角（ASA）
∠A=∠D ， AB=DE，∠B=∠E ，


例1
证明：
已知：点D在AB上，点E 在AC上，BE 和 CD 相交于 点O，AB=AC，∠B=∠C. 求证：BD=CE .

例2
证明：
如图：已知AB∥DE，AC∥DF，BE=CF.求证：△ABC≌△DEF.
∵ BE=CF,(已知)
∴BC=EF.(等式性质)
∠B=∠E,
在△ABC和△DEF中,
BC=EF,
∠C=∠F,
∴△ABC≌△DEF.（ASA）
∵ AB∥DE, AC∥DF, (已知)
∴ ∠B=∠DEF , ∠ACB=∠F.
证明：
例3
如图，∠1=∠2，∠3=∠4. 求证：AC=AD.
探究2：两角和其中一角的对边对应相等时，两三角形是否全等？
想一想：在△ABC和△DEF中， ∠A=∠D， ∠B=∠E ，BC=EF，△ABC与△DEF全等吗？能利用角边角条件证明你的结论吗？
由三角形内角和定理得∠C=∠F.
发现： △ABC与△DEF全等
可利用ASA证明全等
文字语言：两角分别相等且其中一组等角的对边相等的两个三角形全等. （简写成“角角边”或“AAS”）
在△ABC和△ DEF中，
∴ △ABC ≌△ DEF（AAS）.
几何语言：
三角形全等的推论：角角边（AAS）
∠A=∠D ， ∠B=∠E ，BC=EF ,
例4
已知：如图， AB⊥BC，AD⊥DC，∠1=∠2. 求证：AB=AD.
∵ AB⊥BC，AD⊥DC，
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中，
∴ △ABC≌△ADC（AAS)，
∴AB=AD.
证明：
1.已知：如图，AB=A′ C ，∠A=∠A′，∠B=∠C. 求证：△ABE≌ △ A′ CD .
∠A=∠A’ 已知AB=A’C 已知∠B=∠C 已知
ABE A’CD ASA
△ABE △A’CD
2. 在△ABC与△A′B′C′中，已知∠A＝44°，∠B＝67°，∠C′＝69° ，∠A′＝44°，且AC＝A′C′，那么这两个三角形（　 ）A．一定不全等　 B．一定全等　 　C．不一定全等　　 D．以上都不对
B
A
B
C
D
E
F
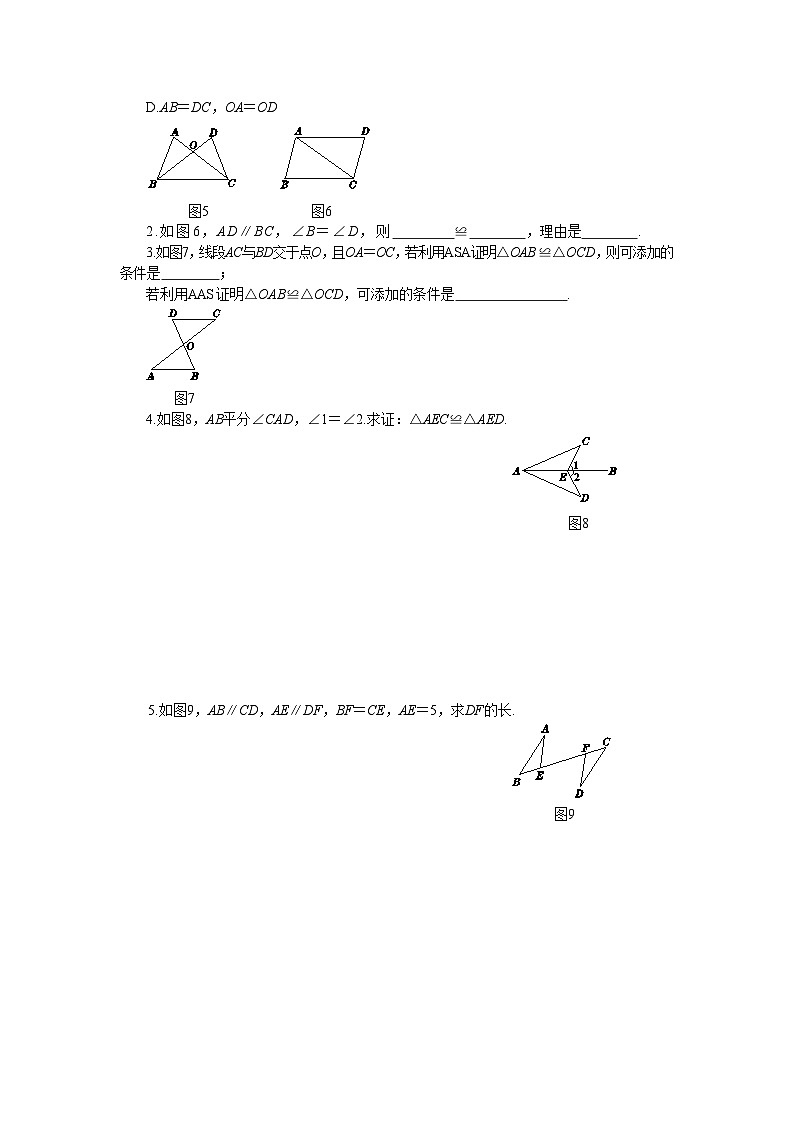
3.如图∠ACB=∠DFE，BC=EF，那么应补充一个条件 ，才能使△ABC≌△DEF （写出一个即可）.
∠B=∠E
或∠A=∠D
或 AC=DF
（ASA）
（AAS）
（SAS）
AB=DE可以吗？
×
AB∥DE
4.
5、如图，AB∥CD，AD∥BC，那么AB=CD吗？为什么？AD与BC呢？
2. 三角形全等的推论：两角分别相等且其中一组等角的对边相等的两个三角形全等.（角角边或AAS）
1. 三角形全等的条件：两角及其夹边对应相等的两个三角形全等. (角边角或ASA)
3.利用全等三角形证明线段或角相等，其思路如下： ⑴观察要证的线段和角在哪两个可能全等三角形之中; ⑵分析要证全等的这两个三角形，已知什么条件，还缺什么条件.
谢谢观看