人教版八年级上册12.2 三角形全等的判定集体备课ppt课件

这是一份人教版八年级上册12.2 三角形全等的判定集体备课ppt课件，文件包含1224全等三角形的判定HL教学课件pptx、人教数学八上122三角形全等的判定第4课时学案+练习docx等2份课件配套教学资源，其中PPT共24页， 欢迎下载使用。

第十二章 全等三角形12.2 三角形全等的判定 12.2.4 直角三角形全等的判定——HL
人教版数学八年级上册
1
2
通过画、量、观察、比较和猜想等过程，探索、归纳、证明两个直角三角形全等的条件——HL. 掌握用HL证明两个三角形全等的方法．
想一想：
对于两个直角三角形，除了直角相等的条件，还要满足几个条件，这两个直角三角形就全等了？ 前面学过的四种判定三角形全等的方法,对直角三角形是否适用？ SSS,SAS,ASA,AAS
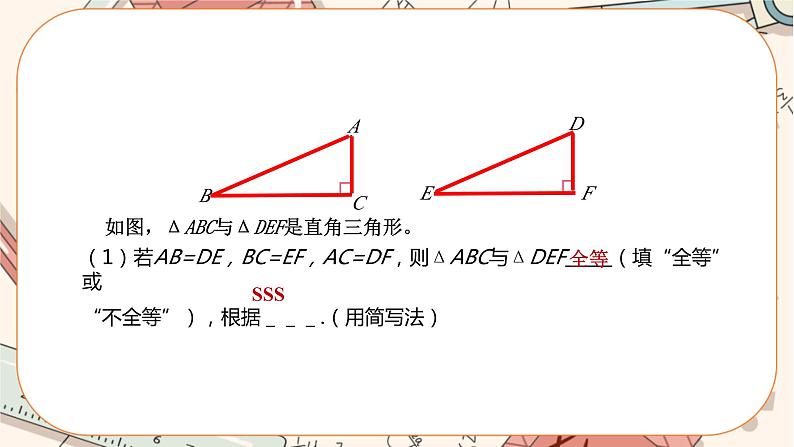
如图，ΔABC与ΔDEF是直角三角形。
C
（1）若AB=DE，BC=EF，AC=DF，则ΔABC与ΔDEF （填“全等”或“不全等”），根据＿＿＿.（用简写法）
全等
SSS
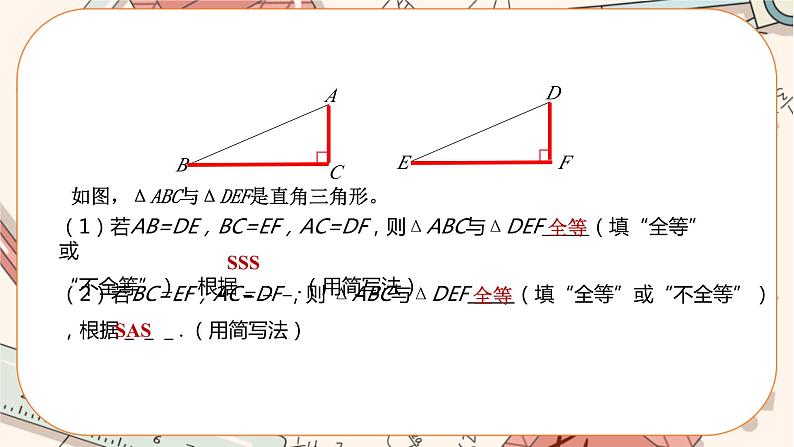
如图，ΔABC与ΔDEF是直角三角形。
C
（1）若AB=DE，BC=EF，AC=DF，则ΔABC与ΔDEF （填“全等”或“不全等”），根据＿＿＿.（用简写法）
（2）若BC=EF，AC=DF ，则 ΔABC与ΔDEF （填“全等”或“不全等”），根据＿＿＿.（用简写法）
全等
全等
SSS
SAS
（3）若∠A=∠D， AC=DF ，则ΔABC与ΔDEF （填“全等”或“不全等”）,根据 .（用简写法）
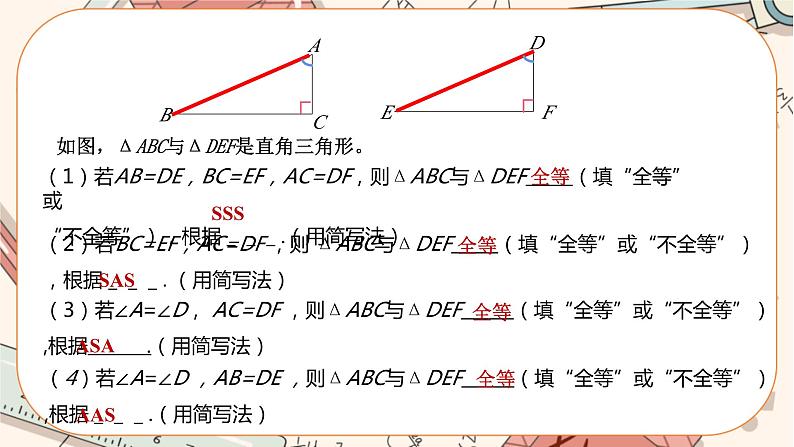
如图，ΔABC与ΔDEF是直角三角形。
C
全等
ASA
（1）若AB=DE，BC=EF，AC=DF，则ΔABC与ΔDEF （填“全等”或“不全等”），根据＿＿＿.（用简写法）
（2）若BC=EF，AC=DF ，则 ΔABC与ΔDEF （填“全等”或“不全等”），根据＿＿＿.（用简写法）
全等
全等
SSS
SAS
（3）若∠A=∠D， AC=DF ，则ΔABC与ΔDEF （填“全等”或“不全等”）,根据 .（用简写法）
如图，ΔABC与ΔDEF是直角三角形。
C
全等
ASA
（4）若∠A=∠D ，AB=DE ，则ΔABC与ΔDEF （填“全等”或“不全等”）,根据＿＿＿.（用简写法）
全等
（1）若AB=DE，BC=EF，AC=DF，则ΔABC与ΔDEF （填“全等”或“不全等”），根据＿＿＿.（用简写法）
（2）若BC=EF，AC=DF ，则 ΔABC与ΔDEF （填“全等”或“不全等”），根据＿＿＿.（用简写法）
全等
全等
SSS
SAS
AAS
C
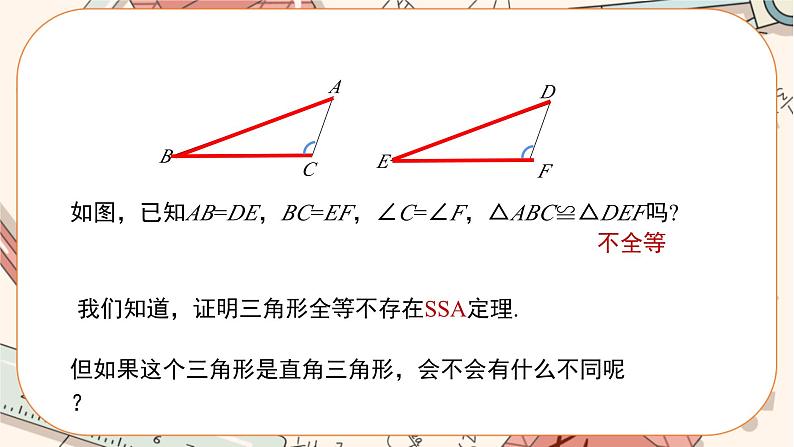
如图，已知AB=DE，BC=EF，∠C=∠F，△ABC≌△DEF吗? 不全等
我们知道，证明三角形全等不存在SSA定理.
F
但如果这个三角形是直角三角形，会不会有什么不同呢？
探究：
直角三角形中，如果满足斜边和一条直角边分别相等，那么这两个直角三角形全等吗？
C
试一试： 任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A ′B ′C ′，使∠C′=90 °,B′C′=BC,A ′B ′=AB,把画好的Rt△A′B′ C′ 剪下来，放到Rt△ABC上，它们能重合吗？
想一想：作图的结果反映了什么规律？你能用文字语言和符号语言概括吗？
步骤：
⑴ 作∠MC＇N=90°;
⑵ 在射线C＇M上截取线段 C＇B＇=CB;
⑶ 以B＇为圆心, AB为半径画弧，交射线C＇N 于点A＇;
⑷连接A＇B＇.
C＇
文字语言：斜边和一条直角边分别相等的两个直角三角形全等（简写 成“斜边、直角边”或“HL”）.
在Rt△ABC和Rt △ DEF中，
∴ Rt △ABC ≌ Rt △ DEF（HL）.
几何语言：
直角三角形全等的判定方法：斜边、直角边（HL）
AB=DE，BC=EF (或AC=DF )，
C
“SSA”可以判定两个直角三角形全等，但是“SS”指的是斜边和一直角边，而“A”指的是直角.


例1
证明：
如图，AB =CD, BF⊥AC,DE⊥AC,AE =CF.求证：BF =DE.
在Rt△ABF 和Rt△CDE 中,∵ AE=CF,∴AF=CE.又∵ AB=CD,∴ Rt△ABF ≌Rt△CDE(HL),∴ BF=DE.


例2
证明：
如图，AC⊥BC， BD⊥AD， AC﹦BD.求证：BC﹦AD.
∵ AC⊥BC， BD⊥AD， ∴∠C与∠D都是直角.
在 Rt△ABC 和Rt△BAD 中，
∴ Rt△ABC≌Rt△BAD (HL).∴ BC﹦AD.
例3
证明：
如图，已知AD、AF分别是两个钝角△ABC和△ABE的高，如果AD＝AF，AC＝AE. 求证：BC＝BE.
∵AD、AF分别是两个钝角△ABC和△ABE的高，且AD＝AF，AC＝AE，∴Rt△ADC≌Rt△AFE(HL),∴CD＝EF.∵AD＝AF，AB＝AB，∴Rt△ABD≌Rt△ABF(HL),∴BD＝BF,∴BD－CD＝BF－EF,即BC＝BE.
1.

如图， ∠ACB =∠ADB=90，要证明△ABC≌ △BAD，还需一个什么条件？把这些条件都写出来，并在相应的括号内填写出判定它们全等的理由. （1） （ ） （2） （ ） （3） （ ） （4） （ ）
AD=BC
∠ DAB= ∠ CBA
BD=AC
∠ DBA= ∠ CAB
HL
HL
AAS
AAS
2.
已知：如图， △ABC中，AB=AC，AD是高.求证:BD=CD ;∠BAD=∠CAD.
A
B
C
D
等腰三角形三线合一
3. 已知：如图，在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF.求证：△ABC≌△DEF.
A
B
C
P
D
E
F
Q
∠BAC=∠EDF, AB=DE,∠B=∠E
分析：
Rt△ABP≌Rt△DEQ
AB=DE,AP=DQ
△ABC≌△DEF
证明：∵AP、DQ是△ABC和△DEF的高, ∴∠APB=∠DQE=90°. 在Rt△ABP和Rt△DEQ中,
AB=DE,
AP=DQ,
∴Rt△ABP≌Rt△DEQ ,(HL)∴ ∠B=∠E. 在△ABC和△DEF中,
∠BAC=∠EDF, AB=DE,∠B=∠E,
∴△ABC≌△DEF. (ASA)
已知：如图，在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF.求证：△ABC≌△DEF.
A
B
C
P
D
E
F
Q
变式1：若把∠BAC＝∠EDF,改为BC＝EF ，△ABC与△DEF全等吗？请说明思路。
已知：如图，在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF.求证：△ABC≌△DEF.
A
B
C
P
D
E
F
Q
变式1：若把∠BAC＝∠EDF,改为BC＝EF ，△ABC与△DEF全等吗？请说明思路。
变式2：若把∠BAC＝∠EDF,改为AC=DF，△ABC与△DEF全等吗？请说明思路。
已知：如图，在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF.求证：△ABC≌△DEF.
A
B
C
P
D
E
F
Q
变式1：若把∠BAC＝∠EDF,改为BC＝EF ，△ABC与△DEF全等吗？请说明思路。
变式2：若把∠BAC＝∠EDF,改为AC=DF，△ABC与△DEF全等吗？请说明思路。
变式3：请你把例题中的∠BAC＝∠EDF改为另一个适当条件，使△ABC与△DEF仍能全等。试证明。
SAS
ASA
AAS
SSS
SAS
ASA
AAS
HL
灵活运用各种方法证明直角三角形全等.
SSS
谢谢观看