湖南省衡阳市衡南县2022-2023学年八年级上学期期末数学试题（含答案）

这是一份湖南省衡阳市衡南县2022-2023学年八年级上学期期末数学试题（含答案），共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022年下学期期末教学质量检测试卷
八年级数学
时量：120分钟 满分：120分
请考生注意：请把答案写在2~6页的答卷上
一、选择题（本大题12小题，每小题3分，共36分）
1．9的算术平方根是（ ）
A．3 B． C． D．
2．下列叙述正确的是（ ）
A． B．5的平方根是 C．是5的一个平方根 D．是分数
3．下列运算正确的是（ ）
A． B． C． D．
4．已知一个等腰三角形的两边长分别是2和4，则该等腰三角形的周长为（ ）
A．8或10 B．8 C．10 D．6或12
5．一个正方形的面积是10，估计它的边长大小在（ ）
A．2和3之间 B．3和4之间 C．4和5之间 D．5和6之间
6．若的三边满足，则是（ ）
A．等腰三角形 B．直角三角形 C．等腰直角三角形 D．等腰三角形或直角三角形
7．如图，是等腰三角形的顶角平分线，，则等于（ ）

A．10 B．5 C．4 D．3
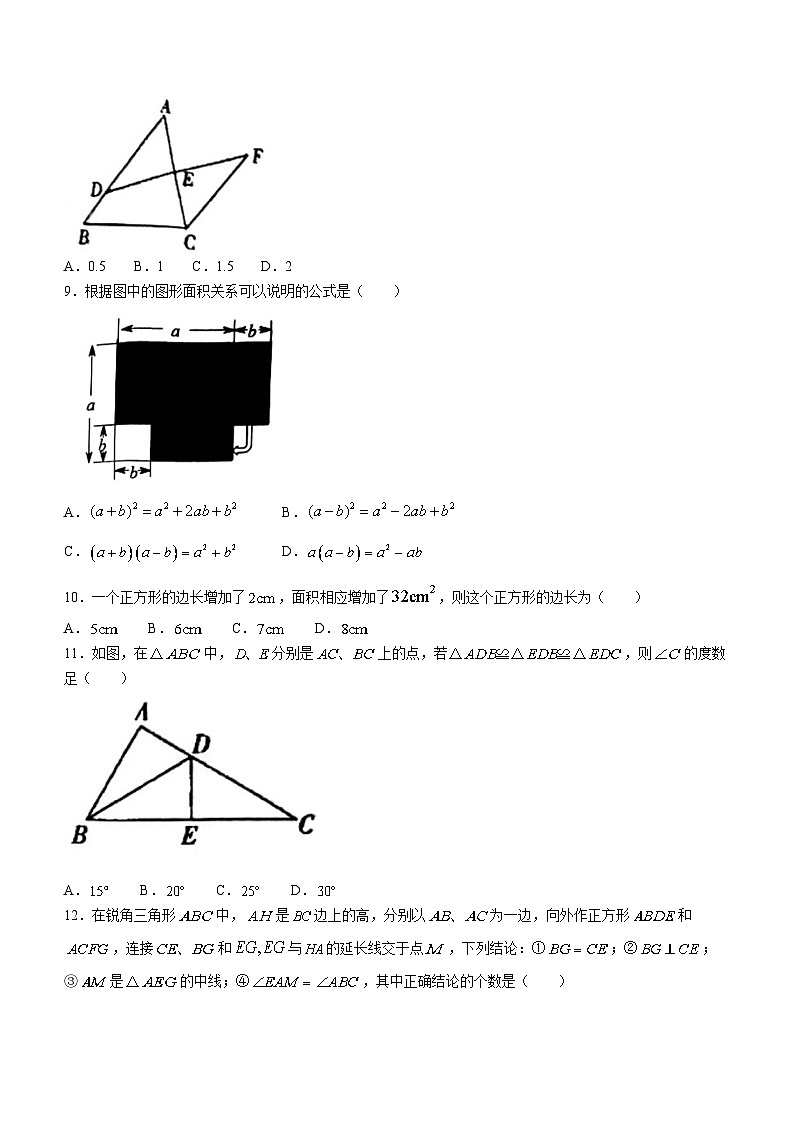
8．如图，是上一点，交于点，若，则的长是（ ）

A．0.5 B．1 C．1.5 D．2
9．根据图中的图形面积关系可以说明的公式是（ ）

A． B．
C． D．
10．一个正方形的边长增加了，面积相应增加了，则这个正方形的边长为（ ）
A． B． C． D．
11．如图，在中，分别是上的点，若，则的度数足（ ）

A． B． C． D．
12．在锐角三角形中，是边上的高，分别以为一边，向外作正方形和，连接和与的延长线交于点，下列结论：①；②；③是的中线；④，其中正确结论的个数是（ ）

A．4个 B．3个 C．2个 D．1个
二、填空题（本大题6小题，每小题3分，共18分）
13．某个数的一个平方根是，则这个数是_______________．
14．若，则_______________．
15．某校对1200名女生的身高进行测量，身高在这一小组的频率为0.25，则该组的人数为_______________名．
16．分解因式：_______________．
17．则图，在中已知的平分线相交于点，过点作，交于点，交点，若，则的周长为_______________．

18．如图，以数轴的单位长度线段为边长作一个正方形，以表示数的点为圆心、正方形对角线长为半径画半圆，交数轴于点和点，则点表示的数是_______________．

三、解答题（本大题8小题，共66分）
19．计算（6分）：
20．（6分）如图，，

求证：．
21．（8分）先化简，再求值：
，其中
22．（8分）进入秋冬季，低温环境下新冠病毒由“物”传“人”风险增加，流感等呼吸道传染病也进入高发期，防疫仍不能掉以轻心．为了更好的防护、我们务必要了解病毒及基本防护知识．为了解市民对“病毒与防护”知识的了解情况，市疾控中心对某小区进行了一次抽样调查，把居民对“病毒及防护”的了解情况分为四个层次：A了解病毒，能基本防护；B不了解病毒，但能基本防护；C了解病毒，但不会基本的防护；D不了解也不会基本的防护，并将调查结果绘制了图1和图2两幅不完整的统计图．
请你根据图中提供的信息解答下列问题：

（1）本次被抽查的居民有多少人？
（2）将图1和图2补充完整；
（3）求出图2中“C”层次所在扇形的圆心角的度数；
（4）估计该小区4000名居民中“能基本防护”（包括A层次和B层次）的大约有多少人．
23．（8分）如图，在和中，，且，点在上．过点作且交于点，连接．

求证：（1）；
（2）．
24．（8分）已知如图，在，为边边上的中线，过点作，垂足为，在直线上截取．

求证：（1）；（2）若，求的长．
25．（10分）阅读材料：数学课上，老师在求代数式的最小值时，利用公式：，对式子作如下变形：，
因为，所以，
当时，，
因此有最小值1，即的最小值为1．
通过阅读，解下列问题：
（1）代数式的最小值为_______________，此时的值为_______________
（2）试比较代数式与的大小，并说明理由．
26．（12分）如图，在中，在上，且，过点作射线（与在同侧），若动点从点出发，沿射线匀速运动，运动速度为，设点运动时间为秒．

（1）经过_______________秒时，是等腰直角三角形?
（2）当于点时，求此时的值；
（3）过点作于点，已知，请问是否存在点使是以为腰的等腰三角形?对存在的情况，请求出的值，对不存在的情况，请说明理由．
衡南县八年级期末考试试卷
数学参考答案
一、选择题
1．A 2．C 3．C 4．C 5．B 6．C 7．B 8．B 9．C 10．C 11．D 12．A
二、填空题
13．25 14．3 15．300 16． 17．16 18．
三、解答题
19．解：原式；
20．证明：如图，，
在与中，
．
21．解：
，
当时，原式；
22．（1）本次被抽查的居民有：（人）．
（2）的人数的人数为：（人），
的人数为：（人），
所占的比例为：，
所占的比例为：；
将图1和图2补充完整如下：

（3），
（4）（人），
23．（1）证明：，
，
在和中

；
（2）证明：，
，

即．
24．（1）证明：，

在和中

；
（2）解：是边的中线，
．
25．（1）3，3（2）大于
26．解：（1）当是等腰直角三角形时，，
，
（2）当时，，
，又，
，
在和中，

，
经过8秒时，．
（3）存在．
理由：根据勾股定理得，的最小值为8，
，当时，
在和中，
，
，
则当是以为腰的等腰三角形时，．