数学5.4 一元一次方程的应用教案

5.4一元一次方程的应用

第   2  课时相遇、工程问题

教学目标

(1)掌握相遇问题、工程问题中的基本等量关系；

(2)学会利用线段图分析相遇问题及工程问题，分清有关数量关系，正确找出作为列方程依据的主要等量关系；

教学重点

掌握相遇问题、工程问题中的基本等量关系；

教学难点

学会利用线段图分析相遇问题及工程问题，分清有关数量关系，正确找出作为列方程依据的主要等量关系；

教学过程

一、导入新课

二、试着做做

问题1：甲、乙两地间的路程为375km.一辆轿车和一辆公共汽车分别从甲、乙两地同时出发沿公路相向而行.轿车的平均速度为90km/h，公共汽车的平均速度为60km/h.它们出发后多少小时在途中相遇？

分析：

（1）线段图     

       甲                                         乙

（2）等量关系：_____________+___________=_____________.

（3）设出发后x小时相遇，则：

（4）列方程__________________

           解得x=_________________

       答：它们出发后______小时相遇.

（5）请解这个方程

三、例题解析

例2  一项工作，小李单独做需要6h完成，小王单独做需要9h完成.如果小李先做2h后，再由两人合做，那么还需几小时才能完成 ？

分析：（1）线段图

（2）等量关系：__________+____________=______________.

（3）设小李和小王合作还需要     小时才能完成全部工作，则

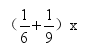
（4）列方程__________________

     解得_________________

     答：小李和小王合作还需要     小时才能完成全部工作

四、当堂检测：

（1）.A、B两地相距450千米，甲、乙两车分别从A、B两地同时出发，相向而行.已知甲车的速度为120千米/时，乙车的速度为80千米/时，t小时后两车相遇，则t=_______.

（2）.加工1 500个零件，甲单独做需要12小时，乙单独做需要15小时，若两人合做x小时可以完工，依题意可列方程为(   )

A.     B. C.   D.

（3）、一项工程，甲队单独完成需要20天，乙队单独完成需要30天，如果先由甲队单独做5天，则剩下部分由甲、乙两队合作完成还需要的天数是（   ）

A.9      B.10     C.12      D.15

（4）.一件工作由一个人做要500小时完成，现在计划由一部分人先做5小时，再增加8人和他们一起做10小时，完成了这项工作，问：先安排多少人工作？

五、课堂小结

通过本节课的学习，你的收获是？

六、板书设计

5.1一元一次方程的应用（2）

（1）一元一次方程的应用

（2）常见的实际问题