华师版·吉林省长春市北京师范大学附属实验学校2022-2023学年八上期末数学试卷

这是一份华师版·吉林省长春市北京师范大学附属实验学校2022-2023学年八上期末数学试卷，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

八年级期末质量检测——数学试卷
一、选择题（每题3分，共24分）
1. 4的平方根是（ ）
A. 2 B. C. D.
2. 下列各数是无理数的是（ ）
A. B. C. D.
3. 下列代数式中，是分式的是（ ）
A. B. C. D.
4. 计算：结果为（ ）
A. B. C. D.
5. 分式有意义，x的取值范围是（ ）
A. B. C. D.
6. 小明在纸上写下一组数字“”这组数字中2出现的频数为（ ）
A. B. C. 3 D. 5
7. 如图，在中，，以顶点A为圆心，适当长为半径画圆弧，分别交于点D、E，再分别以点D、E为圆心，大于长为半径画圆弧，两弧交于点F，作射线交边于点G．若，则面积是（　　）

A. 150 B. 120 C. 80 D. 60
8. 如图，一长方体木块长，宽，高， 一直蚂蚁从木块点A处，沿木块表面爬行到点位置最短路径的长度为（ ）

A B. C. D.
二、填空题（每题3分，共18分）
9. 比较大小：______．
10. 用科学计数法表示________．
11. 命题“对顶角相等”的逆命题是一个__________命题（填“真”或“假”）．
12. 一个直角三角形的两条直角边分别为3和4，则该直角三角形的斜边为______．
13. 已知关于x多项式是完全平方式，则k的值为_______．
14. 等腰中，，点E为底边上一点，以点E为圆心，长为半径画弧，交于点D，测得，，则_____°．

三、解答题（共78分）
15. 分解因式：
（1）
（2）


16 先化简，再求值：，其中．









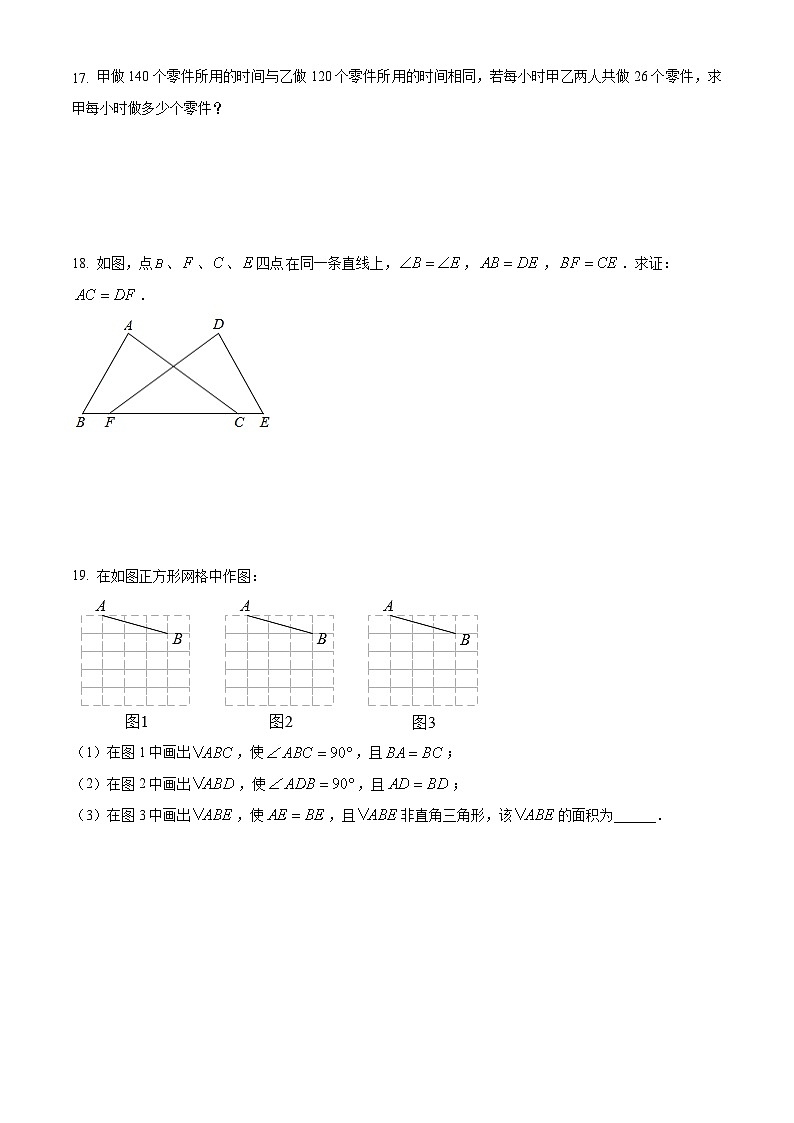
17. 甲做140个零件所用的时间与乙做120个零件所用的时间相同，若每小时甲乙两人共做26个零件，求甲每小时做多少个零件？




18. 如图，点、、、四点同一条直线上，，，．求证：．





19. 在如图正方形网格中作图：

（1）在图1中画出，使，且；
（2）在图2中画出，使，且；
（3）在图3中画出，使，且非直角三角形，该的面积为______．







20. 第24届冬季奥林匹克运动会在中国北京和张家口市联合举行．某校为了解九年级学生对冬季奥林匹克运动会相关知识的掌握情况，从九年级学生中随机抽取部分学生进行测试，并对成绩（百分制）进行整理、描述和分析．部分信息如下：
a．测试成绩等级标准如下：
等级
A
B
C
D
E
分数x的范围





b．九年级学生成绩频数分布直方图和各等级人数的扇形统计图（如图）：

请根据以上信息回答下面问题：
（1）本次调查中“E”等级有______人；
（2）本次共调查了______人，成绩在分的有______人；
（3）求扇形统计图中“D”对应扇形的圆心角的大小为______．




21. 已知，求代数式







22. 如图，在中，，将沿折叠，使点B落在边上点D的位置．

（1）若，求的度数；
（2）若；
①求的长；
②的面积为______．



23. 与均为等腰直角三角形，连接、．
（1）如图1，点E在线段上，则与的数量关系为______，位置关系为_______．

（2）将绕点B顺时针旋转至图2位置时，（1）中的两个结论是否还成立，如果成立，请分别证明；如果不成立，请说明理由．
（3）若在图2中，连接、，且， ，则=______．






24. 如图，在中，，，，点P从点C出发，以每秒3个单位长度的速度沿折线运动.设点P的运动时间为t（）．

（1）_______；
（2）求斜边上的高线长．
（3）①当P在上时，的长为_______，t的取值范围是_____（用含t的代数式表示）
②若点P在的角平分线上，则t的值为______．
（4）在整个运动过程中，直接写出是以为一腰的等腰三角形时t的值．
参考答案
一、1~5：BCCAB 6~8：DDB
二、9. 10. 11.假 12.5 13.9或 14.31
三、15. 【小问1详解】
解：
；
【小问2详解】


．
16.


当时，
原式．
17. 设甲每小时做个机器零件，则乙每小时做个机器零件，
依题意得：，
解得：，
经检验：是原分式方程的解，且符合题意，
答：甲每小时做14个机器零件．
18. 证明：∵BF＝CE，
∴BF+FC＝CE+FC，
即BC＝EF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SAS），
∴AC＝DF．
19. 【小问1详解】
解：如图所示，即为所求，，


∴是直角三角形，，且
【小问2详解】
如图所示，即为所求；，

∴
∴是直角三角形，，且
【小问3详解】
如图所示，即为所求；，面积为

20. 【小问1详解】
解：根据图①可得，“E”等级有5人，
故答案为：5；
【小问2详解】
由（1）得“E”等级有5人，由图②得“E”等级所占比例为10%，
∴总人数为：人，
由图①得：“A”等级有11人，“B”等级有12人，“D”等级有10人，“E”等级有5人，
∴“C”等级有人，
故答案为：50；12；
【小问3详解】
由（2）得“D”等级有10人，
∴圆心角度数为：，
故答案为：
21. ∵，
∴，，，
∴，
∴



22. 【小问1详解】
解：∵沿折叠，使点B落在边上点D的位置，
∴
∵
∴
∴
又∵
∴；
【小问2详解】
①∵沿折叠，使点B落在边上点D的位置，，
∴，
∵，
∴．
∴，
设，则，
∴，即，
解得：，
∴的长为6；
②由①得，
∴，
∴
故答案为：60．
23. 【小问1详解】
解：延长交于点F，如图所示：

∵与均为等腰直角三角形，
∴，，，
∴，
∴，，
∵，
∴，
∴，
∴．
故答案为：相等；垂直．
【小问2详解】
解：（1）中的两个结论成立；理由如下：

∵与均为等腰直角三角形，
∴，，，
∴，
即，
∴，
∴，，
∵，，
∴，
∴，
∴．
小问3详解】
解：连接，，如图所示：

∵，
∴，
∴、、、为直角三角形，
∴，，
，，
∴，
，
∴，
故答案为：18．
24.【小问1详解】
解：在中，，，，
，
故答案为：12；
【小问2详解】
解：如图所示，过点作于点，

，
即，
∴斜边上的高线长为；
【小问3详解】
解：①点P从点C出发，以每秒3个单位长度的速度沿折线运动，，
，
，即
，
②点在的角平分线上时，过点作于，如图所示，

∵平分，，，
∴，
又∵，
∴，
∴，则，
由（2）知，
∴，
∴，
在中，，即，
解方程得，，
∴点在的角平分线上时，．
故答案为：①；；②；
【小问4详解】
解：是以为一腰的等腰三角形时，有两种情况：
当时，如图所示，

则，
；
当时，过点作于点，如图所示，

由（2）知，
，
，，
，
，
；
故是以为一腰的等腰三角形时t的值为或．