华师版·河南省南阳市邓州市2022-2023学年八上期中数学试卷

这是一份华师版·河南省南阳市邓州市2022-2023学年八上期中数学试卷，共13页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。

邓州市2022～2023学年第一学期期中质量评估八年级数学试卷
一、选择题（每小题3分，共30分）请将唯一正确答案的序号涂在答题卡上．
1. 有理数9算术平方根是（ ）
A. B. C. 3 D.
2. 下列各数中，是无理数的是（ ）
A. B. C. D.
3. 老师在黑板上书写了一个正确的算式，随后用手掌遮住了一个单项式，形式如下：=，则处应为（　　　）
A. B. a C. D.
4. 地球的体积约为立方千米，太阳的体积约为立方千米，太阳的体积约是地球体积的倍数是（ ）
A. B. C. D.
5. 下列命题属于真命题的是（　　）
A. 若a=b，则a2=b2 B. 三个角对应相等的两个三角形是全等三角形
C. 无限小数都是无理数 D. 若|x|=|y|，则x=y
6. 下列能用平方差公式计算的是（ ）
A. B. C. D.
7. 如图，把两根钢条的中点连在一起，可以做成一个测量工件内槽宽的工具（卡钳）．在图中，要测量工件内槽宽AB，只要测量A′B′就可以，这是利用什么数学原理呢？（ ）

A. AAS B. SAS C. ASA D. SSS
8. 如图有三种不同的纸片，现选取4张拼成了图甲，你能根据面积关系得到下列等式成立的是（ ）

A. B.
C. D.
9. 如图，在中， ，将沿翻折后，点A落在BC边上的点处．若，则的度数为（ ）

A. B. C. D.
10. 如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（ ）

A. 1个 B. 2个 C. 3个 D. 4个
二、填空题（每小题3分，共15分）
11. 如果一个数的立方根是其本身，则这个数是_______．（写一个即可）
12. 已知，，则的值为_________．
13. 计算：_______．
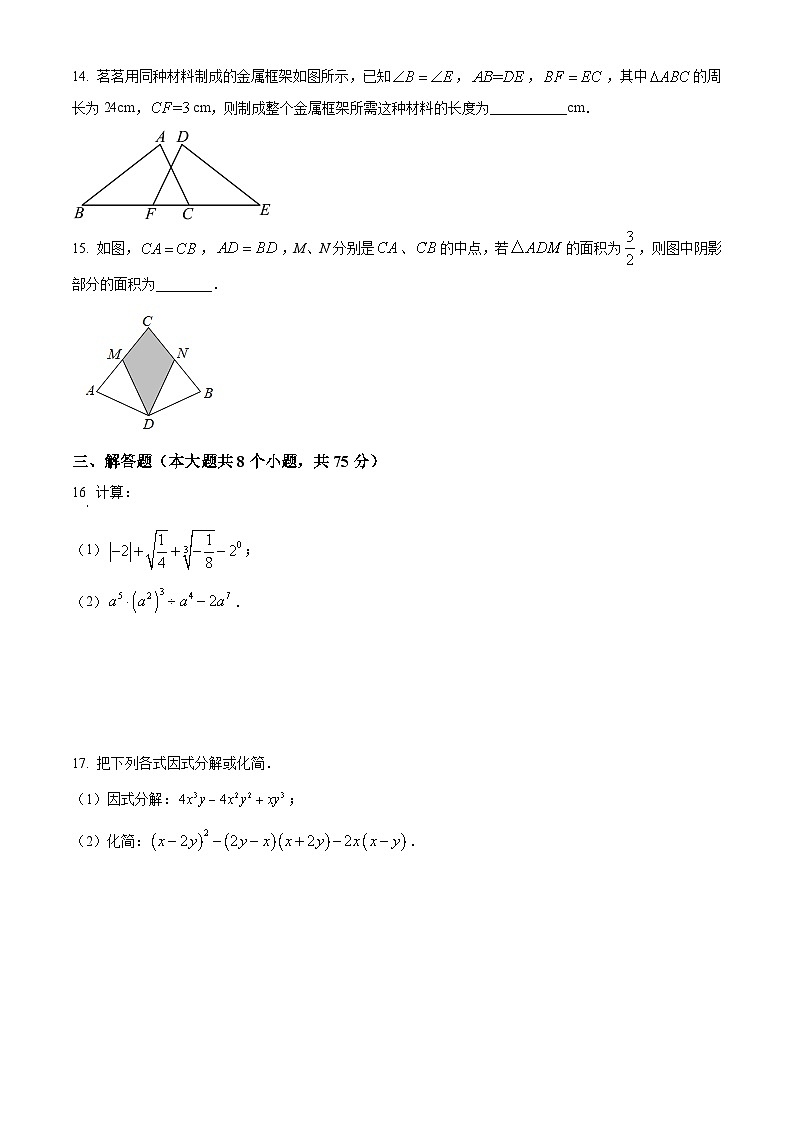
14. 茗茗用同种材料制成的金属框架如图所示，已知，，，其中的周长为24cm，cm，则制成整个金属框架所需这种材料的长度为___________cm．

15. 如图，，，M、N分别是、的中点，若的面积为，则图中阴影部分的面积为________．

三、解答题（本大题共8个小题，共75分）
16 计算：
（1）；
（2）．




17. 把下列各式因式分解或化简．
（1）因式分解：；
（2）化简：．





18. 在运算中，我们如果能总结规律，并加以归纳，得出数学公式，一定会提高解题的速度．在解答下列问题中，请探究其中的规律．
（1）计算后填空：_________；
_________；
_________；
（2）归纳猜想后填空：____________
（3）运用（2）中得到的结论，直接写出计算结果：______．





19. 如图1，油纸伞是中国传统工艺品之一，起源于中国一种纸制或布制年，油纸伞的制作工艺十分巧妙，如图2，伞圈沿着伞柄滑动时，总有伞骨，从而使得伞柄始终平分同一平面内两条伞骨所成的．为了说明这一制作方法的正确性，需要对其进行证明．如下给出了不完整的“已知”和“求证”，请补充完整，并写出“证明”过程
已知：如图2，点，，，在同一平面内，___________，_____________．
求证：_________________．







20. 认真观察图形，解答下列问题：

（1）根据图①中的条件，试用两种不同的方法表示两个阴影图形的面积的和．
方法1：_________________；方法2：_________________﹔
（2）从中你能发现什么结论?请用等式表示出来：__________________；
（3）利用（2）中结论解决下面的问题：如图②，两个正方形的边长分别为m，n，如果，求阴影部分的面积．



21. 如图，，相交于点C， ，点P从点A出发，沿方向以的速度匀速运动，点Q从点D出发，沿方向以的速度匀速运动．P，Q两点同时出发，当点P回到点A时，P，Q两点同时停止运动．设点P的运动时间为．

（1）当时．_____，当时，_______．
（2）求证：．
（3）连接，当线段经过点C时，的长为______．




22. 先阅读理解下面的例题，再按要求解答下列问题：
例题：试说明代数式的值一定是正数．
解：．
∵，
∴．
∴的值一定是正数．
（1）判断代数式的值一定是（ ）
A．0 B．1 C．负数 D．正数
（2）说明代数式值一定是负数．
（3）设正方形面积为，长方形的面积为，正方形的边长为，如果长方形的一边长比正方形的边长少，另一边长为，请你比较与的大小关系，并说明理由．

















23. 已知是经过顶点C的一条直线，，E，F是直线上的两点，且．

（1）观察猜想；如图①．当直线经过的内部，且E，F在射线上时，若，则_____，____ ；（填“>”“<”或“=”）
（2）类比探究：如图②，在（1）的条件下，若，则①中的两个结论是否仍然成立，若成立，请证明；若不成立，请说明理由；
（3）反思提升；如图③，当直线不经过的内部，且时，若，请直接写出BC的取值范围．

参考答案
一、1~5：CBCAA 6~10：CBDCC
二、11.、1、0（写出一个即可给分） 12.-6 13. 14.45
15.3
三、16.
【小问1详解】
解：


【小问2详解】
解：




17. 【小问1详解】
．
【小问2详解】
解：

．
18.【小问1详解】



故答案为：；；．
【小问2详解】

故答案为：，．
【小问3详解】

故答案为：．
19. 已知：，．
求证：（或AD平分）
故答案为：，，（或AD平分）
证明：在和中，∴
∴

20. 【小问1详解】
解：因为两个阴影图形，分别为边长为a，b的正方形，
所以阴影部分的面积为两个正方形的面积和，
所以面积为；
因为两个阴影图形的面积，可以表示为边长为的正方形面积，与两个矩形的面积之差，
所以阴影部分的面积为；
故答案为：方法1：（或）；方法2：（或）
【小问2详解】
根据等式的性质，得到或，
故答案为：或．
【小问3详解】
阴影部分的面积为：

．
21. 【小问1详解】
解：当时．，
当时．，
故答案为：3，2；
【小问2详解】
解：在和中，
，
，
，
；
【小问3详解】
解：由（1）得，
，，
当线段经过点C时，如下所示：

在和中，
，
，
，
，点P从点A出发，沿方向以的速度匀速运动，
时，点P到达点B，时，点P返回点A，
，
当时，，
解得，
的长为；
当时，，
解得，
长为；
综上所述，的长为或，
故答案为：1或2．
22. 【小问1详解】
解：

，
∵，
∴，
∴的值一定是正数
故选：D
【小问2详解】
解：


∵，
∴，
∴的值一定是负数
【小问3详解】
，理由如下：
根据题意得：，，
∴



∵，
∴，
∴．
23.【小问1详解】
因为，，
所以， ，
所以，
所以，

所以，
所以，
所以，
所以填“=”，“=”．
故答案为：=；=．
【小问2详解】
结论仍成立，理由如下：
因为，，
所以，
所以，
所以，

所以，
所以，
所以．
故结论仍成立．
【小问3详解】
如图，因为，，
所以， ，
所以，
所以，
所以，
所以，
所以，

因为，
所以，
所以．
所以．