华师版·河南省南阳市宛城区2022-2023学年八上期中数学试卷

这是一份华师版·河南省南阳市宛城区2022-2023学年八上期中数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022年秋期期中质量评估检测
八年级数学试题卷
一、选择题（每小题3分，共30分）下列各小题均有四个选项，其中只有一个是正确的）
1. 化简的结果是（　　）
A. a B. C. D.
2 式子表示（ ）
A. 的算术平方根 B. 的算术平方根 C. 的平方根 D. 的算术平方根
3. 下列四个数中，不是无理数的是（ ）
A. B. C. D.
4. 若等腰三角形的周长为26cm，一边为6cm，则腰长为（　　　）
A 6cm B. 10cm C. 10cm或6cm D. 以上都不对
5. 计算的结果是（ ）
A. B. C. D.
6. 如图，为了估算河的宽度，我们可以在河的对岸选定一个目标点A，再在河的这一边选定点B和F，使AB⊥BF，并在垂线BF上取两点C、D，使BC＝CD，再作出BF的垂线DE，使点A、C、E在同一条直线上，因此证得△ABC≌△EDC，进而可得AB＝DE，即测得DE的长就是AB的长，则△ABC≌△EDC的理论依据是（ ）

A. SAS B. HL C. ASA D. AAA
7. 在多项式上添加一个单项式，使得到的单项式可以用完全平方公式进行因式分解，则添加的单项式不可以是（ ）
A. B. C. D.
8. 若，则n的值是（ ）
A. 2023 B. 2022 C. 2021 D. 2020
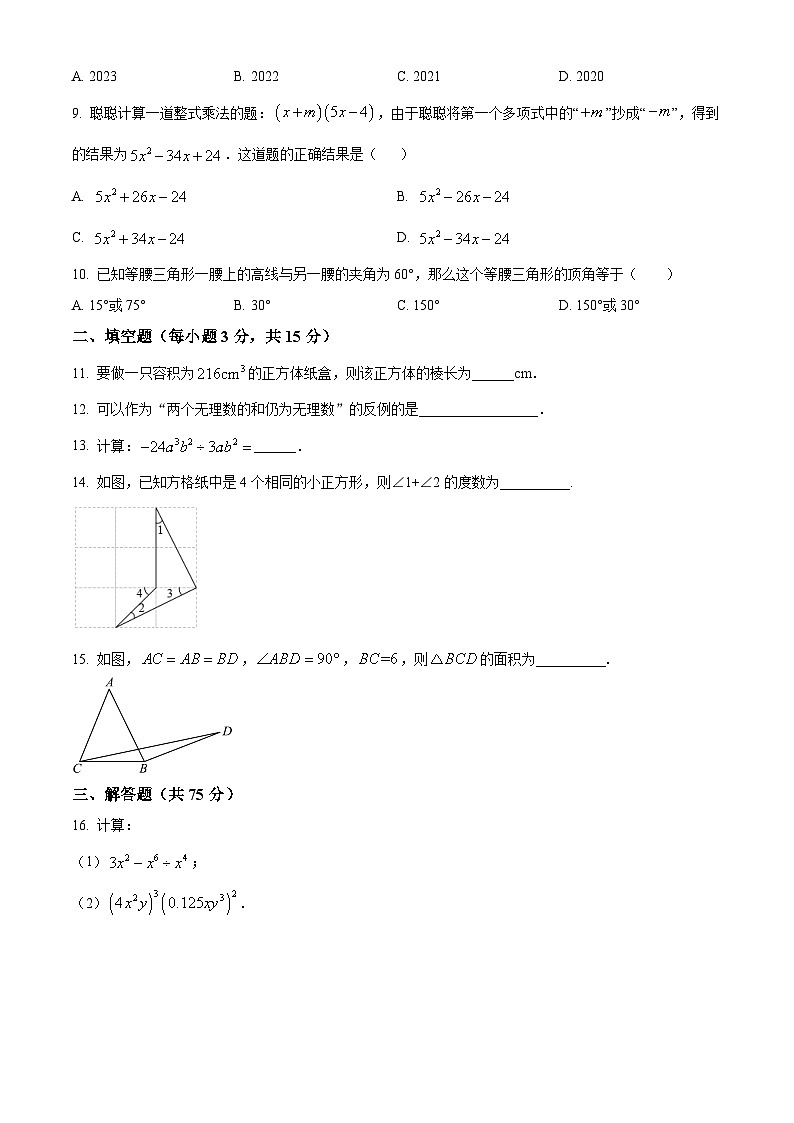
9. 聪聪计算一道整式乘法的题：，由于聪聪将第一个多项式中的“”抄成“”，得到的结果为．这道题的正确结果是（ ）
A. B.
C. D.
10. 已知等腰三角形一腰上的高线与另一腰的夹角为60°，那么这个等腰三角形的顶角等于（　　）
A. 15°或75° B. 30° C. 150° D. 150°或30°
二、填空题（每小题3分，共15分）
11. 要做一只容积为的正方体纸盒，则该正方体的棱长为______cm．
12. 可以作为“两个无理数的和仍为无理数”的反例的是_________________．
13. 计算：______．
14. 如图，已知方格纸中是4个相同的小正方形，则∠1+∠2的度数为__________.

15. 如图，，，，则的面积为__________.

三、解答题（共75分）
16. 计算：
（1）；
（2）．



17. 将幂的运算逆向思维可以得到，，，，在解题过程中，根据算式的结构特征，逆向运用幂的运算法则，常可化繁为简，化难为易，使问题巧妙获解．
（1）已知，，求：
①的值；
②的值；
（2） 已知，求的值．




18. 阅读理解．
∵＜＜，即2＜＜3．
∴1＜﹣1＜2
∴﹣1的整数部分为1，
∴﹣1的小数部分为﹣2．
解决问题：已知a是﹣3的整数部分，b是﹣3的小数部分．
（1）求a，b的值；
（2）求（﹣a）3+（b+4）2的平方根，提示：（）2＝17．










19 已知：如图，、交于点，，请你再添加一个条件（不再添加其他辅助线，不再标注或使用其他字母），使，并给出证明．




20. 在分解因式时，小彬和小颖对同一道题产生了分歧，下面是他们解答过程，请认真阅读并完成相应的任务．
题目：将分解因式
小彬解法：

……第1步
……………………………………第2步
……………………………第3步
小颖的解法：

……第1步
………………………第2步
………………………第3步
任务：
①经过讨论，他们发现两人中只有一人的解答正确，你认为解答正确的同学是______，这位同学的解答过程中第步依据的乘法公式可以用字母表示为______；而另一位同学的解答是从第______步开始出错的，你认为这位同学解答过程错误的原因是____________．
②按照做错同学的思路，写出正确的解答过程；
③除纠正上述错误外，请你根据平时的学习经验，在对多项式进行因式分解时还需要注意的事项给其他同学提一条建议．



21. 阅读理解：把4个数、、、排列成，我们称之为二阶行列式，规定其运算法则为，例如：．请解答下列各题：
（1）计算的值；
（2）若，求的值．




22. 数形结合是一种重要的数学思想方法，利用图中边长分别为、的两个正方形纸片和长为、宽为的长方形纸片，可以拼出一些图形来解释某些等式，如，由图可得．则：

（1）由图可以解释的等式是____________；
（2）用张边长为的正方形纸片，张长为、宽为的长方形纸片，张边长为的正方形纸片拼成一个大正方形，求这个大正方形的边长；
（3）用张长为，宽为的长方形纸片按照图方式不重叠地放在大长方形内，大长方形中未被覆盖的两个部分的面积设为、，的长设为．
①请用含的代数式表示：；
②若无论取任何实数时，①的结果始终保持不变，请直接写出与满足的数量关系．





23. 【问题背景】在学习了等腰三角形等有关知识后，数学活动小组发现：当角平分线遇上平行线时一般可得等腰三角形．如图1，为的角平分线上一点，常过点作交于点，易得为等腰三角形．

（1）【基本运用】如图2，把长方形纸片沿对角线折叠，使点落在点处，则重合部分是等腰三角形．请将以下过程或理由补充完整：
∵在长方形中，，
∴，由折叠性质可得：____________，
∴，
∴，（依据是：____________）
∴是等腰三角形；
（2）【类比探究】如图3，中，内角与外角的角平分线交于点，过点作分别交、于点、，试探究线段、、之间的数量关系并说明理由；
（3）【拓展提升】如图4，四边形中，，为边的中点，平分，连接，求证：．
参考答案
一、1~5：CDCBA 6~10：CDDAD
二、11.6 12. 13. 14. 15.9
三、16. 【小问1详解】
解：


．
【小问2详解】
解：



．
17.【小问1详解】
解：已知，，
∵，
∴；
∴的值是；
②，
∴的值是．
【小问2详解】
解：变形得，，
∴，
∴，解方程得，，
∴的值是．
18. （1）∴，
∴4＜5，
∴1＜﹣3＜2，
∴a＝1，b＝﹣4；
（2）（﹣a）3+（b+4）2＝（﹣1）3+（﹣4+4）2＝﹣1+17＝16，
∴（﹣a）3+（b+4）2的平方根是：±＝±4．
19. 证明：方法一∵，，若，
∴，
∴，
∴中，；
方法二：∵，，若，
∴，
∴，
∴中，；
方法三：∵，，若，
∴，
∴；
方法四：∵，，若，
∴，
∴
20. ①小彬的解法是根据完全平方公式展开，合并同类项，提取公因式，再根据平方差公式进行因式分解，各步骤严格按照因式分解法计算；小颖的解法是运用平方差公式进行因式分解，在第步的地方，忘记变号，故错误，
∴小彬的解法正确；
平方差公式用字母表示为：；
小颖的解法从第步出错，出错的原因是没有变号．
故答案为：小彬；；；没有变号；
②运用平方差公式正确的解法是：




；
③运用完全平方公式，平方差公式时，若是遇到多项式，要用括号括起来，再根据去括号法则去括号，注意各项的符号，合并同类项时，要根据有理数的加减法，合并同类项的法则进行．
21.【小问1详解】
解：，
∴的值为．
【小问2详解】
解：，
∵，即，
∴，
∴的值为．
22.【小问1详解】
解：大长方形的面积为：，两个小正方形（边长为），一个大正方形（边长为），三个长方形（长为、宽为）的面积和为：，
∵面积相等，
∴，
故答案为：．
【小问2详解】
解：张边长为的正方形纸片的面积为：，张长为、宽为的长方形纸片的面积为，张边长为的正方形纸片的面积为：，
∴拼成一个大正方形的面积为：，
∴大正方形的边长为：，
∵，，
∴，
∴，
∴∴大正方形的边长为．
【小问3详解】
解：①根据题意得，的长设为，
∴，，
∴，∴；
②无论取任何实数时，①的结果始终保持不变，
∴中含项的系数为零，
∴，即，
∴．
23. 【小问1详解】
证明：∵在长方形中，，
∴，由折叠性质可得，
∴，
∴，（依据是：等腰三角形中等角对等边）
∴是等腰三角形；
故答案为：；等腰三角形中等角对等边．
【小问2详解】
解：，理由如下，
由（1）可证，等腰三角形，则，
∵平方，，
∴，
∴为等腰三角形，即，
∵，
∴．
【小问3详解】
解：如图所示，过点作，

∵为边的中点，
∴点是的中点，即，
∵，平分，
∴，
∴是等腰三角形，即，
∴，
∴，
∵，
∴，
∴，
∵，
∴，即，
∴，
∴，
∴．