小学数学人教版三年级上册9 数学广角——集合教案设计

第九单元《数学广角——集合》

单元整体说明

“数学广角”这一单元介绍了一些数学思想方法，旨在让学生运用这些方法解决简单的实际问题或数学问题。本单元的主要学习内容是结合生活实例，让学生初步体会集合思想。

集合是现代数学的基本语言，可以简洁、准确地表达数学内容。集合思想是数学中的基本思想之一，是学生解决实际问题或数学问题应该掌握的重要数学思想。

学生从一年级学习数数时，就开始接触集合思想，在前面的学习过程中已经初步体会了集合元素之间建立的对应关系，对集合理论的基础——分类的思想方法也非常熟悉了。在此基础上介绍“思维图”表示集合及其运算方法，让学生体会集合的意义及集合的运算，学习用集合的思想方法思考和解决简单的实际问题，为今后的学习奠定基础。 本单元要用到的是含有重叠部分的集合图，对于这样的集合图，学生没有接触过。因此，教学时教师应首先让学生认识这些集合图，知道集合图每一部分表示的是什么。

集合

一、创设情境，导入新课

师：小熊开了一家文具店，店里的生意很好，很多商品都卖得很快，小熊这两天又进了不少货，大家请看一看，从图中我们发现小熊这两天进了几种商品？（课件出示）

教学提示：分组讨论，汇报成果， 教师巡视指导。

【学情预设】 共进了 7 种商品。

师：昨天和今天进的货中，有几种商品是重复的？

【学情预设】 3 种。

师：是哪三种呢？

【学情预设】 铅笔、钢笔、笔记本。

师：同学们真是火眼金睛啊，一下子就看出来了。重复又可以说成重叠，生活中重叠的现象有很多，这节课我们就来研究“重叠问题”。 （板书课题：集合）

设计意图：通过观察分析，引发学生思考，自然引入新课。

二、自主探索，互动授新

1.探究集合问题。

师：下面是三（1）班参加跳绳、踢毽比赛的学生名单。（课件出示）

师：大家观察一下，从表中你们获得了哪些信息？根据这些信息，你能提出一个数学问题吗？

教学提示：学生独立思考，举手发言，说说自己的发现，教师指导。要求学生表达要清 晰、完整，问题指向要明确。

【学情预设】 预设 1：参加跳绳比赛的有多少人？

预设2：参加踢毽比赛的有多少人？

预设3：参加跳绳比赛的比参加踢毽比赛的多多少人？

师：猜一猜，一共有多少人？

【学情预设】 预设1：17 人。

预设2：11 人。

预设3：14 人。

师：有同学猜 17 人，可是参加这两项比赛的没有 17 人呀！你发现了什么？

【学情预设】 这里面有学生重复了，有几人既参加了跳绳比赛，又参加了踢毽比赛。

师：那到底是几个人参加了两项比赛？有没有什么办法能使表中的信息变得更清楚呢？我们可以通过画一画、写一写等方式表示统计表中的信息，使大家看得更清楚，能够一眼就看出是哪些人参加了两项比赛，而哪些人只参加了其中一项。

【学情预设】 预设1：在表格中将重复的姓名连起来。（课件出示）

预设2：画交叉的图，表示重复的内容。

师：同学们画得都很好，我来用课件展示一下，看看你答对了吗？（课件出示）

【学情预设】 学生对比纠错。

师：同学们真棒，想到了这么多的方法来表达统计表中的信息。那这几种方式中你最喜欢哪一种？

【学情预设】 学生自由发言，表达自己的想法，说一说自己最喜欢的表达方式。

师：每种方法都有它的优点，都清楚地表示出了参加两项比赛的人。我们把所有踢毽的人看成一个整体，表示一个集合；同样地，我们把所有跳绳的人也看成一个整体，也表示一个集合。那右边的这个图表示什么？集合中内容是什么？填写的时候应当注意什么？按照什么顺序呢？

【学情预设】 学生根据自己的理解进行解答。

师：在数学上，常用这样的图直观地把集合中的具体事物表示出来，我们把它叫做维恩图。重叠的部分属于谁？表示什么？

【学情预设】 重叠的部分既属于左图，又属于右图，表示的是既参加了跳绳比赛，又参加了踢毽比赛的学生。

师：画维恩图时需要注意什么？

【学情预设】 预设1：用圈的形式把同类型的放在一起。

预设2：每幅图要标明里面是哪一类内容。

预设3：两个圈还可以合并在一起，重叠的部分就是两个圈重复的内容。

设计意图：让学生亲历整理过程，在这个过程中通过合作、思考、交流、比较等活动，让学生充分认识到重叠部分怎样做到既直观又美观，还能表示每部分的内容，让学生了解维恩图的同时，体会到数学文化的底蕴。

师：现在用维恩图来表示各项参赛的人数，与之前的表格比较，它有哪些优点？

【学情预设】 维恩图能直观看出参加各项运动的人数，尤其是重复参加两项比赛的人数。

师：应该怎样列式解答？

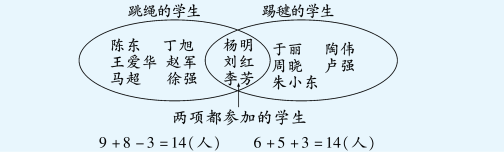
【学情预设】 预设1：6+3+5=14（人）。6是只参加跳绳的人数，3是两项都参加的人数，5是只参加踢毽的人数。

预设2：9+8-3=14（人）。9是参加跳绳的人数，8是参加踢毽的人数，有3人两项都参加了， 所以重复了，就要减一个3。

预设3：9+（8-3）=14（人）

预设4：8+（9-3）=14（人）

师：同学们真棒，用不同的方法解决了同一个问题，求出了两个集合的并集的元素个数。（板书算式）求两个集合的并集的元素个数，就是用两个集合的元素个数的和减去它们的交集的元素个数。

设计意图：让学生借助直观图，理解集合图的意义，并利用集合的思想方法解决简单的实际问题。让学生在不同的策略中感受到解决问题方法的多样性，提高思维水平和学习能力。

2.巩固练习，强化新知。

（1）完成教材第105页“做一做”第1题。

这道题，要求学生根据集合元素的特征填写维恩图，巩固对维恩图的认识，进一步体会集合概念的含义和交、并。突出强调中间部分表示什么，让学生用语言表达“既会游泳的，又会飞的”，加深对交集含义的认识。

（2）完成教材第105页“做一做”第2题。

学生先独立完成，再汇报交流。

师：你是用什么方法解答第一个问题的？要注意什么？

【学情预设】 圈出重复的姓名，再数出来。要认真仔细找，不要漏掉。

师：第二个问题要求什么？怎样解答？

学生独立完成，然后集体交流方法。

设计意图：这道题，从简单应用到开放，从正向思维到逆向思维，既链接所学知识资源， 又实现对学生思维的拓展。这样的练习设计不仅能让学生结合集合思想进行分析，还能结合可能性的知识解决问题。

三、课堂回顾，交流收获

师：通过本节课的学习，你又有哪些收获呢？

根据学生回答，教师小结：画图时先填中间的重复部分，剩下的再填左右两边的圈里。求事物的总数（两个计数部分有重复）时，先把两个计数部分相加，再减去重复部分。（同时出示课件）

四、作业设计，巩固提升

1.完成教材第106页“练习二十三”第2题。

通过填写维恩图及解决问题巩固对维恩图的认识及集合运算。

2.完成教材第107页“练习二十三”第5题。

通过练习脱离具体的元素，从集合元素个数的角度，进一步理解集合概念的含义和运算。

集合

集合是比较系统、抽象的数学思想方法，针对三年级学生的认知水平，在这里只是让学生通过生活中容易理解的题材去初步体会集合思想，为后继学习打下必要的基础，学生只要能够用自己的方法解决问题就可以了。在教学过程中，通过自主探究、小组讨论、合作交流的方式，调动了学生的积极性，使他们体会到了成功的快乐。“说一说、议一议、算一算、画一画”等丰富多彩的数学活动，充分调动了学生的多种感官协调合作， 让学生感悟了新知，发展了数感。课堂教学中，要注意抓住几个方面，一是创设情境，激发学生兴趣；二是建立认知冲突，初步画图；三是绘制集合图，理解重复现象。