




人教版五年级上册1 用字母表示数备课ppt课件
展开1.用含有字母的式子表示下面的数量关系。
(1)东方林场去年植树x棵,今年比去年多植树68棵,今年植树( )棵。(2)一个悠悠球a元,买5个悠悠球一共要支付( )元。(3)妈妈今年38岁,乐乐今年b岁,妈妈比乐乐大( )岁。(4)兰兰买3个练习本用去x元,每个练习本( )元。
18+29=29+ (23+39)+61=23+( + ) 15× =57× (3.6×1.5)×4=3.6×( × ) (40+8)× = ×2.5 + ×
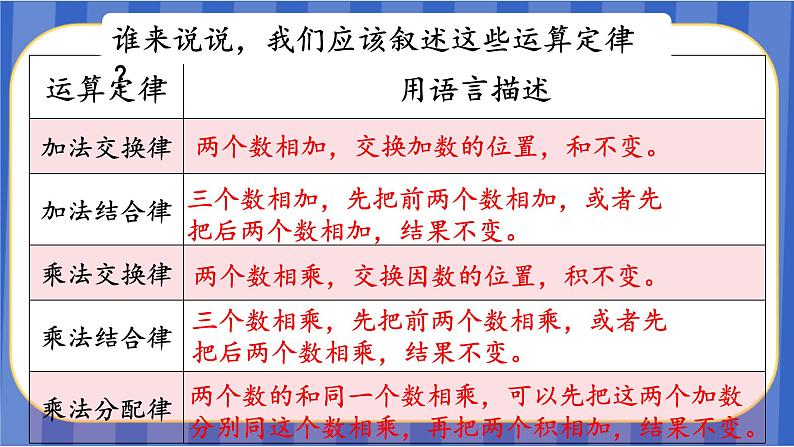
谁来说说,我们应该叙述这些运算定律?
两个数相加,交换加数的位置,和不变。
三个数相加,先把前两个数相加,或者先把后两个数相加,结果不变。
两个数相乘,交换因数的位置,积不变。
三个数相乘,先把前两个数相乘,或者先把后两个数相乘,结果不变。
两个数的和同一个数相乘,可以先把这两个加数分别同这个数相乘,再把两个积相加,结果不变。
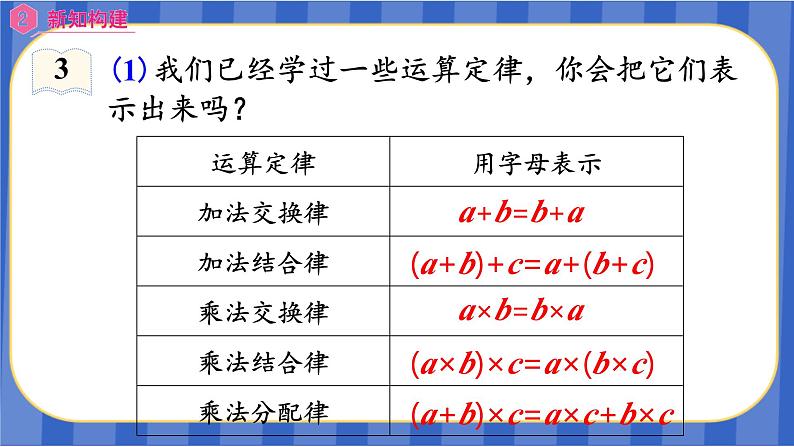
(a+b)+c=a+(b+c)
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
(1)我们已经学过一些运算定律,你会把它们表示出来吗?
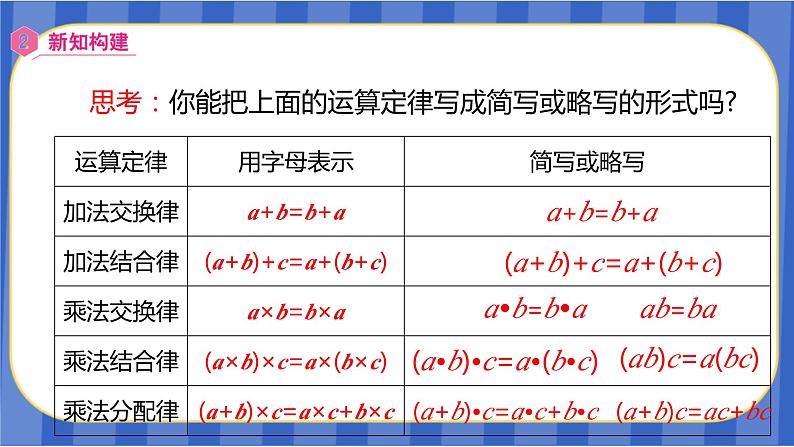
可以写成 a •b=b •a 或 ab=ba
注意:这种省略仅限于乘号,加、减、除号不能省略。
思考:你能把上面的运算定律写成简写或略写的形式吗?
(a•b)•c=a•(b•c)
(a+b)•c=a•c+b•c
(ab)c=a(bc)
(a+b)c=ac+bc
思考:其他的运算符号能省略吗?
思考:数字与数字之间的乘号能省略吗?为什么?
如:2×3中间的乘号省略了就会看成23了。
想一想,说一说:什么情况下乘号可以省略?
在含有字母的式子里,字母与字母相乘时,中间的乘号可以省略;m×n=mn数字与字母相乘时,中间的乘号可以省略;3×a=3a数字与数字相乘时,中间的乘号不能省略。其他的运算符号,例如“+”“-”“÷”等都不能省略。
α+b+c=α+(b+c)
α·b=b·α或αb=bα
(α·b)·c=α·(b·c)或(αb)c=α(bc)
(α+b)·c=α·c+b·c或(α+b)c=αc+bc
用字母表示运算定律跟用文字叙述相比有哪些好处?
用字母表示运算定律,更简明易记,也便于应用。
用字母表示:a-b-c = a-(b+c) = a-c-b
(1)从一个数里连续减去两个数,就等于减去这两个数的和;也可以先减去第二个数,再减去第一个数。
用字母可以表示一些运算的性质。
(2)n个数的和减去一个数,可以从任何一个加数里减去这个数(在能减的情况下),再同其余的加数相加。
用字母表示:(a+b+c)-d=(a-d)+b+c
(2)用字母表示出正方形的面积和周长。
正方形的面积=边长×边长
S = a•aS = a²
读作:a的平方,表示2个a相乘。
正方形的周长=边长×4
C = a•4C = 4a
省略乘号时,一般把数写在字母前面。
1.在含有字母的式子里,数字和字母中间的乘号可以记作“·” ,也可以省略不写。注意:数必须写在字母的前边。2.相同的两个字母a相乘,简写时一般不写成aa,而是写成a2 ,读作a的平方。
2a
这两个式子表示的意思一样吗?说说理由。
不一样,2a表示两个a相加,是a+a。
a²表示两个a相乘,是a×a。
请认真观察一下:a²的“ ² ”在大小上和位置上有什么特点?
1.a²不能写成a2哦!2.当a=5时,5×5就可以写成52。
a×a表示2个a相乘,写作a2 。a×a×a表示a×a×a×a×a×a表示
3个a相乘,写作a3,读作“a的立方”或“a的三次方”。
6个a相乘,写作a6,读作“a的六次方”。
计算下面正方形的面积和周长。
S=a2 =6×6 =36(cm2)
2.代入数据并还原乘号
3.算出结果,在后面加上单位
C=4a =__________ =__________
答:这个正方形的面积是 36 cm2, 周长是24 cm。
注意:在运算律中,字母可以表示任何数;但在面积、周长等公式中,字母的取值要符合实际情境,字母取值通常都大于0。应用公式求值解决问题的步骤: 第一步:写出字母公式 第二步:把字母表示的数值代入公式 代入数据只是用数据代替字母,原式中的运算顺序和运算符号是不变的。代入数据后要将乘号还原, 第三步:计算出结果,记住写单位
(教材第57页第10题)
长方形的周长=(长+宽)×2
(1)用字母表示出长方形的面积和周长。
S=
(2)一个长方形的长是 8 cm,宽是 5 cm,它的面积和周长各是多少?
S = ab = 8×5 = 40(cm²)
C = 2(a+b) = 2×(8+5) = 26(cm)
答:它的面积是40cm²,周长是26cm。
注意:在计算面积与周长时,要用字母表示的公式来算,这是和以前不同的。
1. 省略乘号写出下面各式。
(教材第56页第5题)
a×x x×x b×8 b×1
x²表示什么意思?和2x有什么区别?
不一样,x²表示的是两个x相乘;而2x表示的是两个x相加。
2. 把结果相等的两个式子连起来。
(教材第56页第6题)
一般情况下,一个数的平方和它的2倍是不相等的。只有当这个数等于0或2时,它们才相等。
3.判断。(1)x2表示两个x相乘。( )(2)因为8×a=8a,所以8×72的乘号可以省略不写。 ( )(3)c×3可以写成c3。( )(4)a2一定大于2a。( )(5)x+x+x=3+x。( )
4. 根据运算定律在 里填上适当的数或字母。
(教材第56页第7题)
a+(2+c)=( + )+ a • b • 4= • ( • ) 3x+5x=( + )• 4×(x+3)= × + ×
运算定律要记牢,字母和数一样看。
s = vt = 260×30=7800(米)
(1)用v表示速度,t表示时间,s表示路程。 s =_______
(2)如果每分钟行260m,时间是30分,路 程是多少米?
我每分钟骑v m。2分钟骑______m,t分钟骑______m。
答:路程是7800米。
(教材第57页第9题)
6. 用字母表示下面三角形的周长。
三角形的周长是三条边的和。
等边三角形,三条边相等。
等腰三角形,两腰相等。
一般三角形,三条边不相等。
如果 a = 8cm,等边三角形的周长是多少?
C = 3a = 3×8 = 24(cm)
答:等边三角形的周长是24cm。
7. 用 a 表示商品的单价,x 表示数量,c 表示总价,分别写出它们之间的数量关系:
如果每袋方便面 1.50 元, 6元可以买几袋?
答: 6元可以买4袋。
(教材第57页第11题)
王红每分钟打字50个,利用表中的公式计算她1小时打多少个字。
c=at =50×60 =3000(个)
答:她1小时打3000个字。
根据工作效率、工作时间和工作总量的关系可以填表。
(教材第57页第12题)
9.在右图中,(1)哪一部分的面积是ac?(2)哪一部分的面积是bc?
(教材第57页第13*题)
(3)整个图形的面积是多少?
长为a,宽为c,面积是ac。
长为b,宽为c,面积是bc。
用左边长方形的面积加右边长方形的面积
把整个图形看成是长(a+b),宽c的大长方形
答: (1)左边长方形长方形的面积是ac。 (2)右边长方形的面积是bc。 (3)整个图形的面积是(ac+bc)或(a+b)c。
10.如图,边长为b cm的大正方形中有一个边长a cm的小正方形。(1)图中涂色部分的面积是 cm²,周长是 cm。
(2)当a =10,b =23时,涂色部分的周长和面积分别是多少?
S涂色部分= S大正方形- S小正方形
当a =10,b =23时,
4b=4×23=92
b²-a²=23²-10²=23×23-10×10=429
答:涂色部分的周长是92cm,面积别是429cm²。
C涂色部分= C大正方形
1.运算定律、周长面积计算公式和常见的数量关系等 都可以用字母表示。2.用字母表示运算定律和计算公式,更简明易记,也 便于应用。
小学数学人教版五年级上册实际问题与方程试讲课备课课件ppt: 这是一份小学数学人教版五年级上册实际问题与方程试讲课备课课件ppt,共22页。PPT课件主要包含了已知条件,所求问题,怎样列方程呢,先找出等量关系,关键句,黑色皮,白色皮,还有其他等量关系吗,比黑色皮的2倍少4块,x-420等内容,欢迎下载使用。
小学数学解方程备课ppt课件: 这是一份小学数学解方程备课ppt课件,共28页。PPT课件主要包含了x38,x466,x18,x=11,=9+x,+x=20,+x-9=20-9,为什么要交换位置,这里为什么不减x,=9+x等内容,欢迎下载使用。
人教版五年级上册1 用字母表示数备课课件ppt: 这是一份人教版五年级上册1 用字母表示数备课课件ppt,共25页。PPT课件主要包含了x+2y,+10a,原有苹果质量,运来苹果质量,商店苹果总质量,每箱重akg,运来苹果10箱,=120+10×25,=120+250,=370等内容,欢迎下载使用。















