2024届高考数学一轮复习课时质量评价14含答案

这是一份2024届高考数学一轮复习课时质量评价14含答案，文件包含2024届高考数学一轮复习课时质量评价14docx、2024届高考数学一轮复习课时质量评价14含答案docx等2份试卷配套教学资源，其中试卷共6页， 欢迎下载使用。
课时质量评价(十四)A组　全考点巩固练1．D　解析：y为“小王从出发到返回原地所经过的路程”而不是位移，故排除A，C.又因为小王在乙地休息10分钟，排除B.故选D.2．B　解析：使用n天的平均耗资为＝元，当且仅当＝2n时取得最小值，此时n＝400.3．C　解析：由题意可知，m(t)＝＝0.1m0，则＝0.1，即－t＝ln 0.1≈－2.30，所以t≈184，则要使河水的污染水平下降到初始时的10%，需要的时间大约是184天，即半年．故选C.4．D　解析：设毛利润为L(p)元，则由题意知L(p)＝pQ－20Q＝Q(p－20)＝(8 300－170p－p2)(p－20)＝－p3－150p2＋11 700p－166 000，所以L′(p)＝－3p2－300p＋11 700. 令L′(p)＝0，解得p＝30或p＝－130(舍去)．当p∈(0，30)时，L′(p)>0；当p∈(30，＋∞)时，L′(p)<0.故L(p)在p＝30时取得极大值，即最大值，且最大值为L(30)＝23 000.5．8　解析：设至少过滤n次才能达到市场要求，则2%×≤0.1%，即，所以n lg ≤－1－lg 2，所以n≥7.39，所以n＝8.6．8　解析：由题知n≤log24 200＝ ＝.因为log210＝≈，0<log2<1，所以n≤8＋log2 ，n的最大值为8.B组　新高考培优练7．C　解析：设该污染物排放前过滤的次数为n(n∈N*)，由题意1.2×0.8n≤0.2，即≥6，两边取以10为底的对数可得lg ≥lg 6，即n lg ≥lg 2＋lg 3，所以n≥.因为lg 2≈0.3，lg 3≈0.477，所以≈＝7.77，所以n≥7.77，又n∈N*，所以nmin＝8，即该污染物排放前需要过滤的次数至少为8次．故选C.8．CD　解析：甲、乙、丙、丁的路程fi(x)(i＝1，2，3，4)关于时间x(x≥0)的函数关系式分别为f1(x)＝2x－1，f2(x)＝x2，f3(x)＝x，f4(x)＝log2(x＋1)，它们对应的函数模型分别为指数型函数模型、二次函数模型、一次函数模型、对数型函数模型．当x＝2时，f1(2)＝3，f2(2)＝4，所以A不正确；当x＝5时，f1(5)＝31，f2(5)＝25，所以B不正确．根据四种函数的变化特点，对数型函数的增长速度是先快后慢，又当x＝1时，甲、乙、丙、丁四个物体走过的路程相等，从而可知，当0<x<1时，丁走在最前面，当x>1时，丁走在最后面，所以C正确；指数型函数的增长速度是先慢后快，当运动的时间足够长时，最前面的物体一定是按照指数型函数模型运动的物体，即一定是甲物体，所以D正确．9．20　60　解析：设圆池的半径为r步，则方田的边长为(2r＋40)步，由题意，得(2r＋40)2－3r2＝13.75×240，解得r＝10或r＝－170(舍)，所以圆池的直径为20步，方田的边长为60步．10．解：(1)设服用1粒，经过x小时能有效抗病毒，即血液含药量需不低于4微克，可得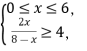解得≤x≤6.所以小时后该药能起到有效抗病毒的效果．(2)设经过x小时能有效抗病毒，即血液含药量需不低于4微克．若0≤x≤6，药物浓度≥4，解得≤x≤6.若6＜x≤12，药物浓度(12－x)＋≥4，解得x2－20x＋100≥0，所以6＜x≤12；若12＜x≤18，药物浓度12－(x－6)≥4，解得x≤14，所以12＜x≤14.综上，x∈，所以这次实验该药能够有效抗病毒的时间为小时．