2024届高考数学一轮复习课时质量评价21含答案

课时质量评价(二十一)

A组　全考点巩固练

1．AC　解析：因为角2α的终边在x轴的上方，所以k·360°＜2α＜k·360°＋180°，k∈Z，

则有k·180°＜α＜k·180°＋90°，k∈Z.

故当k＝2n，n∈Z时，n·360°＜α＜n·360°＋90°，n∈Z，α为第一象限角；

当k＝2n＋1，n∈Z时，n·360°＋180°＜α＜n·360°＋270°，n∈Z，α为第三象限角．故选AC.

2．C　解析：与角的终边相同的角是α＝＋2kπ，k∈Z，

所以当k＝－1时，α＝－.

3．D　解析：因为大轮有64齿，小轮有24齿，当大轮转动一周时，小轮转动的角度为2π×＝.

4．D　解析：由sin α＜0，得2kπ＋π＜α＜2kπ＋2π(k∈Z)，

所以kπ＋<<kπ＋π(k∈Z)，即是第二或第四象限角，所以tan ＜0.

5．－　解析：依题意，得cos α＝＝x<0，由此解得x＝－.

6．　解析：由题意知，点P，r＝1，所以点P在第四象限．根据三角函数的定义得cos α＝sin ＝，故α＝2kπ－(k∈Z)，所以α的最小正值为.

B组　新高考培优练

7．CD　解析：对于A，经过30分钟，钟表的分针转过－π弧度，不是π弧度，所以A错．对于B，1°化成弧度是rad，所以B错误．对于C，由sin θ＞0，可得θ为第一、第二及y轴正半轴上的角；由cos θ＜0，可得θ为第二、第三及x轴负半轴上的角．取交集可得θ是第二象限角，故C正确．对于D，若θ是第二象限角，所以2kπ＋＜θ＜2kπ＋π，则kπ＋＜＜kπ＋(k∈Z)．当k＝0或1时，得到为第一或第三象限角，故选项D正确．

8．C　解析：当t＝时，设点P在B处，当t＝时，设点P在C处，如图所示，

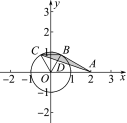
线段AP扫过形成图形为坐标系中的阴影部分，因为BC∥x轴，所以S△COB＝S△CAB，所以线段AP扫过形成图形的面积等于扇形BOC的面积，S扇形BOC＝×12×＝.故选C.

9．AC　解析：如果角α与γ＋45°终边相同，则α＝m·360°＋γ＋45°，m∈Z.

角β与γ－45°终边相同，则β＝n·360°＋γ－45°.n∈Z，

所以α－β＝m·360°＋γ＋45°－n·360°－γ＋45°＝(m－n)·360°＋90°(m∈Z，n∈Z)，

即α－β与90°角的终边相同，观察选项，选项AC符合题意．

10．

11．　解析：设截面圆的半径为R，连接CO，点D在线段CO上，

则AD＝AB＝10，

OD＝R－CD＝R－(20－10)．

根据垂径定理可得R2＝OD2＋AD2，解得R＝20，

所以∠AOD＝，则有∠AOB＝，

故可得弧长AB＝×20＝.

又木材的长为1米，即木材的长为100 cm，

所以该木材镶嵌在墙中的侧面积约为×100＝ (cm2).