2024届高考数学一轮复习课时质量评价59含答案

这是一份2024届高考数学一轮复习课时质量评价59含答案，文件包含2024届高考数学一轮复习课时质量评价59docx、2024届高考数学一轮复习课时质量评价59含答案docx等2份试卷配套教学资源，其中试卷共10页， 欢迎下载使用。
课时质量评价(五十九)1．某校开设a，b，c，d共4门选修课，一个同学从中随机选取2门，则a与b未同时被选中的概率为(　　)A．　 　 　    B．　 　 　    C．　 　 　    D．2．我国古代认为构成宇宙万物的基本要素是金、木、水、火、土这五种物质，称为“五行”．古人构建了金生水、水生木、木生火、火生土、土生金的相生理论，随机任取“两行”，则取出的“两行”相生的概率是(　　)A．    B．    C．    D．3．(多选题)从甲袋内摸出1个红球的概率是，从乙袋内摸出1个红球的概率是，从甲、乙袋内各摸出1个球，则(　　)A．2个球不都是红球的概率是B．2个球都是红球的概率是C．至少有1个红球的概率是D．2个球中恰有1个红球的概率是4．(2022·南京校级月考)十二生肖，又称十二属相，中国古人拿十二种动物来配十二地支，组成子鼠、丑牛、寅虎、卯兔、辰龙、巳蛇、午马、未羊、申猴、酉鸡、戌狗、亥猪十二属相．现有十二生肖吉祥物各一件，甲、乙、丙三位同学依次随机抽取一件作为礼物，甲同学喜欢马、牛，乙同学喜欢马、龙、狗，丙同学除了鼠不喜欢外其他的都喜欢，则这三位同学抽取的礼物都喜欢的概率是(　　)A．    B．    C．    D．5．某单位举行诗词大会比赛，给每位参赛者设计了“保留题型”“升级题型”“创新题型”三类题型，每类题型均指定一道题让参赛者回答．已知某位参赛者答对每道题的概率均为，且各次答对与否相互独立，则该参赛者答完三道题后至少答对两道题的概率为(　　)A．    B．    C．    D．6．已知甲、乙、丙、丁四人进行围棋比赛，比赛流程如图所示，根据以往经验，甲战胜乙、丙、丁的概率分别为0.8，0.4，0.6，丙战胜丁的概率为0.5，并且比赛没有和棋，则甲获得最后冠军的概率为(　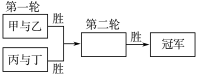　)A．0.6    B．0.5    C．0.4    D．0.37．某一大型购物广场有A，B两家奶茶店，某人第一天随机地选择一家奶茶店购买奶茶，如果第一天去A店，那么第二天去A店的概率为0.7；如果第一天去B店，那么第二天去A店的概率为0.6．则某人第二天去A店购买奶茶的概率为________．8．(2023·泰安模拟)某百科知识竞答比赛的半决赛阶段，每两人一组进行PK，胜者晋级决赛，败者终止比赛．比赛最多有三局．第一局限时答题，第二局快问快答，第三局抢答．比赛双方首先各自进行一局限时答题，依据答对题目数量，答对多者获胜，比赛结束，答对数量相等视为平局，则需进入快问快答局；若快问快答平局，则需进入抢答局，两人进行抢答，抢答没有平局．已知甲、乙两位选手在半决赛相遇，且在与乙选手的比赛中，甲限时答题局获胜与平局的概率分别为，，快问快答局获胜与平局的概率分别为，，抢答局获胜的概率为，且各局比赛相互独立．(1)求甲至多经过两局比赛晋级决赛的概率；(2)已知乙最后晋级决赛，但不知甲、乙两人经过几局比赛，求乙恰好经过三局比赛才晋级决赛的概率．         9．甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为与p，且乙投球2次均未命中的概率为．(1)求甲投球2次，至少命中1次的概率；(2)若甲、乙两人各投球2次，求两人共命中3次的概率．                B组　新高考培优练10．为了实施“科技下乡，精准脱贫”战略，某县科技特派员带着A，B，C三个农业扶贫项目进驻某村，对仅有的四个贫困户甲、乙、丙、丁进行产业帮扶．若每个贫困户只能选择一个扶贫项目，每个项目至少有一户选择，则甲、乙两户选择同一个扶贫项目的概率为(　　)A．    B．    C．    D．11．(2022·汕头二模)交通事故已成为世界性的严重社会问题，加强中小学生交通安全教育具有重要的现实意义，为此，某校举行了一场交通安全知识竞赛，一共有3道难度相当的必答题目，李明同学答对每道题目的概率都是0.6，则李明同学至少答对2道题的概率是(　　)A．0.36    B．0.576    C．0.648    D．0.90412．(多选题)根据中国古代重要的数学著作《孙子算经》记载，我国古代诸侯的等级自低到高分为：男、子、伯、侯、公五个等级．现有每个级别的诸侯各一人，君王要把50处领地全部分给5位诸侯，要求每位诸侯都分到领地且级别每高一级就多分m处(m为正整数)．按这种分法，下列结论正确的是(　　)A．为“男”的诸侯分到的领地不大于6处的概率是B．为“子”的诸侯分到的领地不小于6处的概率是C．为“伯”的诸侯分到的领地恰好为10处的概率是1D．为“公”的诸侯恰好分到16处领地的概率是13．袋中有黑球和白球共7个球，已知从中任取2个球都是白球的概率为．现有甲、乙两人从袋中轮流摸球(甲先)，每次摸出1球且不放回，直到摸出白球为止．则袋中原有白球的个数为________，甲摸到白球而终止的概率为________．14．某班甲、乙、丙、丁四名同学竞选班委，每个人是否当选相互独立，如果甲、乙两名同学都不当选的概率为，乙、丙两名同学都不当选的概率为，甲、丙两名同学都不当选的概率为，丁当选的概率为，则甲、乙、丙、丁四名同学中恰好有一人当选班委的概率是________．15．(2022·嘉兴期末)为了深入贯彻落实习近平总书记关于疫情防控的重要指示要求，某校组织开展“战‘疫’有我，青春同行”防控疫情知识竞赛活动，某班经过层层筛选后剩下甲、乙两名同学争夺一个参赛名额，该班设计了一个游戏方案决定谁去参加，规则如下：一个袋中装有6个大小相同的小球，其中标号为i的球有i个(i＝1，2，3)，甲、乙两名同学需从6个球中随机摸取3个球，所取球的标号之和多者获胜．(1)求甲所取球的标号之和为7的概率；(2)求甲获胜的概率．