2024届高考数学一轮复习第3章第2节第2课时导数与函数的极值、最值学案

这是一份2024届高考数学一轮复习第3章第2节第2课时导数与函数的极值、最值学案，共25页。学案主要包含了教材概念·结论·性质重现，基本技能·思想·活动经验等内容，欢迎下载使用。

一、教材概念·结论·性质重现
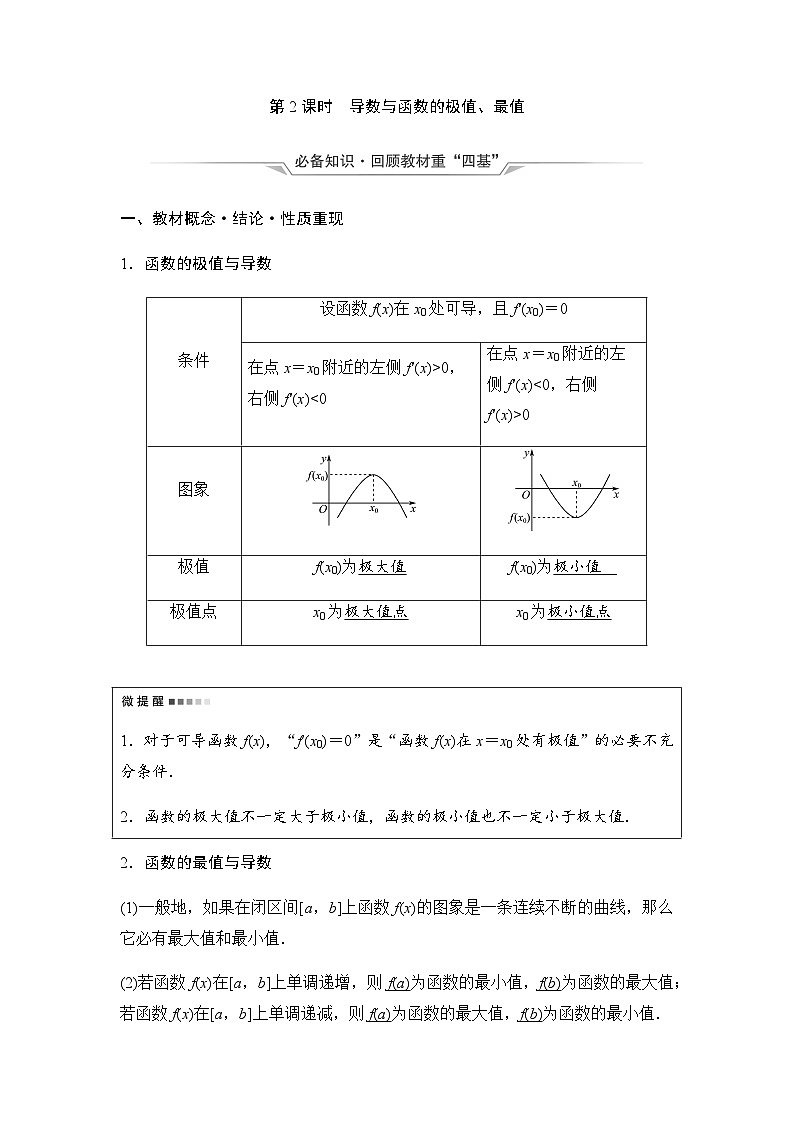
1．函数的极值与导数
1．对于可导函数f(x)，“f′(x0)＝0”是“函数f(x)在x＝x0处有极值”的必要不充分条件．
2．函数的极大值不一定大于极小值，函数的极小值也不一定小于极大值．
2．函数的最值与导数
(1)一般地，如果在闭区间[a，b]上函数f(x)的图象是一条连续不断的曲线，那么它必有最大值和最小值．
(2)若函数f(x)在[a，b]上单调递增，则f(a)为函数的最小值，f(b)为函数的最大值；若函数f(x)在[a，b]上单调递减，则f(a)为函数的最大值，f(b)为函数的最小值．
函数的极值是“局部”概念，函数的最值是“整体”概念，闭区间上函数的最值一定是极值或区间端点对应的函数值．
二、基本技能·思想·活动经验
1．判断下列说法的正误，对的画“√”，错的画“×”．
(1)函数的极大值不一定比极小值大．( √ )
(2)对可导函数f(x)，f′(x0)＝0是x0点为极值点的充要条件．( × )
(3)函数的极大值一定是函数的最大值．( × )
(4)开区间上的单调连续函数无最值．( √ )
2．函数y＝xex的最小值是( )
A．－1B．－e
C．－1eD．不存在
C 解析：因为y＝xex，所以y′＝ex＋xex＝(1＋x)ex.当x>－1时，y′>0；当x<－1时，y′<0，所以当x＝－1时，函数取得最小值，且ymin＝－1e.
3．函数y＝2x－1x2的极大值是_________．
－3 解析：函数y＝2x－1x2的定义域为(－∞，0)∪(0，＋∞)．y′＝2＋2x3，令y′＝0，得x＝－1.
当x<－1时，y′>0；当－10时，y′>0，
所以当x＝－1时，y取极大值－3.
4．若x＝1是函数f(x)＝x3＋ax的一个极值点，则实数a＝_________．
3 解析：f′(x)＝3x2－ax2，因为x＝1是f(x)的一个极值点，所以f′(1)＝3－a＝0，得a＝3.经检验，符合题意．
5．若函数f(x)＝13x3－4x＋m在[0，3]上的最大值为4，则m＝_________．
4 解析：f′(x)＝x2－4，x∈[0，3]，当x∈[0，2)时，f′(x)<0，当x∈(2，3]时，f′(x)>0，所以f(x)在[0，2)上单调递减，在(2，3]上单调递增．又f(0)＝m，f(3)＝－3＋m.所以在[0，3]上，fxmax＝f(0)＝4，所以m＝4.
考点1 利用导数求函数的极值——综合性
考向1 根据函数的图象判断函数的极值
(1)若函数f(x)，g(x)的导函数的图象分别如图(1)、图(2)所示，则f(x)与g(x)极值点的个数分别为( )
A．4，1B．2，2
C．4，2D．2，1
A 解析：对于可导函数，函数的极值点满足两个条件：一个是该点的导数为0，另一个是该点左右两侧的导数值异号．
由图象可知f(x)的导函数有4个零点，且4个零点的左右两侧的导数值异号，故f(x)有4个极值点；
由图象可知g(x)的导函数有两个零点，但只有一个零点的左右两侧的导数值异号，故g(x)有1个极值点．
(2)(2022·西安模拟)设函数f(x)在R上可导，其导函数为f′(x)且函数y＝(1－x)·f′(x)的图象如图所示，则下列结论一定成立的是( )
A．函数f(x)的极大值是 f(2)，极小值是f(1)
B．函数f(x)的极大值是 f(－2)，极小值是 f(1)
C．函数f(x)的极大值是 f(2)，极小值是 f(－2)
D．函数f(x)的极大值是f(－2)，极小值是 f(2)
D 解析：由函数的图象可知，f′(－2)＝0，f′(2)＝0，并且当x＜－2时，f′(x)＞0，当－2＜x＜1时，f′(x)＜0，故函数f(x)有极大值f(－2)．
又当1＜x＜2时，f′(x)＜0，当x＞2时，f′(x)＞0，故函数f(x)有极小值f(2)．
由图象判断函数y＝f(x)的极值的两个关注点
(1)由导函数y＝f′(x)的图象与x轴的交点，可得函数y＝f(x)的可能极值点．
(2)由导函数y＝f′(x)的图象可以看出y＝f′(x)的值的正负，进而可得函数y＝f(x)的单调性．
考向2 已知函数解析式求极值
(1)若函数f(x)＝x2ex的极大值点与极大值分别为a，b，则( )
A．a＜b＜abB．a＜ab＜b
C．b＜ab＜aD．ab＜b＜a
C 解析：f′(x)＝2xex-x2exe2x＝2x-x2ex，
易得，当x∈(0，2)时，f′(x)＞0，函数f(x)单调递增，当x∈(－∞，0)，(2，＋∞)时，f′(x)＜0，函数f(x)单调递减，故函数的极大值点a＝2，
所以b＝f(2)＝4e2，ab＝8e2，所以a＞ab＞b.
(2)已知函数f(x)＝lnxx－x，则( )
A．f(x)的单调递减区间为(0，1)
B．f(x)的极小值点为1
C．f(x)的极大值为－1
D．f(x)的最小值为－1
C 解析：函数f(x)的定义域为(0，＋∞)，f′(x)＝1-lnxx2－1＝1-lnx-x2x2，
令φ(x)＝1－ln x－x2，则φ′(x)＝－1x－2x<0，
所以φ(x)＝1－ln x－x2在(0，＋∞)上单调递减．
因为φ(1)＝0，所以当0＜x＜1时，φ(x)＞0；当x＞1时，φ(x)＜0，
所以f(x)的单调递增区间为(0，1)，单调递减区间为(1，＋∞)，
故f(x)的极大值点为1，f(x)极大值＝f(1)＝－1.
求函数f(x)极值的一般解题步骤
(1)确定函数的定义域．
(2)求导数f′(x)．
(3)解方程f′(x)＝0，求出函数定义域内的所有根．
(4)列表检验f′(x)在f′(x)＝0的根x0左右两侧值的符号．
(5)求出极值．
考向3 已知函数的极值求参数
(1)设函数f(x)＝exx+a，若f(x)的极小值为e，则a＝( )
A．－12B．12
C．32D．2
B 解析：函数f(x)＝exx+a的定义域为{x|x≠－a}．
f′(x)＝exx+a-exx+a2＝exx+a-1x+a2，
令f′(x)＝0，得x＝1－a，所以当x＜1－a且x≠－a时，f′(x)＜0；当x＞1－a时，f′(x)＞0，
所以f(x)在x＝1－a处取得极小值，所以f(1－a)＝e1-a＝e＝e12，所以1－a＝12，解得a＝12.
(2)(2021·全国乙卷)设a≠0，若x＝a为函数f(x)＝a(x－a)2(x－b)的极大值点，则( )
A．ab
C．aba2
D 解析：若a＝b，则f(x)＝a(x－a)3为单调函数，无极值点，不符合题意，故a≠b.
依题意，x＝a为函数f(x)＝a(x－a)2(x－b)的极大值点，
当a<0时，由x>b时，f(x)≤0，画出f(x)的图象如图所示：
由图可知ba2.
当a>0时，由x>b时，f(x)>0，画出f(x)的图象如图所示：
由图可知b>a，a>0，故ab>a2.综上所述，ab>a2成立．
根据函数极值情况求参数的2个要领
(1)列式：根据极值点处导数为0和极值这两个条件列方程组，利用待定系数法求解．
(2)验证：求解后验证根的合理性．
1．若函数f(x)＝(x2＋a)·ex的一个极值点为x＝1，则f(x)的极大值为( )
A．－3B．1
C．6e3D．－2e
C 解析： 因为f(x)＝(x2＋a)·ex，所以f′(x)＝(x2＋2x＋a)ex.
因为x＝1是f(x)的一个极值点，所以f′(1)＝(a＋3)e＝0，解得a＝－3.
当a＝－3时，f(x)＝(x2－3)·ex，f′(x)＝(x2＋2x－3)ex.
令f′(x)＞0，解得x＞1或x＜－3；
令f′(x)＜0，解得－3＜x＜1，
故f(x)在(－∞，－3)上单调递增，在(－3，1)上单调递减，在(1，＋∞)上单调递增，
故f(x)的极大值是f(－3)＝6e3.
2．已知函数f(x)＝x3－ax2－bx＋a2在x＝1处有极值10，则( )
A．a＝－4，b＝11
B．a＝3，b＝－3或a＝－4，b＝11
C．a＝－1，b＝5
D．以上都不正确
A 解析：函数的导数为f′(x)＝3x2－2ax－b.
因为函数f(x)＝x3－ax2－bx＋a2在x＝1处有极值10，
所以f(1)＝10且f′(1)＝0.
即3-2a-b=0， 1-a-b+a2=10，解得a=3，b=-3或a=-4，b=11.
当a＝3，b＝－3时，f′(x)＝3x2－6x＋3＝3(x－1)2≥0，
此时函数单调递增，函数没有极值，所以不满足条件．
经检验，当a＝－4，b＝11时，满足条件．
考点2 利用导数求函数的最值——综合性
(1)函数f(x)＝x ln x－x在12，2上的最小值为( )
A．－1+ln22B．－1
C．0D．2ln 2－2
B 解析：f(x)＝x ln x－x，x∈12，2，f′(x)＝ln x，
令f′(x)＞0，解得x＞1，
令f′(x)＜0，解得x＜1，
故f(x)在12，1上单调递减，在(1，2]上单调递增，故fxmin＝f(1)＝－1.
(2)(2021·新高考全国Ⅰ卷)函数f(x)＝2x-1－2ln x的最小值为_________．
1 解析：由题设知f(x)＝|2x－1|－2ln x的定义域为(0，＋∞)，
所以当0当12当x>1时，f(x)＝2x－1－2ln x，f′(x)＝2－2x>0，此时f(x)单调递增．
又f(x)在各分段的界点处连续，
综上，当01时，f(x)单调递增，
所以f(x)≥f(1)＝1.
本例(1)若把函数改为：f(x)＝x ln x，求函数f(x)在12，2上的最大值．
解：f(x)＝x ln x的定义域为(0，＋∞)，f′(x)＝ln x＋1.令f′(x)>0，得x>1e，
所以f(x)在1e，+∞上单调递增，
所以f(x)在12，2上单调递增，
所以f(x)max＝f(2)＝2ln 2.
求最值的3种情况
(1)若函数f(x)在区间[a，b]上单调递增或单调递减，f(a)与f(b)中有一个为最大值，另一个为最小值．
(2)若函数f(x)在闭区间[a，b]内有极值，要先求出[a，b]上的极值，与f(a)，f(b)比较，最大的是最大值，最小的是最小值，可列表完成．
(3)函数f(x)在区间(a，b)上有唯一一个极值点，这个极值点就是最大(或最小)值点．
1．(2022·全国甲卷) 当x＝1时，函数f(x)＝a ln x＋bx取得最大值－2，则f′(2)＝( )
A．－1B．－12
C．12D．1
B 解析：因为函数f(x)定义域为(0，＋∞)，所以依题可知，f(1)＝－2，f′(1)＝0，而f′(x)＝ax-bx2，所以b＝－2，a－b＝0，即a＝－2，b＝－2，所以f′(x)＝－2x+2x2，因此函数f(x)在(0，1)上单调递增，在(1，＋∞)上单调递减，x＝1时取最大值，满足题意，即有f′(2)＝－1＋12＝－12.故选B.
2．已知函数f(x)＝3-2xx2+a.
(1)若a＝0，求y＝f(x)在(1，f(1))处的切线方程；
(2)若函数f(x)在x＝－1处取得极值，求f(x)的单调区间，以及最大值和最小值．
解：(1)当a＝0时，f(x)＝3-2xx2，则f′(x)＝2x-3x3，所以f(1)＝1，f′(1)＝－4，
因此，曲线y＝f(x)在点(1，f(1))处的切线方程为y－1＝－4(x－1)，即4x＋y－5＝0.
(2)因为f(x)＝3-2xx2+a，则f′(x)＝-2x2+a-2x3-2xx2+a2＝2x2-3x-ax2+a2.
由题意可得f′(－1)＝24-aa+12＝0，解得a＝4，经检验，符合题意．
故f(x)＝3-2xx2+4，f′(x)＝2x+1x-4x2+42.
列表如下：
所以，函数f(x)的单调递增区间为(－∞，－1)，(4，＋∞)，单调递减区间为(－1，4)．
当x<32时，f(x)>0；当x>32时，f(x)<0.
所以f(x)max＝f(－1)＝1，f(x)min＝f(4)＝－14.
考点3 极值与最值的综合应用——综合性
(1)(多选题)(2022·新高考Ⅰ卷)已知函数f(x)＝x3－x＋1，则( )
A．f(x)有两个极值点
B．f(x)有三个零点
C．点(0，1)是曲线y＝f(x)的对称中心
D．直线y＝2x是曲线y＝f(x)的切线
AC 解析：由题，f′(x)＝3x2－1，令f′(x)>0，得x>33或x<－33，
令f′(x)<0得－33因f-33＝1＋239>0，f33＝1－239>0，f(－2)＝－5<0，
所以函数f(x)在-∞，-33上有一个零点，
当x≥33时，f(x)≥f33>0，即函数f(x)在33，+∞上无零点，
综上所述，函数f(x)有一个零点，故B错误；
令h(x)＝x3－x，该函数的定义域为R，h(－x)＝(－x)3－(－x)＝－x3＋x＝－h(x)，
则h(x)是奇函数，(0，0)是h(x)的对称中心，
将h(x)的图象向上移动一个单位得到f(x)的图象，
所以点(0，1)是曲线y＝f(x)的对称中心，故C正确；
令f′(x)＝3x2－1＝2，可得x＝±1，又f(1)＝f(－1)＝1，
当切点为(1，1)时，切线方程为y＝2x－1，当切点为(－1，1)时，切线方程为y＝2x＋3，故D错误．故选AC.
(2)已知函数f(x)＝ax2+bx+cex(a>0)的导函数y＝f′(x)的两个零点为－3和0.
①求f(x)的单调区间；
②若f(x)的极小值为－e3，求f(x)在区间[－5，＋∞)上的最大值．
解：①f′(x)＝2ax+bex-ax2+bx+cexex2＝-ax2+2a-bx+b-cex.
令g(x)＝－ax2＋(2a－b)x＋b－c，
因为ex>0，所以y＝f′(x)的零点就是g(x)＝-ax2＋(2a－b)x＋b－c的零点，且f′(x)与g(x)符号相同．又因为a>0，所以当－30，即f′(x)>0；
当x<－3或x>0时，g(x)<0，即f′(x)<0，
所以f(x)的单调递增区间是(－3，0)，
单调递减区间是(－∞，－3)，(0，＋∞)．
②由①知，x＝－3是f(x)的极小值点，
所以有9a-3b+ce-3=-e3， g0=b-c=0， g-3=-9a-32a-b+b-c=0，
解得a＝1，b＝5，c＝5，所以f(x)＝x2+5x+5ex.
因为f(x)的单调递增区间是(－3，0)，单调递减区间是(－∞，－3)，(0，＋∞)，
所以f(0)＝5为函数f(x)的极大值，
故f(x)在区间[－5，＋∞)上的最大值取f(－5)和f(0)中的最大者．而f(－5)＝5e-5＝5e5>5＝f(0)，
所以函数f(x)在区间[－5，＋∞)上的最大值是5e5.
求极值、最值时，要求步骤规范、表格齐全．函数在给定闭区间上存在极值，一般要将极值与端点值进行比较才能确定最值，不能想当然地认为极值点就是最值点．含参数时，要讨论参数的大小．
1．已知函数f(x)＝－x3＋ax2－4在x＝2处取得极值，若m，n∈[－1，1]，则f(m)＋f′(n)的最小值是( )
A．－13B．－15
C．10D．15
A 解析：对函数f(x)求导得f′(x)＝－3x2＋2ax，
由函数f(x)在x＝2处取得极值知f′(2)＝0，
即－3×4＋2a×2＝0，所以a＝3.
由此可得f(x)＝－x3＋3x2－4，f′(x)＝－3x2＋6x.
易知f(x)在[－1，0)上单调递减，在[0，1]上单调递增，
所以当m∈[－1，1]时，f(m)min＝f(0)＝－4.
又因为f′(x)＝－3x2＋6x的图象开口向下，
且对称轴为x＝1，所以当n∈[－1，1]时，
f′(n)min＝f′(－1)＝－9.
故f(m)＋f′(n)的最小值为－13.
2．已知函数f(x)＝ax2＋b ln x在x＝1处有极值12.
(1)求a，b的值；
(2)求函数f(x)在12，2上的最大值与最小值．
解：(1)由题可知，f(x)＝ax2＋b ln x，f(x)的定义域为(0，＋∞)，
所以f′(x)＝2ax＋bx(x>0)．
由于f(x)在x＝1处有极值12，
则f1=a+ln1=12，f'1=2a+b=0，
即a=12， 2a+b=0，
解得a＝12，b＝－1.
(2)由(1)可知f(x)＝12x2－ln x，其定义域是(0，＋∞)，f′(x)＝x－1x＝x+1x-1x.
令f′(x)＝0，而x>0，解得x＝1.
由f′(x)<0，得00，得x>1，
则在区间12，2上，x，f′(x)，f(x)的变化情况表如下：
可得f(x)min＝f(1)＝12，
f12＝18＋ln 2，f(2)＝2－ln 2.
由于f(2)－f12＝2－ln 2－18+ln2>0，则f(2)>f12，所以f(x)max＝f(2)＝2－ln 2.
所以函数f(x)在区间12，2上的最大值为2－ln 2，最小值为12.
课时质量评价(十七)
A组 全考点巩固练
1．(2023·辽宁月考)函数f(x)的定义域为R，它的导函数y＝f′(x)的部分图象如图所示，则下面结论正确的是( )
A．函数f(x)在(1，2)上为减函数
B．函数f(x)在(3，5)上为增函数
C．函数f(x)在(1，3)上有极大值
D．x＝3是函数f(x)在区间[1，5]上的极小值点
C 解析：由y＝f′(x)的部分图象可知，
当1＜x＜2时，f′(x)＞0，则f(x)单调递增；
当2＜x＜4时，f′(x)＜0，则f(x)单调递减；
当4＜x＜5时，f′(x)＞0，则f(x)单调递增．
又f′(2)＝f′(4)＝0，所以当x＝2时，f(x)取得极大值；当x＝4时，f(x)取得极小值．故选C.
2．函数f(x)的导函数为 f′(x)＝－x(x＋2)，则函数f(x)有( )
A．最小值f(0)B．最小值f(－2)
C．极大值f(0)D．极大值f(－2)
C 解析：令f′(x)＝－x(x＋2)＞0，解得－2＜x＜0，即函数的单调递增区间为(－2，0)；
令f′(x)＝－x(x＋2)＝0，解得x＝－2或x＝0；
令f′(x)＝－x(x＋2)＜0，解得x＞0或x＜－2，即函数的单调递减区间为(－∞，－2)，(0，＋∞)，所以函数的极大值为f(0)．
3．(2022·宿州期中)已知函数f(x)＝e2-x＋x，x∈[1，3]，则下列说法正确的是( )
A．函数f(x)的最小值为3＋1e
B．函数f(x)的最大值为3＋1e
C．函数f(x)的最小值为e＋1
D．函数f(x)的最大值为e＋1
D 解析：f(x)＝e2-x＋x，f′(x)＝－e2-x＋1，
令f′(x)＞0，解得x＞2，
令f′(x)＜0，解得x＜2，
故f(x)在[1，2)上单调递减，在(2，3]上单调递增，故f(x)的最小值是f(2)＝3，
f(1)＝e＋1，f(3)＝3＋1e.
因为3＋1e－(e＋1)＝2＋1e－e<2＋12－e<0，所以函数f(x)的最大值为1＋e.
4．已知函数f(x)＝lnxx－ex，则下列说法正确的是( )
A．f(x)无极大值，也无极小值
B．f(x)有极大值，也有极小值
C．f(x)有极大值，无极小值
D．f(x)无极小值，有极大值
C 解析：由题意得f′(x)＝1-lnx-x2exx2，x＞0，
令g(x)＝1－ln x－x2ex，则g′(x)＝－1x－2xex－x2ex＜0，
所以g(x)单调递减．又g1e＞0，g(1)＜0，
所以∃x0∈1e，1，使g(x0)＝0，
所以当x∈(0，x0)时，g(x)＞0，f′(x)＞0，f(x)单调递增；
当x∈(x0，＋∞)时，g(x)＜0，f′(x)＜0，f(x)单调递减．
所以f(x)有极大值，无极小值，故C正确．
5．已知函数f(x)＝x2e1-x－a有三个零点，则实数a的取值范围是( )
A．0，2eB．0，4e
C．0，2e2D．0，4e2
B 解析：由f(x)＝x2e1-x－a＝0有三个零点得a＝x2e1-x有三个零点．
设g(x)＝x2e1-x，则g′(x)＝e1-xx(2－x)，
当x＜0时，g′(x)＜0，函数单调递减；当0＜x＜2时，g′(x)＞0，函数单调递增；当x＞2时，g′(x)＜0，函数单调递减．
因为g(0)＝0，g(2)＝4e，所以0＜a＜4e.
6．已知函数f(x)＝x(x－c)2在x＝2处有极大值，则c＝_________．
6 解析：因为f′(x)＝(x－c)2＋2x(x－c)＝3x2－4cx＋c2，且函数f(x)＝x(x－c)2在x＝2处有极大值，所以f′(2)＝0，即c2－8c＋12＝0，解得c＝6或2.经检验c＝2时，函数f(x)在x＝2处取得极小值，不符合题意，应舍去．故c＝6.
7．(2023·滨州月考)用长为18 cm的钢条围成一个长方体形状的框架，要求长方体的长与宽之比为2∶1，设该长方体的宽为x cm，当x＝________时，其体积最大，最大体积是________ cm3.
1 3 解析：长方体的宽为x cm，则长为2x cm，高为18-8x-4x4 cm.
长方体的体积为V(x)＝2x·x·92-3x＝9x2－6x3其中0＜x＜32，
V′(x)＝18x－18x2，令V′(x)＝0，得18x－18x2＝0，解得x＝0(舍去)或x＝1.
当0＜x＜1时，V′(x)＞0，函数V(x)单调递增，当1＜x＜32时，V′(x)＜0，函数V(x)单调递减．所以当x＝1时，函数V(x)有最大值3 cm3.
8．已知函数f(x)＝ex1+ax2，其中a为正实数，x＝12是f(x)的一个极值点．
(1)求a的值；
(2)当b＞12时，求函数f(x)在[b，＋∞)上的最小值．
解：f′(x)＝ax2-2ax+1ex1+ax22，
(1)因为x＝12是函数y＝f(x)的一个极值点，所以f′12＝0，
因此，14a－a＋1＝0，解得a＝43，
经检验，当a＝43时，x＝12是y＝f(x)的一个极值点，故所求a的值为43.
(2)由(1)可知，f′(x)＝43x2-83 x+1ex1+43x22，
令f′(x)＝0，得x1＝12，x2＝32.
f(x)与f′(x)的变化情况如下：
所以，f(x)的单调递增区间是-∞，12，32，+∞，单调递减区间是12，32.
当12＜b＜32时，f(x)在b，32上单调递减，在32，+∞上单调递增，
所以f(x)在[b，＋∞)上的最小值为f32＝ee4，
当b≥32时，f(x)在[b，＋∞)上单调递增，
所以f(x)在[b，＋∞)上的最小值为f(b)＝eb1+ab2＝3eb3+4b2.
B组 新高考培优练
9．已知函数f(x)的定义域为D，其导函数为f′(x)，函数y＝sin x·f′(x)(x∈D)的图象如图所示，则f(x)( )
A．有极小值f(2)，极大值f(π)
B．有极大值f(2)，极小值f(0)
C．有极大值f(2)，无极小值
D．有极小值f(2)，无极大值
D 解析：当x∈(0，π)时，sin x＞0，当x∈(π，2π)时，sin x＜0.
由图象可得当x∈(0，2)时，f′(x)≤0，当x∈(2，π)时，f′(x)>0，
当x∈(π，2π)时，f′(x)≥0，故函数f(x)在(0，2)上单调递减，在(2，π)上单调递增，在(π，2π)上单调递增，所以f(x)在定义域D上，先减后增，有极小值f(2)，无极大值．
10．函数f(x)＝ln x＋12x2－ax(x＞0)在区间12，3上有且仅有一个极值点，则实数a的取值范围是( )
A．52，3B．52，103
C．52，103D．2，103
B 解析：f′(x)＝1x＋x－a，依题意，y＝f′(x)在区间12，3上有且仅有一个变号零点，令f′(x)＝0，则a＝x＋1x，令g(x)＝x＋1x，x∈(0，＋∞)．
由双勾函数的性质可知，函数g(x)在(0，1)上单调递减，在(1，＋∞)上单调递增，
所以g(x)min＝g(1)＝2.又g12＝g(2)＝52，g(3)＝103.
结合g(x)＝x＋1x在(0，＋∞)上的图象可得，52≤a<103.
11．(多选题)(2022·新高考Ⅰ卷) 已知函数f(x)及其导函数f′(x)的定义域均为R，记g(x)＝f′(x)，若f32-2x，g(2＋x)均为偶函数，则( )
A．f(0)＝0B．g-12＝0
C．f(－1)＝f(4)D．g(－1)＝g(2)
BC 解析：因为f32-2x，g(2＋x)均为偶函数，
所以f32-2x＝f32+2x，即f32-x＝f32+x，g(2＋x)＝g(2－x)，
所以f(3－x)＝f(x)，g(4－x)＝g(x)，则f(－1)＝f(4)，故C正确；
函数f(x)，g(x)的图象分别关于直线x＝32，x＝2对称，
又g(x)＝f′(x)，且函数f(x)可导，所以g32＝0，g(3－x)＝－g(x)，
所以g(4－x)＝g(x)＝－g(3－x)，所以g(x＋2)＝－g(x＋1)＝g(x)，
所以g-12＝g32＝0，g(－1)＝g(1)＝－g(2)，故B正确，D错误；
若函数f(x)满足题设条件，则函数f(x)＋C(C为常数)也满足题设条件，所以无法确定f(x)的函数值，故A错误．故选BC.
12．写出一个定义在R上且使得命题“若f′(1)＝0，则1为函数f(x)的极值点”为假命题的函数f(x)＝___________．
(x－1)3(不唯一) 解析：函数f(x)＝(x－1)3，则f′(x)＝3(x－1)2，故 f′(1)＝0.
又f′(x)＝3(x－1)2≥0在R上恒成立，故f(x)在R上为增函数，
所以x＝1不是f(x)＝(x－1)3的极值点．
13．对于函数f(x)＝ln x＋mx2＋nx＋1，有下列4个论断：
甲：函数f(x)有两个减区间；
乙：函数f(x)的图象过点(1，－1)；
丙：函数f(x)在x＝1处取极大值；
丁：函数f(x)单调．
若其中有且只有两个论断正确，则m的取值为_________．
2 解析：函数f(x)的定义域是(0，＋∞)，由题意得：f′(x)＝1x＋2mx＋n＝2mx2+nx+1x，
令g(x)＝2mx2＋nx＋1，显然g(x)过定点(0，1)．
①m＞0时的图象可能是：
或
②m＜0时的图象可能是：
或
当x＞0时，函数f(x)最多有1个减区间，故甲错误；
假设乙正确，则f(1)＝m＋n＋1＝－1，即m＋n＝－2，
此时f′(x)＝2x-1mx-1x，若丙正确，则解得m＝1，故n＝－3，
而此时f(x)在x＝1处取极小值，即与丙、丁矛盾；
若丁正确，则m＝2，n＝－4，可满足题意．
综上，乙、丁正确，且m＝2.
14．(2022·中卫三模)已知函数f(x)＝exx2＋2k ln x－kx，若x＝2是函数f(x)的唯一一个极值点，则实数k的取值范围是___________．
-∞，e24 解析：因为函数f(x)的定义域是(0，＋∞)，
所以f′(x)＝exx-2x3+2kx－k＝ex-kx2x-2x3.
因为x＝2是函数f(x)的唯一一个极值点，
所以x＝2是导函数f′(x)＝0的唯一根，
所以ex－kx2＝0在(0，＋∞)上无变号零点，
即k＝exx2在x＞0上无变号零点．
令g(x)＝exx2，
因为g′(x)＝exx-2x3，
所以g(x)在(0，2)上单调递减，在x＞2 上单调递增，
所以g(x)的最小值为g(2)＝e24，所以必须k≤e24.
15．(2023·济宁模拟)已知函数f(x)＝12x2－(m＋1)x＋ln x(m∈R)．
(1)讨论函数f(x)的单调性；
(2)若f(x)有两个极值点x1，x2，且x1＜x2，当m≤73时，求f(x1)－f(x2)的取值范围．
解：(1)f(x)的定义域为(0，＋∞)，
f′(x)＝x＋1x－(m＋1)＝x2-m+1x+1x，令g(x)＝x2－(m＋1)x＋1(该函数与f′(x)同号)，当m＋1≤0，即m≤－1时，f′(x)＞0在(0，＋∞)上恒成立，故此时f(x)是增函数；当m+1＞0， m+12-4＞0，即m＞1时，g(x)＝0有两个正根，x1＝m+1-m2+2m-32，x2＝m+1+m2+2m-32，显然x1＜x2，
此时f(x)的单调递增区间为(0，x1)，(x2，＋∞)，单调递减区间为(x1，x2)；
同理当－1＜m≤1时，f′(x)≥0在(0，＋∞)上恒成立，故此时f(x)是增函数．
综上可知：当m≤1时，f(x)在(0，＋∞)上是增函数；当m＞1时，g(x)＝0的两根为x1＝m+1-m2+2m-32，x2＝m+1+m2+2m-32，此时f(x)的单调递增区间为(0，x1)，(x2，＋∞)，单调递减区间为(x1，x2)．
(2)由(1)知，f′(x)＝x＋1x－(m＋1)＝x2-m+1x+1x，再令g(x)＝x2－(m＋1)x＋1，
当m＞1，f(x)的两个极值点为g(x)＝0的两个互异的正实根x1，x2，
且x1＋x2＝m＋1，x1·x2＝1，则x1＋1x1＝m＋1∈2，103，即2＜x1＋1x1≤103，
显然x1≠1，由x1＋1x1≤103整理得3x12－10x1＋3≤0，解得13≤x1≤3，且x1≠1，
因为0＜x1＜x2，x1·x2＝1，
所以13≤x1＜1，
而f(x1)－f(x2)＝12x12-x22＋(m＋1)(x2－x1)＋ln x1－ln x2，
将x1＋x2＝m＋1代入上式整理得f(x1)－f(x2)＝-12x12-x22＋ln x1－ln x2，
再将x2＝1x1代入上式得：
f(x1)－f(x2)＝-12x12+12x12＋2ln x1，13≤x1<1，
令h(x)＝－12x2＋12x2＋2ln x，13≤x＜1，
h′(x)＝－x－1x3+2x＜0在x∈13，1上恒成立，故h(x)在13，1上单调递减，
h(x)max＝h13＝409－2ln 3，h(x)min＞h(1)＝0，且h(x)≠0，
即f(x1)－f(x2)的取值范围为0，409-2ln3.
条件
设函数f(x)在x0处可导，且f′(x0)＝0
在点x＝x0附近的左侧f′(x)>0，右侧f′(x)<0
在点x＝x0附近的左侧f′(x)<0，右侧f′(x)>0
图象
极值
f(x0)为极大值
f(x0)为极小值__
极值点
x0为极大值点
x0为极小值点
x
(－∞，－1)
－1
(－1，4)
4
(4，＋∞)
f′(x)
＋
0
－
0
＋
f(x)
单调递增
极大值
单调递减
极小值
单调递增
x
12
12，1
1
(1，2)
2
f′(x)
－
0
＋
f(x)
18＋ln 2
单调递减
12
单调递增
2－ln 2
x
-∞，12
12
12，32
32
32+∞
f′(x)
＋
0
－
0
＋
f(x)

3e4

ee4
