人教版九年级数学上册同步精品讲义 第二十三章 旋转单元检测（2份打包，原卷版+教师版）

这是一份人教版九年级数学上册同步精品讲义 第二十三章 旋转单元检测（2份打包，原卷版+教师版），文件包含人教版九年级数学上册同步精品讲义第二十三章旋转单元检测教师版doc、人教版九年级数学上册同步精品讲义第二十三章旋转单元检测原卷版doc等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。

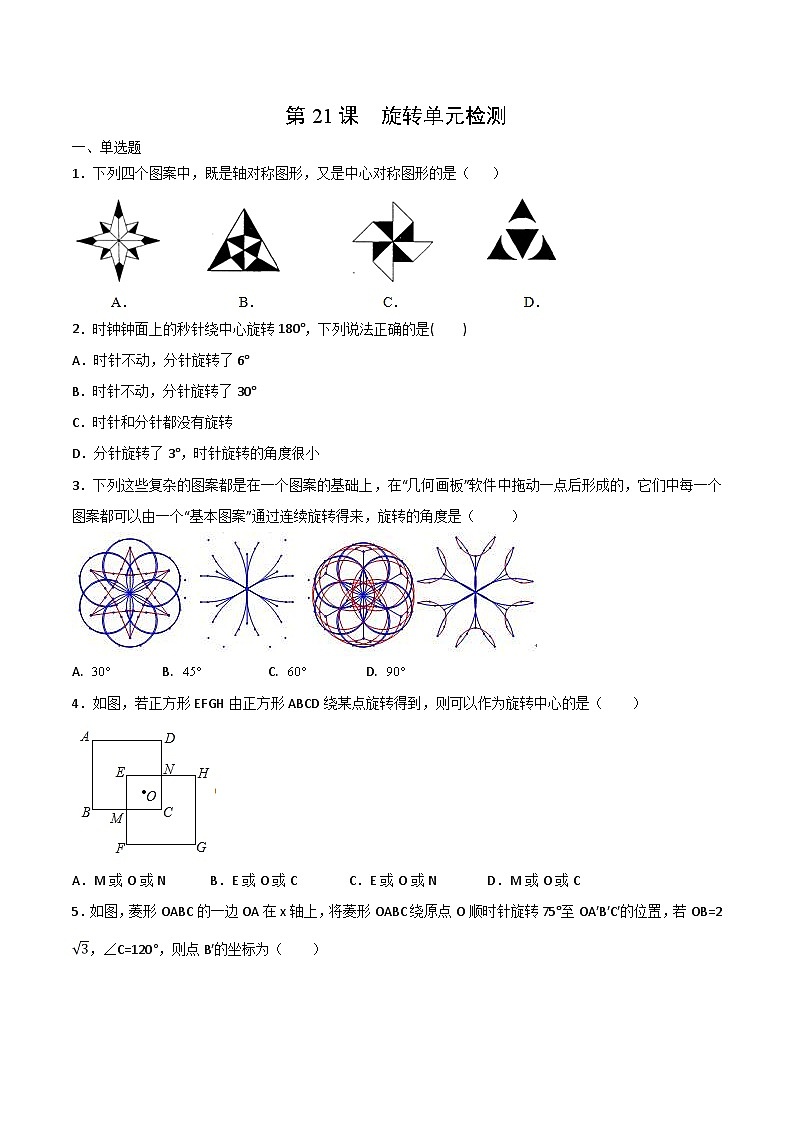
第21课 旋转单元检测
一、单选题
1．下列四个图案中，既是轴对称图形，又是中心对称图形的是（ ）

2．时钟钟面上的秒针绕中心旋转180°，下列说法正确的是(　　)
A．时针不动，分针旋转了6°
B．时针不动，分针旋转了30°
C．时针和分针都没有旋转
D．分针旋转了3°，时针旋转的角度很小
3．下列这些复杂的图案都是在一个图案的基础上，在“几何画板”软件中拖动一点后形成的，它们中每一个图案都可以由一个“基本图案”通过连续旋转得来，旋转的角度是（ ）

A. B. C. D.
4．如图，若正方形EFGH由正方形ABCD绕某点旋转得到，则可以作为旋转中心的是（　　）

A．M或O或N B．E或O或C C．E或O或N D．M或O或C
5．如图，菱形OABC的一边OA在x轴上，将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置，若OB=2，∠C=120°，则点B′的坐标为（　　）

A．（3，） B．（3，） C．（，） D．（，）
6．如图，Rt△ABC中，∠ACB＝90°，∠B＝30°，S△ABC＝，将△ABC绕点C逆时针旋转至△A′B′C，使得点A'恰好落在AB上，A'B′与BC交于点D，则S△A′CD为（ ）

A． B． C． D．
7．如图，将斜边长为4的直角三角板放在直角坐标系xOy中，两条直角边分别与坐标轴重合，P为斜边的中点．现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是（ ）

A．（，1） B．（1，﹣） C．（2，﹣2） D．（2，﹣2）
8．已知，将点A1（4，2）向左平移3个单位到达点A2的位置，再向上平移4个单位到达点A3的位置，△A1A2A3绕点A2逆时针方向旋转90°，则旋转后A3的坐标为（　　）
A． B． C． D．
二、填空题
9．如图，△ABC是等腰直角三角形，BC是斜边，P为△ABC内一点，将△ABP绕点A逆时针旋转后与△ACP′重合，若AP=1，那么线段PP′的长等于_____．

10．如图，已知Rt△ABC中，∠ACB=90°，AC=6，BC=4，将△ABC绕直角顶点C顺时针旋转90°得到△DEC．若点F是DE的中点，连接AF，则AF= ．

11．将一个正六边形绕着其中心，至少旋转 度可以和原来的图形重合．
12．如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=3，∠BCD=45°，将腰CD以点D为中心逆时针旋转90°至ED，连结AE，CE，则△ADE的面积是_____．

13．如图，中，，，，把绕着它的斜边中点逆时针旋转至的位置，交于点．与重叠部分的面积为________．

14．如图，正方形ABCD的边长为4cm，正方形AEFG的边长为1cm．如果正方形AEFG绕点A旋转，那么C、F两点之间的最小距离为_________cm．

15．如图，在直角坐标系中，已知点P0的坐标为（1，0），进行如下操作:将线段OPo按逆时针方向旋转，再将其长度伸长为OP0的2倍，得到线段OP1 ；又将线段OP1按逆时针方向旋转，长度伸长为OP1的2倍，得到线段OP2，如此重复操作下去，得到线段OP3，OP4，， 则

（1）点P5的坐标为
（2）落在x轴正半轴上的点Pn坐标是 ，（ n是8的整数倍.）
三、解答题
16．如图所示，点P是正方形ABCD内的一点，连接AP，BP，CP，将△PAB绕着点B顺时针旋转90°到△P′CB的位置．若AP=2，BP=4，∠APB=135°，求PP′及PC的长．

17．如图，将两块直角三角尺的60°角和90°角的顶点A叠放在一起．将三角尺ADE绕点A旋转，旋转过程中三角尺ADE的边AD始终在∠BAC的内部在旋转过程中，探索：
（1）∠BAE与∠CAD的度数有何数量关系，并说明理由；
（2）试说明∠CAE﹣∠BAD＝30°；
（3）作∠BAD和∠CAE的平分线AM、AN，在旋转过程中∠MAN的值是否发生变化？若不变，请求出这个定值；若变化，请求出变化范围．

18．（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．求证：CE＝CF；
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD．
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图3，在四边形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE=10, 求四边形ABCD的面积．

19．阅读下面材料：
小伟遇到这样一个问题：如图1，在△ABC（其中∠BAC是一个可以变化的角）中，AB=2，AC=4，以BC为边在BC的下方作等边△PBC，求AP的最大值．
小伟是这样思考的：利用变换和等边三角形将边的位置重新组合．他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC，连接A′A，当点A落在A′C上时，此题可解（如图2）．
请你回答：AP的最大值是　 　．
参考小伟同学思考问题的方法，解决下列问题：
如图3，等腰Rt△ABC．边AB=4，P为△ABC内部一点，则AP+BP+CP的最小值是　 　．（结果可以不化简）