第六章一次函数复习课件

这是一份第六章一次函数复习课件，共35页。

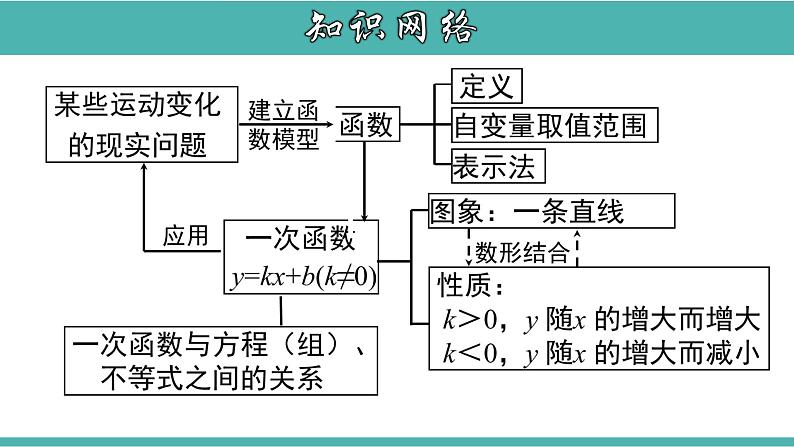
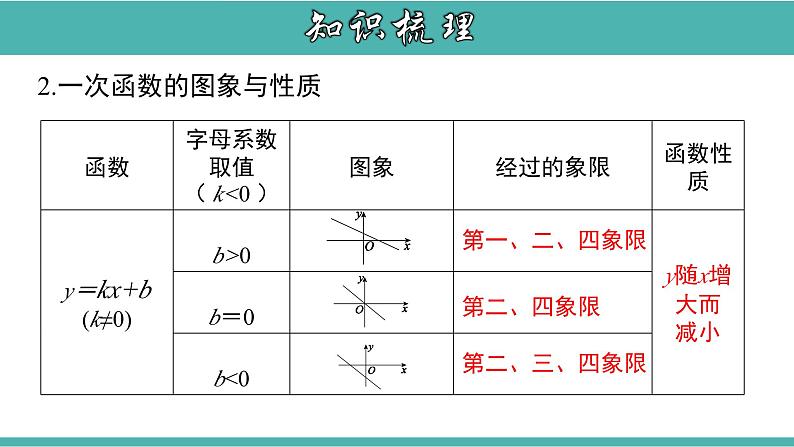
一次函数章节复习知识网络知识梳理1. 常量与变量 叫变量， 叫常量.数值发生变化的量数值始终不变的量 在一个变化过程中，如果有两个变量x与y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数.一、函数2.函数定义：知识梳理 3.函数的图象： 对于一个函数，如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象.列表法解析式法图象法5.函数的三种表示方法：4.描点法画图象的步骤：列表、描点、连线知识梳理0kx二、一次函数1.一次函数与正比例函数的概念知识梳理第一、三象限 第一、二、三象限 第一、三、四象限 2.一次函数的图象与性质知识梳理2.一次函数的图象与性质第一、二、四象限 第二、四象限 第二、三、四象限 知识梳理求一次函数解析式的一般步骤：（1）先设出函数解析式；（2）根据条件列关于待定系数的方程（组）；（3）解方程（组）求出解析式中未知的系数；（4）把求出的系数代入设的解析式，从而具体写出这个解析式.这种求解析式的方法叫待定系数法.3.用待定系数法求一次函数的解析式(1)一次函数与一元一次方程4.一次函数与方程、不等式求一元一次方程 kx+b=0(k≠0)的解求直线y= kx+b与 x 轴交点的横坐标。 求一次函数y= kx+b中y=0时x的值。知识梳理(2)一次函数与一元一次不等式求kx+b＞0(或<0)(k≠0)的解集求一次函数y=kx+b的值大于(或小于)0时，自变量x的取值范围确定直线y=kx+b在x轴上方(或下方)时对应x轴的哪一部分知识梳理 一般地，任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数，且k≠0)的形式，所以每个二元一次方程都对应一个一次函数，也对应一条直线．(3)一次函数与二元一次方程组方程组的解 对应两条直线交点的坐标.考点一 函数的有关概念及图象【例1】 王大爷饭后出去散步，从家中走20分钟到离家900米的公园，与朋友聊天10分钟后，用15分钟返回家中．下面图形表示王大爷离家时间x（分）与离家距离y（米）之间的关系是（ ）ABCDD【点睛】利用函数的图象解决实际问题，正确理解函数图象横纵坐标表示的意义，理解问题的过程，能够通过图象得到函数问题的相应解决．考点解析针对练习1.求下列函数的自变量的取值范围.    2.星期天下午，小强和小明相约在某公交车站一起乘车回学校，小强从家出发先步行到车站，等小明到了后两人一起乘公共汽车回到学校．图中折线表示小强离开家的路程y（千米）和所用的时间x（分）之间的函数关系．下列说法错误的是（ ）A．小强从家到公共汽车站步行了2千米B．小强在公共汽车站等小明用了10分钟C．公交车的平均速度是34千米/时D．小强乘公交车用了30分钟C针对练习考点二 一次函数的图象与性质【例2】已知函数y=（2m+1）x+m﹣3；(1)若该函数是正比例函数，求m的值；(2)若函数的图象平行直线y=3x﹣3，求m的值；(3)若这个函数是一次函数，且y随着x的增大而减小，求m的取值范围；(4)若这个函数图象过点（1，4），求这个函数的解析式.【分析】(1)由函数是正比例函数得m-3=0且2m+1≠0；(2)由两直线平行得2m+1=3；(3)一次函数中y随着x的增大而减小，即2m+1＜0；(4)代入该点坐标即可求解.考点解析1、A，B两点在一次函数图象上的位置如图所示，两点的坐标分别为A（x+a,y+b）,B（x,y）,下列结论正确的是（ ）yxoABA. a>0B. a<0C. b=0D. ab<0由图象可知： x+a< x y+b< y ∴a< 0, b< 0针对练习2..当k>0时，正比例函数y=kx的大致图象是 （ ）A.B.C.D.②.k>0图象经过一、三象限.①.图象经过原点.针对练习3、一次函数y=6x+1的图象不经过（ ）A.第一象限B.第二象限C.第三象限D.第四象限①.k=6>0图象经过一、三象限.②.b=1图象交在y轴的正半轴.针对练习4、已知一次函数y=（2m+1）x - m -1 的图象不经过第三象限，则m的取值范围是_________.针对练习考点三 一次函数的“图象共存”问题【例3】直线y1=kx+b和y2=bx+k在同一平面直角坐标系内的大致图象为（　） A. B. C. D.考点解析直线y1=kx+b和y2=bx+k在同一平面直角坐标系内的大致图象为（ 　 ） A. B. C. D.针对练习考点四 待定系数法求一次函数解析式【例4】一次函数的图象经过点A(-2，-3)，B(1,3)两点，求这个一次函数的表达式.考点解析1、已知A(1，3) 、B(－2，0) 、C(－4，m)三点在同一条直线上，求C点的坐标.针对练习2、已知一次函数的图象经过点A（2，1），且与直线y=-2x-3平行，求这个一次函数的表达式．针对练习3、已知一次函数y=-x+b与两条坐标轴围成三角形的面积是4，试求一次函数的解析式，并求出原点到这条直线的距离针对练习考点五 一次函数的平移规律（上、下平移）【例5】1.若将直线y=kx（k≠0）的图象向上平移3个单位长度后经过点（2，7），则平移后直线的解析式为（　　） A.y=2x+3 B.y=5x+3 C.y=5x-3 D.y=2x-32.直线y＝-2x＋1向____平移_____个单位长度所得直线的解析式为y＝-2x－4.考点解析考点六 一次函数与方程、不等式【例6】 如图，一次函数y1=x+b与一次函数y2=kx+4的图象交于点P（1，3），则关于x的不等式x+b＞kx+4的解集是（ ）yxOy1=x+by2=kx+4PA．x＞﹣2 B．x＞0 C．x＞1 D．x＜113【分析】观察图象，两图象交点为P(1，3),当x＞1时，y1在y2上方，据此解题即可.考点解析1.方程x+2=0的解就是函数y=x+2的图象与（ ）A.x轴交点的横坐标 B.y轴交点的横坐标C.y轴交点的纵坐标 D.以上都不对2.两个一次函数y=-x+5和y=-2x+8的图象的交点坐标是 _________.3.一次函数y=kx+b(k，b为常数，k≠0)的图象如图所示，根据图象信息可求得关于x的方程kx+b=0的解为________.针对练习 针对练习考点七 一次函数的实际应用(1)问符合题意的搭配方案有几种？请你帮助设计出来；(2)若搭配一个 A 种造型的成本是 800 元，搭配一个 B 种造型的成本是960元，试说明(1)中哪种方案成本最低？最低成本是多少元？【例7】为美化深圳市景，园林部门决定利用现有的 3490 盆甲种花卉和 2950 盆乙种花卉搭配 A、B 两种园艺造型共 50 个摆放在迎宾大道两侧，已知搭配一个 A 种造型需甲种花卉 80 盆，乙种花卉 40 盆，搭配一个 B 种造型需甲种花卉 50 盆，乙种花卉 90 盆．考点解析解：设搭配 A 种造型 x 个，则 B 种造型为(50－x)个，依题意，得 ∴31≤x≤33.∵x 是整数，x 可取 31,32,33，∴可设计三种搭配方案：①A 种园艺造型 31 个，B 种园艺造型 19 个；②A 种园艺造型 32 个，B 种园艺造型 18 个；③A 种园艺造型 33 个，B 种园艺造型 17 个． 解得考点解析方案①需成本：31×800＋19×960＝43040(元)；方案②需成本：32×800＋18×960＝42880(元)；方案③需成本：33×800＋17×960＝42720(元)．（2）方法一：方法二：成本为y＝800x＋960(50－x)＝－160x＋48000(31≤x≤33)．根据一次函数的性质，y 随 x 的增大而减小，故当 x＝33 时，y 取得最小值为33×800＋17×960＝42720(元)．即最低成本是 42720 元．考点解析针对练习1.某家电集团生产某种型号的新家电，前期投资200万元，每生产1台这种新家电，后期还需其他投资0.3万元，已知每台新家电可实现产值0.5万元.（1）分别求出总投资额y1（万元）和总利润y2（万元）关于新家电的总产量x（台）的函数解析式；（2）当新家电的总产量为900台时，该公司的盈亏情况如何？（3）请你利用（1）中y2和x的函数解析式，分析该公司的盈亏情况.考点八 一次函数与几何综合应用 考点解析谢谢观看！