
初中数学人教版八年级上册第十二章 全等三角形12.2 三角形全等的判定第4课时教学设计
展开12.2 第4课时 “斜边、直角边”
一、教学目标
1.理解并掌握三角形全等的判定方法——“斜边、直角边”.
2.经历探究“斜边、直角边”判定方法的过程,能运用“斜边、直角边”判定方法解决有关问题.
二、教学重难点
重点:理解并掌握三角形全等的判定方法——“斜边、直角边”.
难点:经历探究“斜边、直角边”判定方法的过程,能运用“斜边、直角边”判定方法解决有关问题.
三、教学过程
(一)情境导入
舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.
(1)你能帮他想个办法吗?
(2)如果他只带了一个卷尺,能完成这个任务吗?
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”,你相信他的结论吗?

(二)合作探究
探究点一:应用“斜边、直角边”判定三角形全等
例1:如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:Rt△ABF≌Rt△DCE.
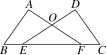
解析:由题意可得△ABF与△DCE都为直角三角形,由BE=CF可得BF=CE,然后运用“HL”即可判定Rt△ABF与Rt△DCE全等.
证明:∵BE=CF,∴BE+EF=CF+EF,即BF=CE.∵∠A=∠D=90°,∴△ABF与△DCE都为直角三角形.在Rt△ABF和Rt△DCE中,∵
∴Rt△ABF≌Rt△DCE(HL).
方法总结:利用“HL”判定三角形全等,首先要判定这两个三角形是直角三角形,然后找出对应的斜边和直角边相等即可.
探究点二:“斜边、直角边”判定三角形全等的运用
【类型一】 利用“HL”判定线段相等
例2: 如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.求证:BC=BE.
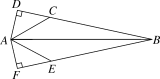
解析:根据“HL”证Rt△ADC≌Rt△AFE,得CD=EF,再根据“HL”证Rt△ABD≌Rt△ABF,得BD=BF,最后证明BC=BE.
证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,∴Rt△ADC≌Rt△AFE(HL).∴CD=EF.∵AD=AF,AB=AB,∴Rt△ABD≌Rt△ABF(HL).∴BD=BF.∴BD-CD=BF-EF.即BC=BE.
方法总结:证明线段相等可通过证明三角形全等解决,作为“HL”公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
【类型二】 利用“HL”判定角相等或线段平行
例3:![]() 如图,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2.
如图,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2.
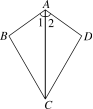
解析:要证角相等,可先证明全等.即证Rt△ABC≌Rt△ADC,进而得出角相等.
证明:∵AB⊥BC,AD⊥DC,∴∠B=∠D=90°,∴△ABC与△ACD为直角三角形.在Rt△ABC和Rt△ADC中,∵∴Rt△ABC≌Rt△ADC(HL),∴∠1=∠2.
方法总结:证明角相等可通过证明三角形全等解决.
【类型三】 利用“HL”解决动点问题
例4: 如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等?
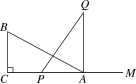
解析:本题要分情况讨论:(1)Rt△APQ≌Rt△CBA,此时AP=BC=5cm,可据此求出P点的位置.(2)Rt△QAP≌Rt△BCA,此时AP=AC,P、C重合.
解:根据三角形全等的判定方法HL可知:(1)当P运动到AP=BC时,∵∠C=∠QAP=90°.在Rt△ABC与Rt△QPA中,∵∴Rt△ABC≌Rt△QPA(HL),∴AP=BC=5cm;(2)当P运动到与C点重合时,AP=AC.在Rt△ABC与Rt△QPA中,∵∴Rt△QAP≌Rt△BCA(HL),∴AP=AC=10cm,∴当AP=5cm或10cm时,△ABC才能和△APQ全等.
方法总结:判定三角形全等的关键是找对应边和对应角,由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.
【类型四】 综合运用全等三角形的判定方法判定直角三角形全等
例5: 如图,CD⊥AB于D点,BE⊥AC于E点,BE,CD交于O点,且AO平分∠BAC.求证:OB=OC.
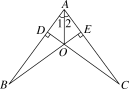
解析:已知BE⊥AC,CD⊥AB可推出∠ADC=∠BDC=∠AEB=∠CEB=90°,由AO平分∠BAC可知∠1=∠2,然后根据AAS证得△AOD≌△AOE,根据ASA证得△BOD≌△COE,即可证得OB=OC.
证明:∵BE⊥AC,CD⊥AB,∴∠ADC=∠BDC=∠AEB=∠CEB=90°.∵AO平分∠BAC,∴∠1=∠2.在△AOD和△AOE中,∵
∴△AOD≌△AOE(AAS).∴OD=OE.在△BOD和△COE中,∵∴△BOD≌△COE(ASA).∴OB=OC.
方法总结:判定直角三角形全等的方法除“HL”外,还有:SSS、SAS、ASA、AAS.
四、板书设计
“斜边、直角边”
1.斜边、直角边:斜边和一条直角边分别相等的两个直角三角形全等.简记为“斜边、直角边”或“HL”.
2.方法归纳:
(1)证明两个直角三角形全等的常用方法是“HL”,除此之外,还可以选用“SAS”“ASA”“AAS”以及“SSS”.
(2)寻找未知的等边或等角时,常考虑转移到其他三角形中,利用三角形全等来进行证明.
五、教学反思
本节课的教学主要通过分组讨论、操作探究以及合作交流等方式来进行.在探究直角三角形全等的判定方法——“斜边、直角边”时,要让学生进行合作交流.在寻找未知的等边或等角时,常考虑将其转移到其他三角形中,利用三角形全等来进行证明.此外,还要注重通过适量的练习巩固所学的新知识.
数学八年级上册12.2 三角形全等的判定第4课时教案设计: 这是一份数学八年级上册12.2 三角形全等的判定第4课时教案设计,共4页。教案主要包含了教学重点,教学难点,教学说明等内容,欢迎下载使用。
人教版八年级上册12.2 三角形全等的判定第4课时教学设计及反思: 这是一份人教版八年级上册12.2 三角形全等的判定第4课时教学设计及反思,共4页。
人教版八年级上册第十二章 全等三角形12.2 三角形全等的判定第4课时教学设计及反思: 这是一份人教版八年级上册第十二章 全等三角形12.2 三角形全等的判定第4课时教学设计及反思,共8页。教案主要包含了知识链接,新知预习,我的疑惑等内容,欢迎下载使用。













