





















- 人教版初中数学九年级上册 24.1.2 《 垂直于弦的直径》 课件+教案+导学案+分层作业(含教师学生版和教学反思) 课件 8 次下载
- 人教版初中数学九年级上册 24.1.3 《 弧、弦、圆心角》 课件+教案+导学案+分层作业(含教师学生版和教学反思) 课件 8 次下载
- 人教版初中数学九年级上册 24.1.4 《 圆周角(第二课时)》 课件+教案+导学案+分层作业(含教师学生版和教学反思) 课件 7 次下载
- 人教版初中数学九年级上册 24.2.1 《 点和圆的位置关系》 课件+教案+导学案+分层作业(含教师学生版和教学反思) 课件 8 次下载
- 人教版初中数学九年级上册 24.2.2 《 直线与圆的位置关系(第一课时》 课件+教案+导学案+分层作业(含教师学生版和教学反思) 课件 7 次下载
初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.4 圆周角优质教学作业课件ppt
展开![]() 24.1.4 圆周角(第一课时)
24.1.4 圆周角(第一课时)
学习目标:
1)理解圆周角的定义。
2)掌握圆周角定理。
3)运用圆周角定理进行简单的计算和证明。
学习重点: 理解并掌握圆周角定理。
学习难点: 运用圆周角定理进行简单的计算和证明。
学习过程
1)课前回顾
圆心角的定义:__________叫做圆心角。
圆心角的判断方法:观察顶点是否在__________。
 2)课堂探究
2)课堂探究
一、圆周角概念理解
【观察与思考】将圆心角顶点上移,直至与⊙O相交于点C?观察得到的∠ACB有什么特征?
特征:__________在圆上,__________都与圆相交。
 圆周角的概念:__________在圆上,____________________叫做圆周角。
圆周角的概念:__________在圆上,____________________叫做圆周角。
【问题1】你能指出右图中的圆周角吗?
【问题2】判断下列各图中的哪个角是圆周角。

二、探索圆周角定理
【探索与思考】在纸上画出一个圆,并截取任意一条圆弧画出其所对的圆心角和圆周角,测量它们的度数,你发现了什么?
发现:
【证明】下面我们分以下三种情况验证上述猜想:
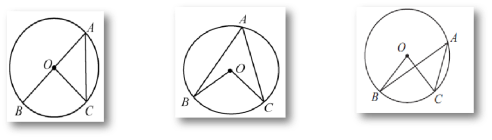
圆心在圆周角一边上 圆心在圆周角内部 圆心在圆周角外部
【情况一】圆心在圆周角一边上
【情况二】圆心在圆周角内部
【情况三】圆心在圆周角外部
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的__________。
【练一练】
1.如图,△ABC内接于圆,弦BD交AC于点P,连接AD.下列角中,![]() 所对圆周角的是( )
所对圆周角的是( )

A.∠APB B.∠ABD C.∠ACB D.∠BAC
2.下列图形中的角是圆周角的是( )
A. B.
B. C.
C. D.
D.
3.如图,其中圆周角有( )
A.1个 B.2个 C.3个 D.4个
4.如图,![]() 是
是![]() 的直径,
的直径,![]() 为圆内一点,则下列说法中正确的是( )
为圆内一点,则下列说法中正确的是( )

A.![]() 是
是![]() 的弦 B.
的弦 B.![]() 是圆心角
是圆心角
C.![]() 是圆周角 D.
是圆周角 D.![]()
5.如图,点A,B,C,D,E都在⊙O上,∠BAC=15°,∠BOD=70°,则∠CED的度数是( )

A.15° B.20° C.25° D.55°
6.如图,点![]() 都在⊙O上,
都在⊙O上,![]() ,则∠DOE=( )
,则∠DOE=( )
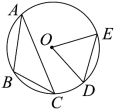
A.24° B.42° C.48° D.72°
7.如图,已知AB为⊙O的弦,C为![]() 的中点,点D在优弧
的中点,点D在优弧![]() 上一点,连接AD下列式子一定正确的是( )
上一点,连接AD下列式子一定正确的是( )
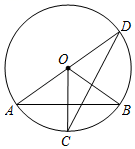
A.∠ADC=∠B B.∠ADC+2∠B=90°
C.2∠ADC+∠B=90° D.∠B=30°
8.如图,AB为⊙O的直径,半径OA的垂直平分线交⊙O于点C,D,P为优弧ABC上一点,则∠APC=( )
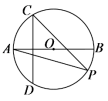
A.20° B.30° C.35° D.40°
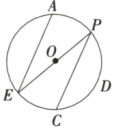
9.如图,若![]() 的度数为105°,则∠BAE=________.
的度数为105°,则∠BAE=________.

10.如图,![]() 是半圆
是半圆![]() 的直径,且
的直径,且![]() ,在半圆
,在半圆![]() 上取一点
上取一点![]() ,使得
,使得![]() ,则
,则![]() ________
________![]() .
.
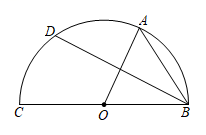
11.如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为 ___.

12.如图,如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
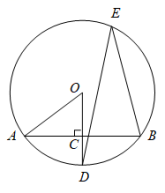
(1)若∠AOD=62°,求![]() 的度数;
的度数;
(2)若OC=6,OA=10,求![]() 的长.
的长.
13.如图,四边形ABCD是⊙O的内接四边形,![]() ,∠ABD=33°,∠ACB=44°.
,∠ABD=33°,∠ACB=44°.
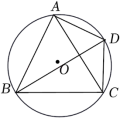
(1)求∠BAC的度数.
(2)求∠BAD的度数.
【学后反思】通过本节课的学习你,你收获了什么?
初中第二十四章 圆24.1 圆的有关性质24.1.4 圆周角课前预习课件ppt: 这是一份初中第二十四章 圆24.1 圆的有关性质24.1.4 圆周角课前预习课件ppt,共18页。
初中人教版24.1.4 圆周角说课ppt课件: 这是一份初中人教版24.1.4 圆周角说课ppt课件,共18页。PPT课件主要包含了学习目标,圆周角定理的推导,针对训练等内容,欢迎下载使用。
人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.4 圆周角教案配套ppt课件: 这是一份人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.4 圆周角教案配套ppt课件,共24页。PPT课件主要包含了回顾旧知,如何证明,随堂练习,课堂小结等内容,欢迎下载使用。














