易错点04 一元二次不等式及一元二次方程-备战2024年高考数学考试易错题（新高考专用）

这是一份易错点04 一元二次不等式及一元二次方程-备战2024年高考数学考试易错题（新高考专用），文件包含易错点04一元二次不等式及一元二次方程-备战2024年高考数学易错题新高考专用解析版docx、易错点04一元二次不等式及一元二次方程-备战2024年高考数学易错题新高考专用原卷版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。

解一元二次不等式忽视两根的大小关系
一元二次不等式恒成立忽视区间的开闭
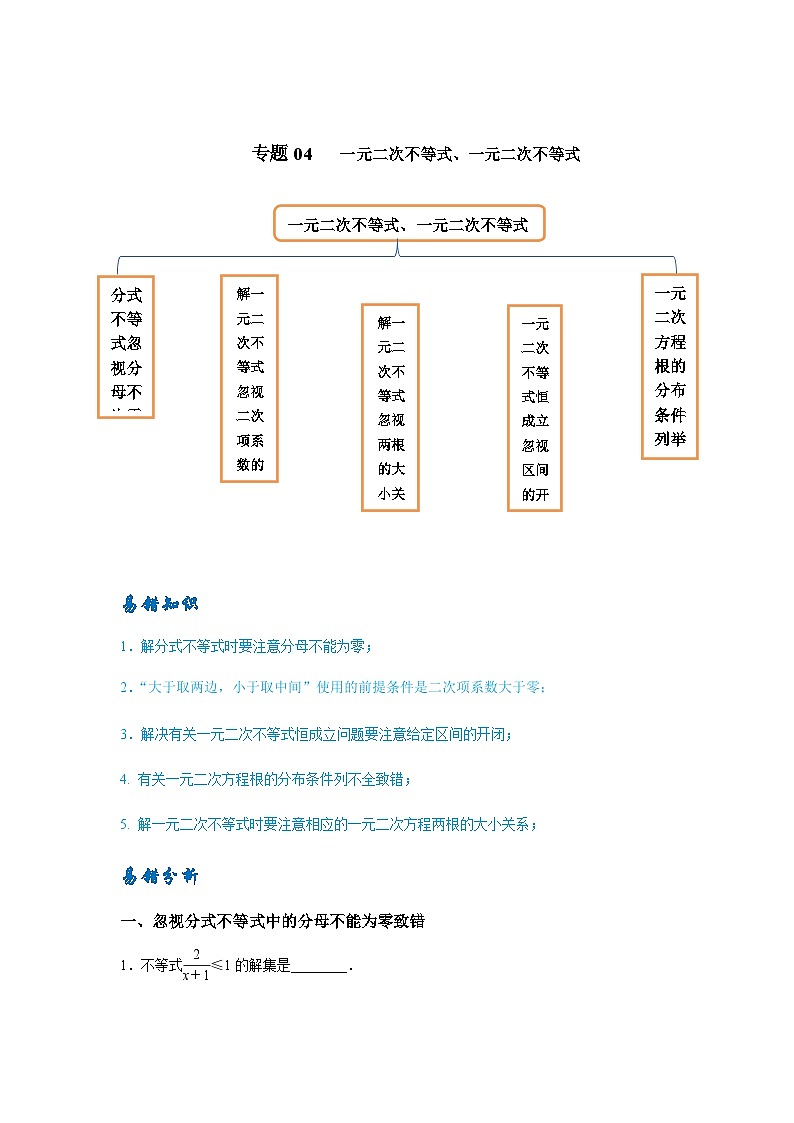
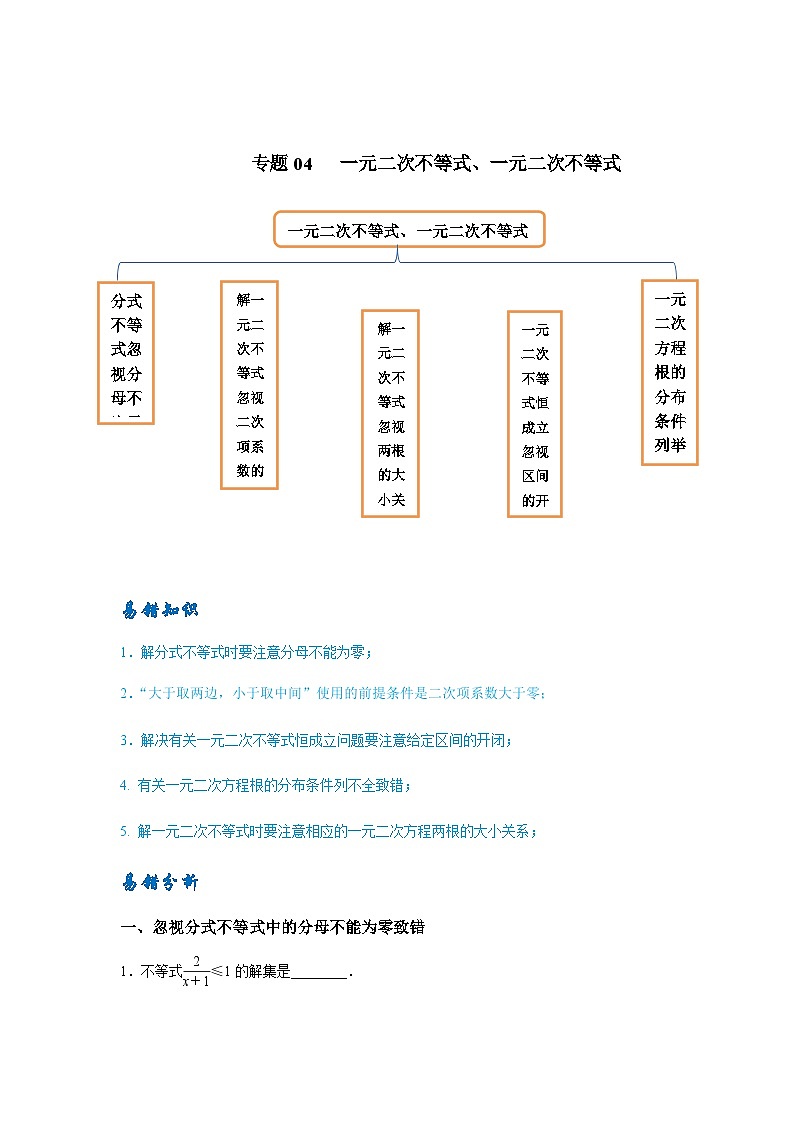
易错知识
1．解分式不等式时要注意分母不能为零；
2．“大于取两边，小于取中间”使用的前提条件是二次项系数大于零；
3．解决有关一元二次不等式恒成立问题要注意给定区间的开闭；
4. 有关一元二次方程根的分布条件列不全致错；
5. 解一元二次不等式时要注意相应的一元二次方程两根的大小关系；
易错分析
一、忽视分式不等式中的分母不能为零致错
1．不等式eq \f(2,x＋1)≤1的解集是________．
【错解】由eq \f(2,x＋1)≤1得eq \f(2,x＋1)－1≤0，得eq \f(2－x－1,x＋1)≤0，得eq \f(x－1,x＋1)≥0，得(x－1)(x＋1)≥0，得x≤－1或x≥1，所以原不等式的解集为{x|xx≤－1或x≥1}．
【错因】因为x＋1为分母，所以x＋1不等于零。
【正解】由eq \f(2,x＋1)≤1得eq \f(2,x＋1)－1≤0，得eq \f(2－x－1,x＋1)≤0，得eq \f(x－1,x＋1)≥0，得x－1＝0或(x－1)(x＋1)>0，得x＝1或x1，得x