易错点05 函数概念及其性质-备战2024年高考数学考试易错题（新高考专用）

这是一份易错点05 函数概念及其性质-备战2024年高考数学考试易错题（新高考专用），文件包含易错点05函数概念及其性质-备战2024年高考数学易错题新高考专用解析版docx、易错点05函数概念及其性质-备战2024年高考数学易错题新高考专用原卷版docx等2份试卷配套教学资源，其中试卷共20页， 欢迎下载使用。
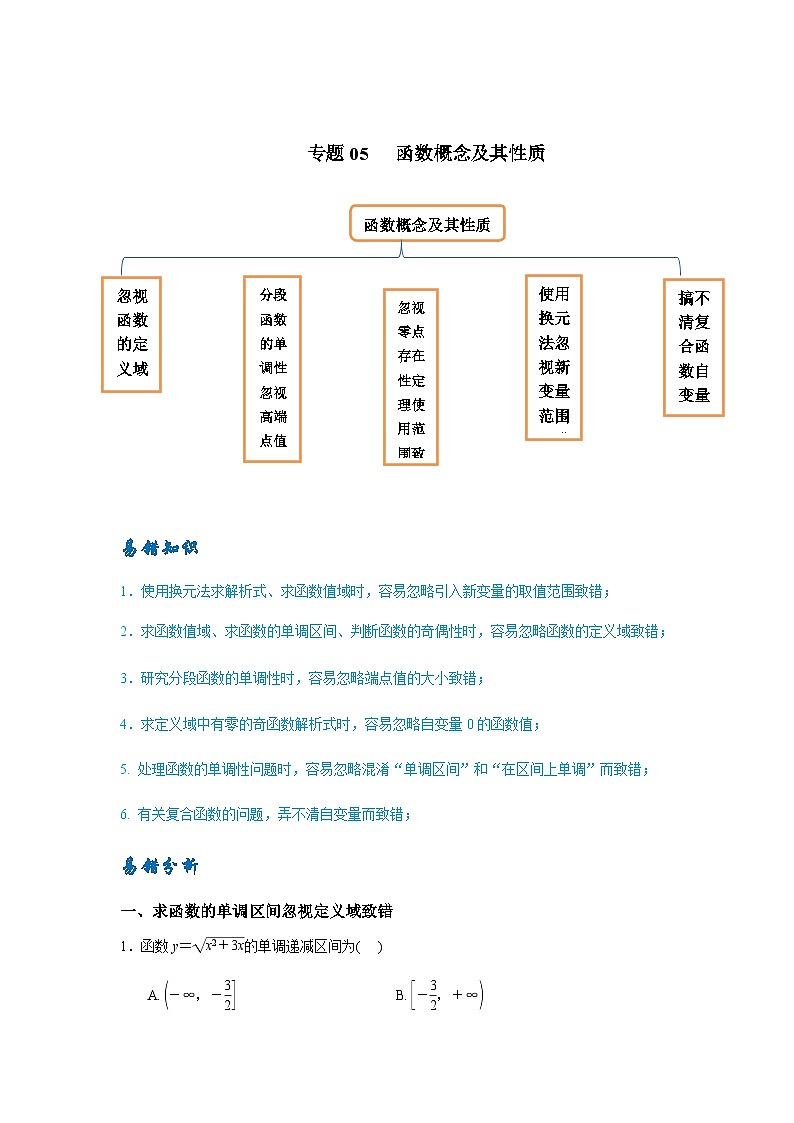
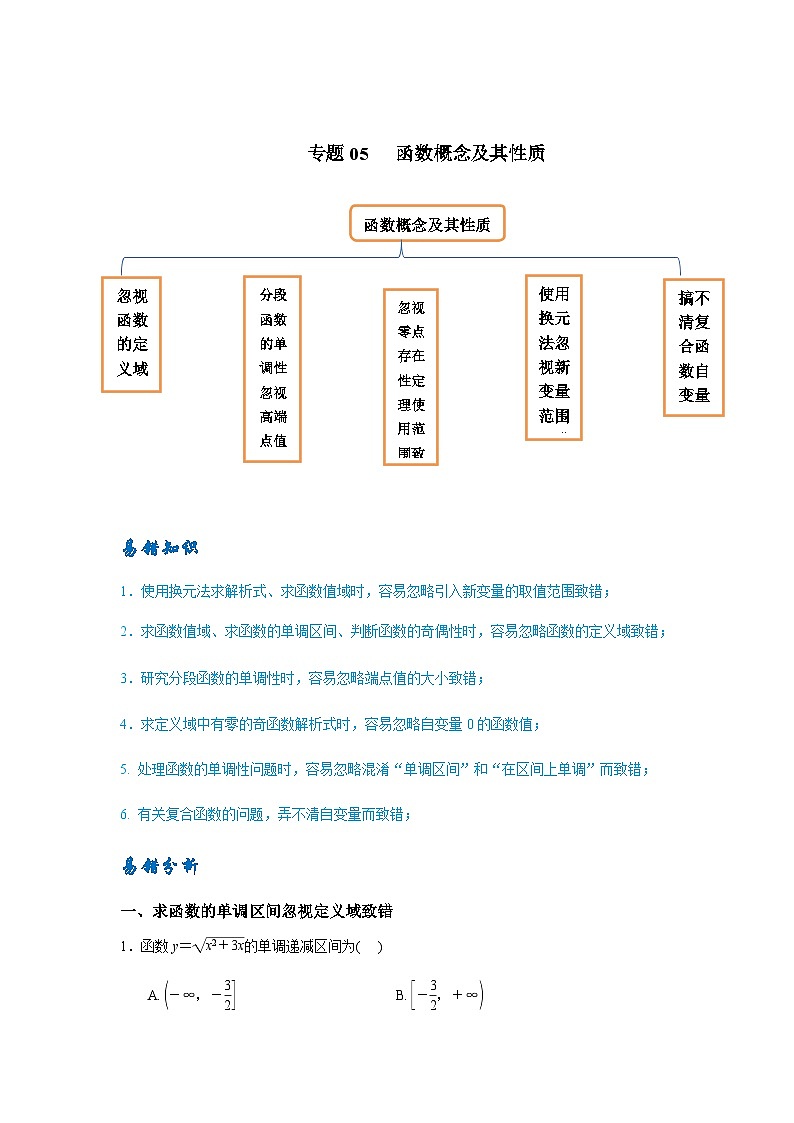
函数概念及其性质
忽视函数的定义域致错
分段函数的单调性忽视高端点值致错
使用换元法忽视新变量范围致错
搞不清复合函数自变量致错
忽视零点存在性定理使用范围致错
易错知识
1．使用换元法求解析式、求函数值域时，容易忽略引入新变量的取值范围致错；
2．求函数值域、求函数的单调区间、判断函数的奇偶性时，容易忽略函数的定义域致错；
3．研究分段函数的单调性时，容易忽略端点值的大小致错；
4．求定义域中有零的奇函数解析式时，容易忽略自变量0的函数值；
5. 处理函数的单调性问题时，容易忽略混淆“单调区间”和“在区间上单调”而致错；
6. 有关复合函数的问题，弄不清自变量而致错；
易错分析
一、求函数的单调区间忽视定义域致错
1．函数y＝eq \r(x2＋3x)的单调递减区间为( )
A.eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(3,2))) B.eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(3,2)，＋∞))
C．[0，＋∞) D．(－∞，－3]
【错解】选A 令t＝x2＋3x，y＝eq \r(x2＋3x)是由y＝eq \r(t)与t＝x2＋3x复合而成，又外层函数y＝eq \r(t)在[0，＋∞)上单调递增，内层函数t＝x2＋3x在eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(3,2))) 上单调递减，在eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(3,2)，＋∞))上单调递增，根据复合函数同增异减的原则可知，函数y＝eq \r(x2＋3x)的单调递减区间为eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(3,2))) ．
【错因】没有考虑函数y＝eq \r(x2＋3x)的定义域，
【正解】选D 由题意，x2＋3x≥0，可得x≤－3或x≥0，函数y＝eq \r(x2＋3x)的定义域为
(－∞，－3]∪[0，＋∞)．令t＝x2＋3x，则外层函数y＝eq \r(t)在[0，＋∞)上单调递增，内层函数
t＝x2＋3x在(－∞，－3]上单调递减，在[0，＋∞)上单调递增，所以，函数y＝eq \r(x2＋3x)的单调递减区间为(－∞，－3]．
二、判断函数的奇偶性忽视定义域致错
2．判断函数f(x)＝eq \r(\f(1－x,1＋x))的奇偶性：
【错解】
，所以函数f(x)＝eq \r(\f(1－x,1＋x))为偶函数。
【错因】没有考虑函数f(x)＝eq \r(\f(1－x,1＋x))的定义域，
【正解】因为f(x)有意义，则满足eq \f(1－x,1＋x)≥0，所以－1