七年级数学下册第2章整式的乘法2.2乘法公式复习练习题（附答案湘教版七下）

这是一份七年级数学下册第2章整式的乘法2.2乘法公式复习练习题（附答案湘教版七下），共4页。
第2章　整式的乘法   2.2　乘法公式1．下列各式中能用平方差公式的是(　　)A．(x＋y)(y＋x)                B．(x＋y)(y－x)C．(x＋y)(－y－x)              D．(－x＋y)(y－x)2．下列各式计算正确的是(　　)A．(a＋b)2＝a2＋b2              B．(－ab2)3＝a3b6C．2a2＋3a2＝5a4                D．(b＋2a)(2a－b)＝4a2－b23．若xy＝12，(x－3y)2＝25，则(x＋3y)2的值为(　　)A．196    B．169     C.156     D．1444．若三角形的底边长为2a＋1，底边上的高为2a－1，则此三角形的面积为(　　)A．4a2－1     B．4a2－4a＋1   C．4a2＋4a＋1    D．2a2－　5．已知(－3a＋m)(4b＋n)＝16b2－9a2，则m、n的值分别为(　　)A．m＝－4b，n＝3a         B．m＝4b，n＝－3aC．m＝4b，n＝3a           D．m＝3a，n＝4b6．如果x2＋mx＋1恰好是一个整式的平方，那么常数m的值是(　　)A．1    B．2    C.±1    D．±27．将图甲中阴影部分的小长方形变换到图乙位置，根据两个图形的面积关系可以得到一个关于a、b的恒等式为(　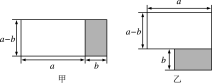　)A．(a－b)2＝a2－2ab＋b2      B．(a＋b)2＝a2＋2ab＋b2C．(a＋b)(a－b)＝a2－b2      D．a(a－b)＝a2－ab8．一个边长为acm的正方形，若将其边长增加6cm，则新的正方形的面积增加(　　)A．36cm2     B．12acm2   C．(36＋12a)cm2    D．以上都不对9．一个正整数若能表示为两个正整数的平方差，则称这个正整数为“创新数”，比较41＝212－202，故41是一个“创新数”．下列各数中，不是“创新数”的是(　　)A．16    B．19    C.27    D．3010．若(5x＋6y)(ax－by)＝36y2－25x2，则a、b的值为(　　)A．a＝－5，b＝－6  B．a＝5，b＝6C．a＝5，b＝－6  D．a＝－5，b＝611．计算：(x＋2)2－(x－1)(x＋1)＝         .12．已知x2－y2＝4，则(x＋y)3(x－y)3＝       .13．一个长方形的长、宽分别为a、b，周长为14，面积为10，则a2＋b2＝       .14．将边长分别为(a＋b)和(a－b)的两个正方形摆放成如图所示的位置，则阴影部分的面积化简后的结果是         .15．请看杨辉三角(1)，并观察下列等式(2)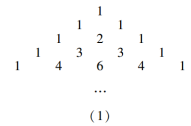：(a＋b)1＝a＋b(a＋b)2＝a2＋2ab＋b2(a＋b)3＝a3＋3a2b＋3ab2＋b3(a＋b)4＝a4＋4a3b＋6a2b2＋4ab3＋b4(2)根据前面各式的规律，则(a＋b)5＝                                  .16．现定义运算“△”，对于任意有理数a、b，都有a△b＝a2－ab＋b，例如：3△5＝32－3×5＋5＝－1，由此算出(x－1)△(2＋x)＝           .17．计算下列各题：(1)4(a－b)2－(2a＋b)(－b＋2a)； (2)(3x－2y)(9x2＋4y2)(－2y－3x)； (3)(x＋2y－z)(x－2y－z)－(x＋y－z)2. 18. 先化简，再求值：(a－2b)(a＋2b)－(a－2b)2＋8b2，其中a＝－2，b＝.  19．已知a＋b＝6，ab＝2.(1)求a2＋b2的值；(2)求(a－b)2的值．     20．在化简求(a＋3b)2＋(2a＋3b)(2a－3b)＋a(5a－6b)的值时，亮亮把a的值看错后代入得结果为10，而小莉代入正确的a的值得到正确的结果也是10，经探究后，发现所求代数式的值与b无关，则他们俩代入的a的值的和是多少？     21．在日历上，我们可以发现其中某些数满足一定的规律，如图是2014年12月份的日历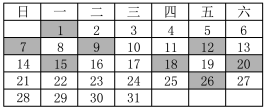． 如图所选择的两组四个数，分别将每组数中相对的两数相乘，再相减，例如：7×9－1×15＝        ，18×20－12×26＝        ，不难发现，结果都是        ．(1)请将上面三个空补充完整；(2)我们发现选择其他类似的部分规律也相同，请你利用整式的运算对以上的规律加以证明．              答案：1-10   BDBDC   DCCDA11. 4x＋512. 6413. 2914. 4ab15. a5＋5a4b＋10a3b2＋10a2b3＋5ab4＋b5 16. －2x＋5 17. (1) 解：原式＝4(a2－2ab＋b2)－(4a2－b2)＝4a2－8ab＋4b2－4a2＋4b2＝－8ab＋8b2；(2) 解：原式＝(－2y＋3x)(－2y－3x)(9x2＋4y2)＝(4y2－9x2)(9x2＋4y2)＝16y4－81x4；(3) 解：原式＝[(x－z)＋2y][(x－z)－2y]－[(x－z)＋y]2＝(x－z)2－4y2－(x－z)2－2(x－z)y－y2＝－5y2－2xy＋2yz.18. 解：原式＝a2－4b2－a2＋4ab－4b2＋8b2＝4ab，当a＝－2，b＝时，4ab＝4×(－2)×＝－4.19. 解：(1)∵a＋b＝6，∴(a＋b)2＝36，即a2＋b2＋2ab＝36，∵ab＝2，∴a2＋b2＝36－4＝32；(2)(a－b)2＝a2＋b2－2ab＝32－4＝28.20. 解：原式＝a2＋6ab＋9b2＋4a2－9b2＋5a2－6ab＝10a2，因为代入a的值的结果是10，所以10a2＝10，a2＝1，a＝±1，即：他们代入的a的值的和为0.21. 解：(1)48,48,48；　(2)设四个数围起来的中间的数为x，则这四个数依次为x－7，x－1，x＋1，x＋7，则(x－1)(x＋1)－(x－7)(x＋7)＝48.