初中数学湘教版七年级下册5.3 图形变换的简单应用精品课后测评

5.3　图形变换的简单应用

1.由仅经过一次平移、旋转或轴对称变换,不能得到的图形是 (　　)

2.在如图所示的方格纸中,小树从位置A经过旋转、平移后到位置B,那么下列说法正确的是              (　　)

A.绕点A逆时针旋转90°,再向右平移7格

B.绕点A逆时针旋转45°,再向右平移7格

C.绕点A顺时针旋转90°,再向右平移7格

D.绕点A顺时针旋转45°,再向右平移7格

3.下列四个图形中,若以其中一部分作为基本图案,无论用旋转还是用平移都不能得到的图形是(　　)

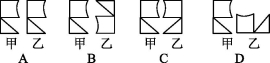
4.如图,经过平移或旋转不可能将甲图案变成乙图案的是 (　　)

5.下列图案中,可以由一个“基本图形”连续旋转45°得到的是 (　　)

6.如图,这个图形可以看成是以“基本图形”即原图形的四分之一经过变换形成的,但一定不能经过哪种变换得到              (　　)

A.轴对称和旋转                   B.轴对称

C.平移                           D.旋转

7.观察,请你说出它的“基本图案”是什么?这个图案又是怎样形成的呢?

8.一名同学想用正方形和圆设计一个图案,要求整个图案关于正方形的某条对角线所在的直线对称,那么中的各图案中不符合要求的是              (　　)

9.认真观察0①~④的四个图案,回答下列问题:

(1)请写出这四个图案都具有的两个共同特征;

(2)请你在图⑤中设计出你心中最美的图案,使它也具备你所写出的上述特征.

10.下面的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有              (　　)

1

A.4个     B.3个     C.2个     D.1个

11.2是4×4的正方形网格,其中已有3个小正方形被涂成了灰色,现在要从其余13个白色小方格中选出一个也涂成灰色,使灰色部分成为轴对称图形,这样的白色小方格有              (　　)

A.2个          B.3个              C.4个            D.5个

12.在如图所示的方格纸中,每个小方格都是边长为1个单位长度的小正方形,三角形①②③均为顶点都在格点上的三角形(每个小方格的顶点叫格点).

(1)在图(a)中,三角形②可由三角形①经过什么变换(选“平移”“旋转”或“轴对称”)得到?

(2)在图(a)中,三角形③可以由三角形②经过旋转变换得到,其旋转中心是哪一点(选“A”或“B”或“C”)?

(3)在图(b)中画出三角形①绕点A顺时针旋转90°后得到的三角形④.

13.小宁和婷婷在一起做拼图游戏,她们用“○○,△△,||”构思出了独特而有意义的图形,并根据图形用简洁的语言进行了表述(如图):

观察以上图案:

(1)它们可以通过一个“基本图案”经过怎样的平移而形成?

(2)在平移的过程中,“基本图案”的大小、形状、位置是否发生了变化?你能解释其中的道理吗?

参考答案

1.B　

2.B　

3.C　

4.C　

5.D　[解析] 四个选项中,均可由一个基本图形连续旋转得到,其旋转的度数依次是120°,72°,60°,45°.故选D.

6.C

7.解:它的基本图案是,经过平移可以得到原图案.(答案不唯一)

8.D　[解析] 选项D的对称轴是每组对边的垂直平分线.

9.解:(1)答案不唯一,如图特征1:都是轴对称图形;特征2:都可以通过旋转得到.

(2)答案不唯一,如图图所示.

10.A　[解析] 图形①可以看成是一个以正方形中心和相邻两个顶点形成的三角形,沿着大正方形的对角线所在的直线对折三次得到的,也可以看成是以正方形中心和相邻两个顶点形成的三角形,围绕正方形中心顺时针(或逆时针)依次旋转90°,180°,270°得到的;图形②可以看成是沿着大正方形对边中点所在的直线对折得到的,也可以看成是正方形三个顶点形成的三角形围绕正方形中心顺时针(或逆时针)旋转180°得到的;图形③可以看成是正方形三个顶点形成的三角形沿着大正方形的对角线所在的直线对折得到的,也可以看成是正方形三个顶点形成的三角形围绕正方形中心顺时针(或逆时针)旋转180°得到的;图形④可以看成是一个小正方形沿着大正方形对边的中点所在的直线对折三次得到的,也可以看成是小正方形围绕大正方形中心顺时针(或逆时针)依次旋转90°,180°,270°得到的.所以符合题目要求的图形有4个.故选A.

11.C　[解析] 如图图所示,有4个位置可使之成为轴对称图形.故选C.

12.解:(1)三角形①经过平移变换可以得到三角形②.

(2)旋转中心是点A.

(3)略.

13.解:(1)图①②③均可以看成前一个图形是后一个图形向前平移一定距离后得到的;图④中下面的图形可以看成是上面图形向下平移一段距离再向右平移一段距离后得到的.(答案不唯一)

(2)在平移的过程中,“基本图案”的大小、形状不发生变化,位置发生变化.由平移的定义可知,平移不改变图形的大小和形状,只改变图形的位置.