

北师大版七年级上册第二章 有理数及其运算2.3 绝对值教案设计
展开第二章 有理数及其运算
2. 3 绝对值
![]()
绝对值的概念能更深刻地理解相反数的概念,同时为以后有理数的运算打下了基础,因此绝对值的意义,以及求一个数的绝对值,是本节课的重点.绝对值对于学生而言是一个比较难接受,较难理解的概念,掌握不好,今后对绝对值的计算,会产生很大的影响,因此,本节课的难点是绝对值定义的得出、意义的理解及求一个负数的绝对值.绝对值沟通了有理数与以前学段学过的数之间的联系,从而为有理数的大小比较,有理数的运算打下了基础.本课意在让学生亲身经历将实际问题抽象成数学模型的过程,进而使学生获得对数学理解的同时,在思维能力、情感态度与价值观等方面得到进步和发展,并通过一系列探索性的问题及游戏,让学生在掌握新知的同时,体验成功的乐趣.
![]()
- 借助数轴理解绝对值的意义,能准确熟练地求一个有理数的绝对值,使学生知道绝对值是一个非负数,能更深刻地理解相反数的概念.
- 通过探索正数、负数及0的绝对值的过程,初步培养学生观察、分析、归纳和概括的思维能力,培养学生由抽象到具体再到抽象的思维能力.
- 情感态度与价值观:通过本课的学习向学生渗透数形结合思想和分类讨论的思想,让学生领略到数学的奥妙,从而激起他们的好奇心和求知欲望.通过课堂上生动活泼和愉快、轻松地学习,使学生感受到学习数学的快乐,从而增强他们的自信心.
![]()
【教学重点】
绝对值的意义以及求一个数的绝对值.
【教学难点】
绝对值定义的得出、意义的理解及求一个负数的绝对值.
![]()
情境教学法,启发引导法,讨论法.
![]()
一、 复习回顾
1. 相反数
3 与 -3 有什么相同点?![]() 与
与![]() , 5 与 -5 呢?你还能列举两个这样的数吗?与同伴进行交流.
, 5 与 -5 呢?你还能列举两个这样的数吗?与同伴进行交流.
如果两个数只有符号不同,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数. 特别地,0的相反数是0.
二、合作交流,探究新知

一个数 a 的绝对值就是数轴上表示数 a 的点与原点的距离.
一个数的绝对值就是在这个数的两旁各画一条竖线,如 +2 的绝对值等于 2,记作 |+2| = 2.
数 a 的绝对值记作 | a |.
如图,在数轴上表示-5的点与原点的距离是5,即-5的绝对值是5,记作|-5=5.
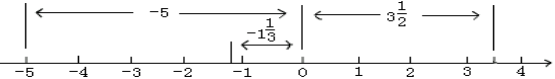
想一想:
互为相反数的两个数的绝对值有什么关系?
一对相反数虽然分别在原点两边, 但它们到原点的距离是相等的.

一个数的绝对值与这个数有什么关系?
绝对值的性质:正数绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.
三、应用新知
1. 绝对值是 10 的数有( )
| +15 | = | –4 | = | 0 | = | 4 | =
2. 判断:
(1)绝对值都是正数. ( )
(2)互为相反数的绝对值相等. ( )
3. 一个数的绝对值是它本身,那么这个数一定是__________.
四、巩固新知
1.(1)在数轴上表示下列各数,并比较它们的大小:
- 1.5 , - 3 , - 1 , - 5
(2) 求出(1)中各数的绝对值,并比较它们的大小
(3)你发现了什么?
2. 比较下列每组数的大小
(1) -1 和 – 5; (2)![]() 和 - 2.7
和 - 2.7
3. 比较 ![]() 和
和 ![]() 的大小.
的大小.
五、归纳小结
1. 绝对值 :在数轴上,一个数所对应的点与原点的距离叫做该数的绝对值.
2. 绝对值的性质:
(1)正数的绝对值是它本身;
(2)0负数的绝对值是它的相反数;
(3)0 的绝对值是 0.
因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成:
(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
3. 会利用绝对值比较两个负数的大小:两个负数,绝对值大的反而小.
![]()
略.
数学2.3 绝对值教案: 这是一份数学<a href="/sx/tb_c9910_t8/?tag_id=27" target="_blank">2.3 绝对值教案</a>,共6页。
北师大版七年级上册2.3 绝对值一等奖教案: 这是一份北师大版七年级上册2.3 绝对值一等奖教案,共5页。教案主要包含了总结归纳等内容,欢迎下载使用。
初中数学北师大版七年级上册2.3 绝对值精品教案: 这是一份初中数学北师大版七年级上册2.3 绝对值精品教案,共2页。教案主要包含了学习目标,学习过程,课堂小结等内容,欢迎下载使用。













