湘教版七年级下册1.3 二元一次方程组的应用获奖第1课时教学设计

这是一份湘教版七年级下册1.3 二元一次方程组的应用获奖第1课时教学设计，共5页。教案主要包含了知识与技能，过程与方法，情感态度，教学重点，教学难点，教学说明，归纳结论等内容，欢迎下载使用。
1.3  二元一次方程组的应用第1课时  用二元一次方程组解决较为简单的实际问题【知识与技能】1.通过实际问题使学生感受二元一次方程组的广泛应用，体会列二元一次方程组是解决某些实际问题的一种有效的数学模型，增强应用意识；2.能够由题意找出等量关系，列出二元一次方程组并检验所得结果是否符合实际意义.【过程与方法】教师引导学生的自主探索，体会把实际问题转化到数学方程问题的数学思想方法，加强知识的综合运用，培养学生分析问题和解决问题的能力.【情感态度】使学生体验数学活动充满探索与创造，体会到经济社会中数学的应用价值，提高学生探索的精神与能力.【教学重点】把应用问题转化为数学问题的过程，即对实际问题的数学模型的建立.【教学难点】在实践探索中寻找解题方案.一、情景导入，初步认知“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”你知道这四句话的意思吗？你能应用所学知识解决这个问题吗？分析：本题涉及的等量关系有：鸡头数+兔头数=      鸡的腿数+兔子的腿数=      解：设鸡有x只，兔子有y只，根据等量关系，得             答：笼中有23只鸡，12只兔.【教学说明】通过实际问题的引入，提高学生学习的兴趣.二、思考探究，获取新知1.某业余运动员针对自行车和长跑项目进行专项训练，某次训练中，他骑自行车的平均速度为10米每秒，跑步的平均速度为103米每秒，自行车路段和长跑路程共5千米，共用时15分钟，求自行车路段和长跑路段的长度.分析：本题涉及的等量关系有：自行车路段长度+长跑路段长度=总路程.骑自行车的时间+长跑时间=总时间.解：设自行车路段的长度为xm,长跑路段长度为ym，依题意得：答：自行车路段和长跑路段的长度分别为3000米、2000米.2.某食品厂要配制含蛋白质15%的食品100千克，现在有含蛋白质分别为20%、12%的甲、乙两种配料，用这两种配料可以配制出所要求的食品吗？如果可以的话，它们各需多少千克？分析：本问题涉及的等量关系有：甲配料质量+乙配料质量=总质量，甲配料含蛋白质质量+乙配料含蛋白质质量=总蛋白质质量.解：设含蛋白质20%的配料需要xkg,含蛋白质12%的配料需要ykg，依题意，得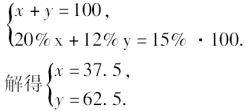答：可以配制出所要的食品，其中20%的配料需要37.5千克，12%的配料需要62.5千克.3.根据上面的两个例题，你能总结用二元一次方程组解决实际问题的步骤吗？【归纳结论】  用二元一次方程组解实际问题的步骤：(1)审题，分析题目中的已知与未知；(2)找出数量关系；(3)设未知数列方程组；(4)求解方程组；(5)检验；(6)写出答案.【教学说明】感受方程模型思想的必要性和优越性，并从列一元一次方程和列二元一次方程组的方法中，领会列二元一次方程组，思维方式的简洁明了性和在解一些等量关系较为复杂的应用题时体现的优越性.三、运用新知，深化理解1.如图：用8块相同的长方形拼成一个宽为48厘米的大长方形，每块小长方形的长和宽分别是多少？解：设小长方形的长是x厘米，宽是y厘米依题意得答：小长方形的长是36厘米，宽是12厘米.2.某服装厂接到生产一种工作服的订货任务，要求在规定期限内完成，按照这个服装厂原来的生产能力，每天可生产这种服装150套，按这样的生产进度在客户要求的期限内只能完成订货的；现在工厂改进了人员组织结构和生产流程，每天可生产这种工作服200套，这样不仅比规定时间少用1天，而且比订货量多生产25套，求订做的工作服是几套？要求的期限是几天？解：设订做的工作服是x套，要求的期限是y天，依题意，得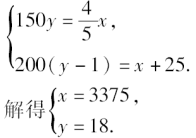答：订做的工作服是3375套，要求的期限是18天.3.甲、乙两人练习赛跑，如果甲让乙先跑10米，那么甲跑5秒钟就可以追上乙；如果甲让乙先跑2秒钟，那么甲跑4秒钟就能追上乙，求两人每秒钟各跑多少米？解：设甲的速度为x米/秒，乙的速度为y米/秒，依题意得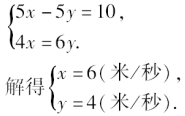答：甲的速度为6米/秒，乙的速度为4米/秒.4.某同学在A、B两家超市发现他看中的随身听的单价相同，书包单价也相同，随身听和书包单价之和是452元，且随身听的单价比书包单价的4倍少8元.(1)求该同学看中的随身听和书包单价各是多少元？(2)某一天该同学上街，恰好赶上商家促销，超市A所有商品打八折销售，超市B全场购物满100元返购物券30元销售(不足100元不返券，购物券全场通用)，但他只带了400元钱，如果他只在一家超市购买看中的这两样物品，你能说明他可以选择哪一家购买吗？若两家都可以选择，在哪一家购买更省钱？解：设书包的单价为x元，随身听的单价为y元，根据题意，得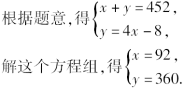答：该同学看中的随身听单价为360元，书包单价为92元.(2)在超市A购买随身听与书包各一件需花费现金：452×80%=361.6(元).因为361.6＜400，所以可以选择超市A购买.在超市B可先花费现金360元购买随身听，再利用得到的90元返券，加上2元现金购买书包，总计共需花费现金：360＋2＝362(元).因为362＜400，所以也可以选择在超市B购买.因为362＞361.6，所以在超市A购买更省钱.【教学说明】让学生通过练习巩固列二元一次方程组解应用题的技能.四、师生互动，课堂小结先小组内交流收获和感想，而后以小组为单位派代表进行总结.教师作以补充.1.布置作业:教材第18页“习题1.3”中第1、2、3、4、5题.2.完成同步练习册中本课时的练习.列二元一次方程组和列一元一次方程解实际问题，是用两种不同的表达形式揭示了问题中的相等关系；反过来，求解实际问题的实质是把问题中的相等关系翻译成数学表达式，从而把实际问题转化为数学问题.学习各类实际问题,不仅要熟悉各类问题的基本数量关系,而且还要弄清各类问题之间的本质联系.