初中数学湘教版七年级下册1.3 二元一次方程组的应用一等奖第2课时教案设计

第2课时  用二元一次方程组解决较复杂的实际问题

【知识与技能】

1.通过对实际问题的探索与解决,逐步形成结合具体事例情境发现,提出数学问题的能力；

2.学会用二元一次方程组解决简单的实际问题.

【过程与方法】

通过学生积极思考、互相讨论，经历探索事物之间的数量关系，形成方程模型.

【情感态度】

通过在解决实际问题的过程中同伴之间的讨论、交流与合作，体会与他人合作的重要性，逐步形成积极参与讨论、敢于发表见解并尊重与理解他人见解的合作意识.

【教学重点】

1.学生积极参与讨论和探究问题；

2.抽象出数学模型.

【教学难点】

用二元一次方程组解决较复杂的实际问题.

一、情景导入，初步认知

通过前面的学习,你能说出列二元一次方程组解决实际问题的步骤吗?其中什么是关键?

【教学说明】采用提问的形式，让学生对列二元一次方程组解决实际问题的步骤的复习，为本节课作铺垫.

二、思考探究，获取新知

1.小华从家里到学校的路是一段平路和一段下坡路.假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需要10min,从学校到家里需15min.问小华家离学校多远？

探究：(1)你能画线段表示本题的数量关系吗？

(2)列方程组；(在课本第16页填空)

(3)解方程组；

(4)检验写出答案.

讨论：本题是否还有其它解法？

2.某城市规定：出租车起步价所包含的路程为0至3千米，超过3千米的部分按每千米另收费，甲说“我乘这种出租车走了11千米，付了17元.”乙说“我乘这种出租车走了23千米，付了35元.”请你算一算：出租车的起步价是多少？超过3千米后，每千米的车费是多少元？

解：设出租车的起步价x元，超过3km后每千米收费y元，依题意，得

答：这种出租车的起步价是5元，超过3千米后每千米1.5元.

3.某装订车间的工人要将一批书打包后送往邮局，其中每包书的数目相等，第一次它们领来这批书的，结果打了14个包还多35本，第二次他们把剩下的书全部取来，连同第一次打包剩下的书一起，刚好又打了11包，那么这批书共有多少本？

解：设这批书共有x本，每包书有y本,依题意得

答：这批书共有1500本.

【教学说明】在学生探索解题方法的过程中，教师要鼓励学生多角度地思考，只要学生的方法有道理，就要给予肯定和鼓励，鼓励学生进行质问和大胆创新.

三、运用新知，深化理解

1.小明在拼图时，发现8个大小一样的长方形，恰好可以拼成如下图所示的一个大的长方形.小红看见了，说：“我来试一试”，结果小红拼成如下图所示的正方形，但中间还留有一个边长刚好为2mm的小正方形，你能解释一下吗？你能求出这些长方形的长和宽吗？

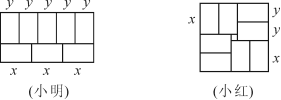
分析：①观察小明的拼图你能发现小长方形的长xmm与宽ymm之间的数量关系吗？

(根据矩形的对边相等，得3x=5y)

②再观察小红的拼图，你能写出表示小长方形的长xmm与宽ymm之间的另一个关系式吗？

(显然有x+2=2y)

8个小矩形的面积和=8xy=8×10×6=480(mm2)

大正方形的面积=x+2y2=10+2×62=484(mm2)484-480=4=22

因此小红拼出的大正方形中间还留下了一个恰好是边长为2mm的小正方形.

2.甲、乙两件服装的成本共500元，商店老板为获取利润，决定将甲服装按50%的利润定价，乙服装按40%的利润定价.在实际出售时，应顾客要求，两件服装均按9折出售，这样商店共获利157元，求甲、乙两件服装的成本各是多少元？

解：设甲服装的成本是x元，乙服装的成本是y元，依题意得

解得x=300，y=200.答：甲、乙两件服装的成本分别为300元、200元.

3.某工厂去年的总产值比总支出多500万元.由于今年总产值比去年增加15%，总支出比去年节约10%，因此，今年总产值比支出多950万元.今年的总产值和总支出各是多少万元？

分析：可列下表(去年总产值x万元，总支出y万元)：

题中有两个相等关系：(1)去年的总产值－去年的总支出＝500万元；(2)今年的总产值－今年的总支出＝950万元.

解：设去年的总产值是x万元，去年的总支出是y万元，由题意，得

所以(1＋15%)x＝2300，(1－10%)y＝1350.

故今年的总产值是2300万元，总支出是1350万元.

4.要用20张白卡纸做长方体的包装盒，准备把这些白卡纸分成两部分，一部分做侧面，另一部分做底面，已知每张白卡纸可以做2个侧面，或者3个底面，如果1个侧面和2个底面可以做成一个包装盒，那么如何分才能使做成的侧面和底面正好配套？

解：设用x张白卡纸做盒身，y张白卡纸做盒底盖，根据题意，得

由于解为分数，所以如果不允许剪开，则只能做成16个包装盒，无法全部利用；如果允许剪开，则分法很多，例如可以将一张白卡纸一分为二，用8张半做盒身，11张半做盒底盖，可以做成盒身17个，盒底盖34个，正好配套成17个包装盒，较充分地利用了材料.

【教学说明】让学生通过练习巩固列二元一次方程组解应用题的技能.

四、师生互动，课堂小结

先小组内交流收获和感想，而后以小组为单位派代表进行总结.教师作以补充.

1.布置作业:教材第19页“习题1.3”中第6、7、8、9题.

2.完成同步练习册中本课时的练习.

本节课通过师生交流，对学生的解法给予鼓励，并引导学生比较用二元一次方程组来解决实际问题的感受，从中体会到用二元一次方程组来解决实际问题比较方便.再通过练习使学生掌握如何从几何问题中抽象出数学模型.教学效果较好.