

初中数学湘教版七年级下册1.2.1 代入消元法一等奖教学设计
展开1.2 二元一次方程组的解法
1.2.1 代入消元法
![]()
【知识与技能】
会用代入消元法解简单的二元一次方程组.
【过程与方法】
经历探索代入消元法解二元一次方程的过程,理解代入消元法的基本思想所体现的化归思想方法.
【情感态度】
通过提供适当的情境资料,吸引学生的注意力,激发学生的学习兴趣;在合作讨论中学会交流与合作,培养良好的数学思想,逐步渗透类比、化归的意识.
【教学重点】
用代入消元法解二元一次方程组.
【教学难点】
探索如何用代入消元法解二元一次方程组,感受“消元”思想.
![]()
一、情境导入,初步认识
在上节课中,我们列出了二元一次方程组 ,并知道
,并知道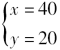 是这个方程组的一个解,这个解是这样得到的呢?
是这个方程组的一个解,这个解是这样得到的呢?
【教学说明】通过建构“问题情境”,使学生感受到问题是“现实的、有意义的、富有挑战性的”,让学生在不自觉中走进自己的最近“发展区”,愉悦地接受教学活动.
二、思考探究,获取新知
探究:解二元一次方程组
1.对于方程组![]() 方程①、②中的x都表示1月份的天然气费,y都表示1月份的水费,由此方程②中的x、y分别与方程①中的x、y的值相同.
方程①、②中的x都表示1月份的天然气费,y都表示1月份的水费,由此方程②中的x、y分别与方程①中的x、y的值相同.
由②式可得,x=y+20 ③.
于是可以把③代入①式,得
(y+20)+y=60 ④
解方程④,得 y=20,
把y的值代入③式,得x=40,
因此原方程组的解是![]()
2.解方程
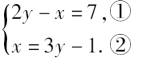
解:把②代入①,得 2y-(3y-1)=7
解得y= -6
把y= -6代入②中,得 x= -19.
所以原方程组的解为
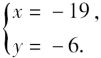
【归纳结论】 解二元一次方程组的基本想法是:消去一个未知数(简称为消元),得到一个一元一次方程,然后解这个一元一次方程.
在上面的例子中,消去一个未知数的方法是:把其中一个方程的某一个未知数用含有另一个未知数的代数式表示,然后把它代入到另一个方程中,便得到一个一元一次方程,这种解方程组的方法叫做代入消元法,简称代入法.
3.解方程组
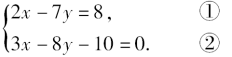
观察分析此方程组与2中的方程组在形式上的差别. 易知2的方程组中直接将一个方程移项后代入另外一个方程, 而此方程组中两个方程未知数的系数都不是1,不能直接代入, 这时怎么办呢? 能不能将其中一个方程适当变形, 用一个未知数来表示另一个未知数?显然, 这个变形是能够办到的. 我们有两个办法, 一个是某个方程两边同除以某个未知数的系数, 使这个未知数的系数化1, 化成例1的形式;另一个是将某个方程的某一个未知数移到方程的一边, 其他各项移到另一边 ,再把这个未知数的系数化1, 从而达到“用一个未知数来表示另一个未知数”的目的 .
显然第二种方法更为直接, 因而考虑方程中各项的系数, 选择一个系数比较简单的方程. 易见①比较简单, 所以将方程①中的x用y来表示 .
解:由①, 得 x=4+![]() y,③
y,③
将③代入②, 得
3(4+![]() y)-8y-10=0, y=-0.8 .
y)-8y-10=0, y=-0.8 .
将y=-0.8代入③, 得 x=1.2.
所以方程组的解是x=1.2,y=-0.8.
【教学说明】这里是先消去x ,得到关于y的一元一次方程 ,可不可以先消去y呢?(让学生试一试, 并比较两种解法的优劣. 易知先消去x使变形后的方程比较简单和代入后化简比较容易.)
由上面的解题过程,你能总结出用代入法解二元一次方程组的步骤吗?
【归纳结论】 代入法解二元一次方程组的步骤:
(1)将方程组中的一个方程变形,使得一个未知数能用含另一未知数的代数式表示.
(2)把这个代数式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值.
(3)把这个未知数的值代入代数式,求另一未知数的值.
(4)写出方程组的解.
三、运用新知,深化理解
1.见教材P7例2.
2.方程-x+4y=-15用含y的代数式表示x是( C )
A.-x=4y-15 B.x=-15+4y
C.x=4y+15 D.x=-4y+15
3.将y=-2x-4代入3x-y=5可得( B )
A.3x-2x+4=5 B.3x+2x+4=5
C.3x+2x-4=5 D.3x-2x-4=5
4.见教材P7例1.
5.用代入法解方程组![]() 有以下过程:
有以下过程:
(1)由①得x=![]() ③;
③;
(2)把③代入②得3×![]() -5y=5;
-5y=5;
(3)去分母得24-9y-10y=5;
(4)解之得y=1,再由③得x=2.5.其中错误的一步是( C )
A.(1) B.(2) C.(3) D.(4)
6.把下列方程写成用含x的代数式表示y的形式:
(1) 3x+4y-1=0;
(2)5x-2y+9=0
分析:即将方程作适当的变形, 把含有y的项放在方程的一边, 其他的项移到方程另一边, 再把y的系数化1.



【教学说明】通过不同题型考察代入法解方程组,从而加强对所学知识点的巩固提高,加深对所学知识的理解与应用.
四、师生互动,课堂小结
先小组内交流收获和感想而后以小组为单位派代表进行总结.教师作以补充.
![]()
1.布置作业:教材第12页“习题1.2”中第1题.
2.完成同步练习册中本课时的练习.
![]()
本课按照“数学问题引入——寻求一元一次方程的解法——探索二元一次方程组的代入消元法——典型例题——归纳代入法”的一般步骤的思路进行设计.在教学过程中,充分调动学生的主观能动性和发挥教师的主导作用,坚持启发式教学.教师创设有趣的情境,引发学生自觉参与学习活动的积极性,将发现知识的过程融于有趣的活动中.重视知识的发生过程.将设未知数列一元一次方程的求解过程与二元一次方程组相比较,从而得到二元一次方程组的代入(消元)解法,这种比较,可使学生在复习旧知识的同时,使新知识得以掌握,这对于学生体会新知识的产生和形成过程是十分重要的.
初中数学湘教版七年级下册第1章 二元一次方程组1.2 二元一次方程组的解法1.2.1 代入消元法教学设计: 这是一份初中数学湘教版七年级下册<a href="/sx/tb_c24993_t8/?tag_id=27" target="_blank">第1章 二元一次方程组1.2 二元一次方程组的解法1.2.1 代入消元法教学设计</a>,共5页。教案主要包含了知识与技能,过程与方法,情感态度,教学重点,教学难点,教学说明,归纳结论等内容,欢迎下载使用。
七年级下册第1章 二元一次方程组1.2 二元一次方程组的解法1.2.1 代入消元法教案: 这是一份七年级下册<a href="/sx/tb_c24993_t8/?tag_id=27" target="_blank">第1章 二元一次方程组1.2 二元一次方程组的解法1.2.1 代入消元法教案</a>,共4页。教案主要包含了情景展示,温故导新,教学新知,启智赋能,例题示范,学会应用,做一做,基础巩固,能力提升等内容,欢迎下载使用。
初中数学湘教版七年级下册1.2.2 加减消元法优秀第2课时教案设计: 这是一份初中数学湘教版七年级下册1.2.2 加减消元法优秀第2课时教案设计,共8页。













