初中数学人教版九年级上册第二十一章 一元二次方程21.2 解一元二次方程21.2.3 因式分解法完整版ppt课件

九年级上册21.2.3因式分解法解一元二次方程分层练习

【基础篇】

一、选择题

1．方程x(x－2)＝2(2－x)的根为(    )

A．x＝－2                    B．x＝2

C．x1＝2，x2＝－2             D．x1＝x2＝2

2．方程(x－1)2＝1－x的根为(    )

A．0         B．－1和0          C．1           D．1和0

3．若实数x、y满足(x－y)(x－y＋3)＝0，则x－y的值是(    )

A．－1或－2        B．－1或2         C．0或3         D．0或－3

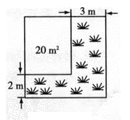
4．如图，将一块正方形空地划出部分区域进行绿化，原空地一边减少了2m，另一边减少了3m，剩余一块面积为20m2的矩形空地，则原正方形空地的边长是（    ）

A．7m          B．8m         C．9m              D．10m

5．已知三角形的两边长是方程x2－5x+6＝0的两个根，则该三角形的周长L的取值范围是（    ）

A．1<L<5               B．2<L<6

C．5<L<9               D．6<L<10

二、填空题

6．在实数范围内定义一种运算“*”，其规则为a*b＝a2－b2，根据这个规则，知方程(x－2)*1＝0的解为_____________．

7．如果x2－x－1＝（x+1）0，那么x的值为_____________．

三、解答题

8．解方程3x(x－2)＝2(x－2)               9．解方程x2－4x＋4＝(2－3x)2

10．解方程(2y－1)2＝3(1－2y)．

【能力篇】

11．阅读下面材料：

把方程x2－4x+3＝0写成x2－4x+4－4+3＝0，(x－2)2－1＝0．

因式分解，得(x－2+1)(x－2－1)＝0，

(x－1)(x－3)＝0．

发现：(－1)+(－3)＝－4，(－1)×(－3)＝3．

结论：方程x2－(p+q)x+pq＝0可变形为(x－p)·(x－q)＝0．

应用上面的解题方法，解下列方程：

（1）x2+5x+6＝0；         （2）x2－7x+10＝0；

（3）x2－5x－6＝0；       （4）x2+3x－4＝0．

【拔高篇】

12．已知：关于x的一元二次方程x2+2x+k＝0有两个不相等的实数根．

（1）求k的取值范围；

（2）当k取最大整数值时，用合适的方法求该方程的解．

参考答案

1．C

2．D

3．D

4．A 

5．D 

6．

7．2

8．x1＝2，

9．x1＝0，x2＝1

10．解：原方程可化为(2y－1)2－3(1－2y)＝0，

因式分解，得(2y－1)(2y+2)＝0．∴，y2＝－1．

11．解：（1）方程变形为(x+2)(x+3)＝0，

∴x1＝－2，x2＝－3．

（2）方程变形为(x－2)(x－5)＝0，

∴x1＝2，x2＝5．

（3）方程变形为(x－6)(x+1)＝0，

∴x1＝6，x2＝－1．

（4）方程变形为(x+4)(x－1)＝0，

∴x1＝－4，x2＝1．

12．解：（1）由题意可得∆＝22－4k>0，

解得k<1．

（2）由（1）中的k<1得k取的最大整数值为0，即k＝0，

当k＝0时，原方程可化为x2+2x＝0，

∴x(x+2)＝0，

解得x1＝0，x2＝－2．