22.4.4 第5讲《二次函数的最值问题》专项复习 课件+教案+分层练习+预习检测

九年级上册22.4.4第5讲 二次函数的最值问题

专项复习预习检测

测试题1  点M（－3，4）离原点的距离是（    ）单位长度.

A. 3          B. 4           C. 5             D. 7

答案：C

测试题2  若点P为y轴上的一点，且点P到点A（4，3）、点B（2，－1）的距离和最小，则点P的坐标为（    ）

A. （0，）            B. （0，）

C. （0，）               D. （0，0）

答案：C

解析过程：∵A（4，3），

∴点A关于y轴的对称点A′的坐标为（-4，3），

设直线A′B的解析式为y=kx+b（k≠0），

则，解得，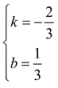

∴直线A′B的解析式为，

∴P（0，）．

故选C．

测试题3  直线y=3x-2和直线y=2x+3与y轴所围成的图形的面积为（    ）

A.         B.              C. 15            D.  25

答案：B

解析过程：如图所示，在同一直角坐标系中画出两条直线的图象，过点C作CD⊥y轴于点D.

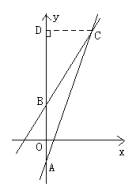
联立，解得

交点C的坐标为（5，13）

直线与分别与y轴交于点A（0，-2）和点B（0，3），

又∵CD=5，

.

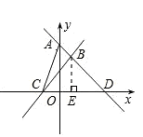
测试题4  如图，直线轴交于点A，与x轴交于点D，与直线交于点B，且直线与x轴交于点C，则△ABC的面积为（    ）

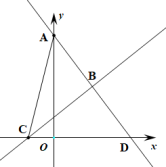
A. 0.5          B. 4           C.8           D. 2

答案：B

解析过程：直线轴交于点A，与x轴交于点D，

则令x＝0,则y＝4,故A点的坐标为(0,4)，

则令y＝0,即＝0,x＝3,则D点的坐标为(3,0)，

直线与轴交于点C，则C点坐标为(－1,0)，

因为直线与直线交于点B,

所以列出方程组得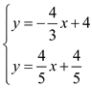，解得，故B点坐标为(1.5，2).

故＝.

测试题5 已知二次函数y=ax2+bx+c同时满足下列条件：①对称轴是x=1；②最值是15；③二次函数的图象与x轴有两个交点，其横坐标的平方和为15－a．则b的值是（    ）

A.  4或－30          B. －30

C. 4             D.  6或－20

答案：C

解析过程：由题意可设该抛物线解析式为y=a(x－1)2+15，

化为一般式为y=ax2－2ax+a+15，

x1+x2=2，x1x2=，

所以，

解得a1=15，a2=-2

由△＞0舍去a=15，

所以a=-2，b=－2a=4，故选C．