












人教版九年级上册24.1.4 圆周角精品课件ppt
展开九年级上册24.1.4圆周角教案
学习目标:
1.掌握圆周角定理及其推论.
2.会用圆周角定理及其推论进行证明和计算.
3.掌握并运用圆内接四边形的性质.
学习重难点:
重点:圆周角定理及其推论.
难点:运用圆周角定理及其推论解决有关问题.
一、复习回顾
弧、弦、弦信距、圆心角之间有什么关系?
二、情境导入
在圆中,除圆心角外,还有一类特殊的角——圆周角,它又有什么性质呢?
三、知识讲解
1.圆周角
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
圆周角必须具备两个条件:①顶点在圆上;②两边都与圆相交.

2.圆周角定理
圆周角∠BAC与∠BOC对着同一条弧![]() ,它们之间存在什么关系呢?下面我们就来研究这个问题。
,它们之间存在什么关系呢?下面我们就来研究这个问题。

我们来分析第(1)种情况.如图(1),
圆心O在∠BAC的一条边上.
![]() A.
A.
对于第(2)(3)种情况,可以通过添加辅助线(图(2)(3)),将它们转化为第(1)种情况,从而得到相同的结论.
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
符号语言
∵∠A是![]() 所对的圆周角,∴∠A=½∠BOC
所对的圆周角,∴∠A=½∠BOC
推论
同弧或等弧所对的圆周角相等,半圆(或直径)所对的圆周角是直角.90°的圆周角所对的弦是直径(如图).


符号语言
∵∠C、∠D是![]() 所对的圆周角,∴∠C=∠D.
所对的圆周角,∴∠C=∠D.
∵∠C是AB是直径(或![]() )所对的圆周角,∴∠C=90°.
)所对的圆周角,∴∠C=90°.
∵∠C=90°,∴∠C所对的弦(或弧)是直径(或半圆)
敲黑板划重点
(1)因为圆中一条弦所对的圆周角的大小有两种情况,所以不能根据弦相等得到圆周角相等.
(2)在同圆或等圆中,一条弦所对的圆周角相等或互补,即圆周角在弦的同侧相等,异侧互补,如图,∠C,∠D,∠E都是弦AB所对的圆周角.∠C、∠D在弦AB的同侧,则∠C=∠D;∠D、∠E在弦AB的异侧,则∠D+∠E=180°.
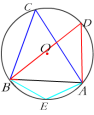
3.圆内接四边形的性质
圆内接多边形:如果一个多边形的所有顶点都在圆上,这个多边形叫做圆的内接多边形,这个圆叫做多边形的外接圆.

如图,连接OB、OD.
∵∠A所对的弧为![]() ,∠C所对的强为
,∠C所对的强为![]() ,
,
∴![]() 和
和![]() 所对的圆心角的和是周角.
所对的圆心角的和是周角.
∠A+∠C=½×360°=180°.
同理∠B+∠D=180°.
圆内接四边形性质:圆内接四边形的对角互补
四、例题精讲
1.利用圆周角定理及推论进行计算或证明
例1如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°.求证:∆ABC是等边三角形.
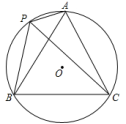
方法总结
利于同弧所对的圆周角相等,在圆中起到转化角的关键作用.
变式训练
如图,⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为( )
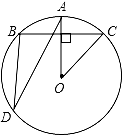
A.15° B.25° C.30° D.50°
2.圆圆内接四边形的性质
例2如图,四边形ABCD内接于⊙O,并且AD是⊙O的直径,C是弧BD的中点,AB和DC的延长线交⊙O外一点E.求证:BC=EC.
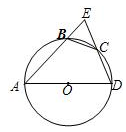
方法总结
利用圆的内接四边形的性质和等弧所对的圆周角相等进行角的转换,在利用等角对等边得到线段相等.
变式训练
如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD·DC=PA·BC.

深入探究
如图,△ABC内接于⊙O,AB为⊙O的直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.
求证:(1)∠DAC=∠DBA;
(2)点P是线段AF的中点.

我的收获
__________________________________________________________________________________________________________________________________________________________
数学九年级上册24.1.4 圆周角背景图课件ppt: 这是一份数学九年级上册24.1.4 圆周角背景图课件ppt,共18页。PPT课件主要包含了合作探究,知识点一,知识点二,∠ACB,∠AOB,∠A∠C,精炼提升,知识点三,COA,同弧或等弧等内容,欢迎下载使用。
人教版七年级上册4.3.1 角教学ppt课件: 这是一份人教版七年级上册4.3.1 角教学ppt课件,共20页。PPT课件主要包含了知识回顾,创设情境引入新知,自主预习,自主探究,角的表示,知识梳理,随堂练习,填一填等内容,欢迎下载使用。
初中数学人教版九年级上册24.1.4 圆周角集体备课ppt课件: 这是一份初中数学人教版九年级上册24.1.4 圆周角集体备课ppt课件,共21页。PPT课件主要包含了请你评一评,请你记一记,思考与探索,O在∠BAC内,O在∠BAC边上,O在∠BAC外,议一议,典型例题,练一练,同弧所对的圆周角相等等内容,欢迎下载使用。














