
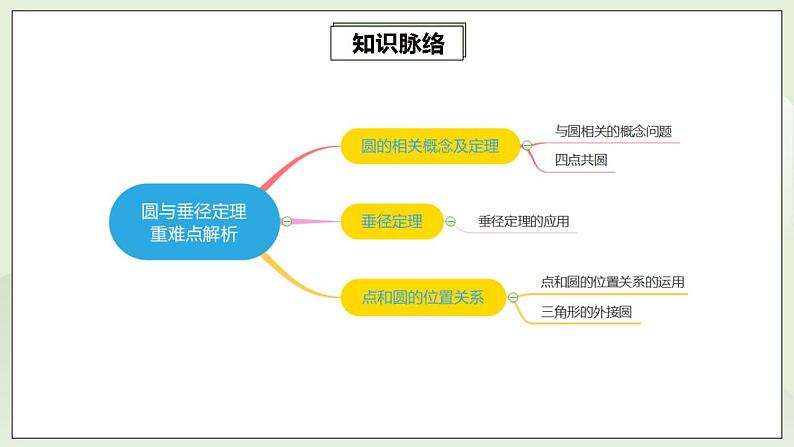
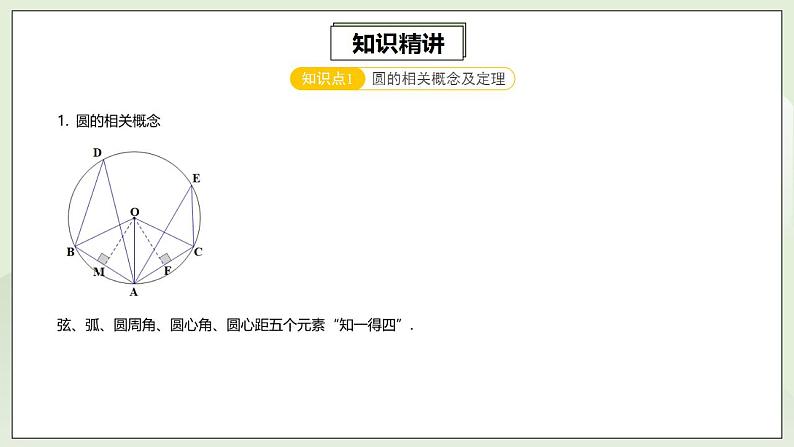
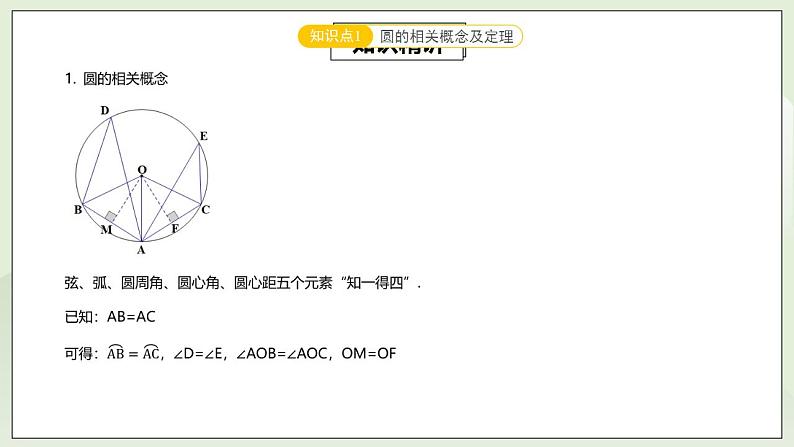
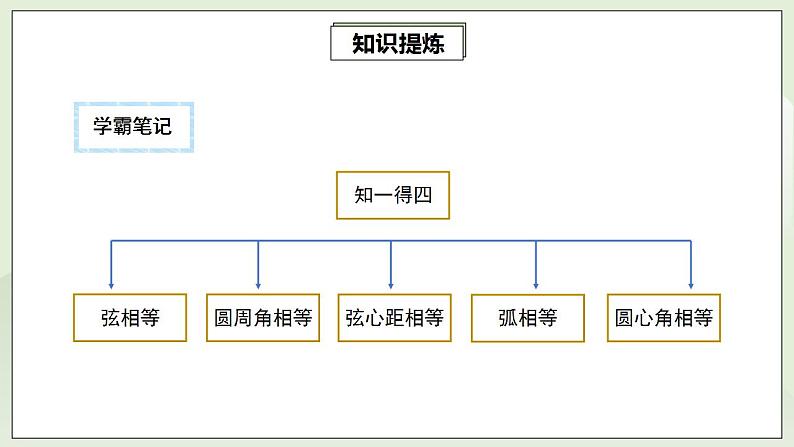






24.5.1第7讲《圆与垂径定理》重难点解析 课件+教案+分层练习+预习检测
展开九年级上册24.5.1第7讲《圆与垂径定理》重难点解析分层练习
【基础篇】
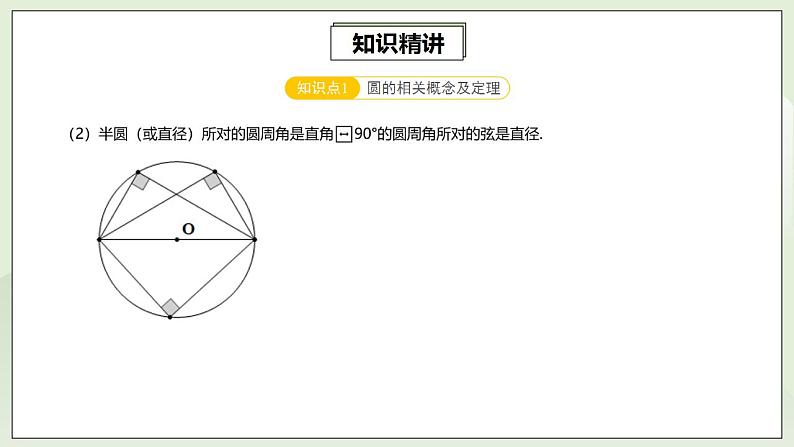
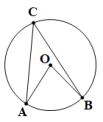
测试题1 如图,∠AOB是⊙O的圆心角,∠AOB=80°则弧AB所对圆周角∠ACB的度数是( )
A. 40° B. 45° C. 50° D. 80°
答案:A
解析过程:∵∠ACB与∠AOB同对着弧AB ,
而∠ACB为圆周角,∠AOB为圆心角;
∴∠ACB= ![]()
故选A.
测试题2 如图,AB是⊙O的直径,CD为弦,CD⊥AB且相交于点E,则下列结论中不成立的是( )

A. ∠A=∠D B. ![]()
C. ∠ACB=90° D. ∠COB=3∠D
答案:D
解析过程:∵![]() 与
与![]() 都是
都是![]() 所对的圆周角,∴
所对的圆周角,∴![]() ,∴A正确;
,∴A正确;
∵![]() 是
是![]() 的直径,
的直径,![]() 为弦,
为弦,![]() ,∴
,∴![]() ,∴B正确;
,∴B正确;
∵![]() 是
是![]() 的直径,∴
的直径,∴![]() ,∴C正确;
,∴C正确;
∵![]() 与
与![]() 分别是
分别是![]() 所对的圆心角与圆周角,∴
所对的圆心角与圆周角,∴![]() ,∴D错误,故选D.
,∴D错误,故选D.
测试题3 如图,△ABC内接于⊙O,若∠ACB=60°,则∠OAB的度数等于( )

A. 20° B. 25° C. 30° D. 35°
答案:C
解析过程:∵∠ACB=60°,
∴∠AOB=2∠ACB=120°,
而OA=OB,
∴∠OAB=∠OBA,
∴∠OAB=![]() ×(180°﹣120°)=30°.
×(180°﹣120°)=30°.
故选C.
【能力篇】
测试题4 如图,AB是⊙O的直径,若AC=4,∠D=60°,则AB= .
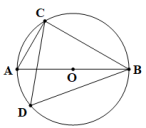
解析过程:由题意得∠A=∠D=60°,∠ACB=90°
∴∠ABC=30°
∵AC=4
∴AB=8.
【拔高篇】
测试题5 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D 为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.

解析过程:(1)∵OD⊥AC、OD为半径
∴弧CD=弧AD
∴∠CBD=∠ABD
∴BD平分∠ABC.
(2)∵OB=OD,
∴∠OBD=∠ODB=30○
∴∠AOD=∠OBD=∠ODB=30○+30○=60○
又∵OD⊥AC于E.
∴∠OEA=90○
∴∠A=180○-∠OEA-∠AOD =180○-90○-60○
又∵AB为⊙O的直径,
∴∠ABC=90○,则在RT△ABC中BC=![]() AB
AB
∵OD=![]() AB
AB
∴BC=OD.










