














24.5.4第10讲《圆中线段长度求解问题》专项复习 课件+教案+分层练习+预习检测
展开九年级上册24.5.4 第10讲《圆中线段长度求解问题》
专项复习预习检测
测试题1 如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是![]() cm,则这个正六边形的周长是( )
cm,则这个正六边形的周长是( )

A. 6![]() cm B. 12cm
cm B. 12cm
C. ![]() cm D. 36cm
cm D. 36cm
答案:C
解题过程:连接OA,OB.则![]() ,
,![]() 为等边三角形,正六边形ABCDEF的半径是
为等边三角形,正六边形ABCDEF的半径是![]() cm,即OA=
cm,即OA=![]() cm,则AB=
cm,则AB=![]() cm,正六边形的周长为
cm,正六边形的周长为![]()
![]() .故本题选C.
.故本题选C.
测试题2 如图所示的圣诞帽呈圆锥形,其母线长为2,底面半径为1,则它的侧面积为( )

A. 2 B. π C. 2π D. 4π
答案:C
解题过程:∵圆锥的底面圆的半径为1,
∴圆锥的底面圆的周长=2π×1=2π,
∴圆锥的侧面积=![]() ×2π×2=2π.
×2π×2=2π.
故选:C.
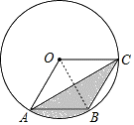
测试题3 如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )

A. 6π B. 3![]() π C. 2
π C. 2![]() π D. 2π
π D. 2π
答案:A
解析过程:连接OB,
∵四边形OABC是平行四边形,
∴AB=OC,
∴AB=OA=OB,
∴△AOB是等边三角形,
∴∠AOB=60°,
∵OC∥AB,
∴S△AOB=S△ABC,
∴图中阴影部分的面积=S扇形AOB=![]() =6π,
=6π,
故选A.
测试题4 如图,一正方形同时外切和内接于两个同心圆,当小圆的半径为r时,大圆的半径为( )
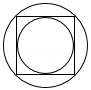
A. ![]() r B. 1.5r C.
r B. 1.5r C. ![]() r D. 2r
r D. 2r
答案:A
解析过程:如图,连接OD、OE、OF,
则:OE=OF=r,
∵正方形ABCD切小圆于E、F,
∴∠OED=∠OFD=∠D=90°,
∴四边形OEDF是正方形,
∴OE=DE=r,
在△OED中由勾股定理得:OD=![]() =
=![]() r,
r,
即大圆的半径是![]() r.
r.
故选A.

测试题5 如果一个正三角形与一个正六边形的面积相等,那么它们的周长之比是( )
A. 1:2 B. ![]() :2 C.
:2 C. ![]() :2 D.
:2 D. ![]() :3
:3
答案:C
解析过程:设正三角形的边长为2a,正六边形的边长为2b
(1)过A作AD⊥BC与D,则∠BAD=30°,
AD=AB•cos30°=![]() a,
a,
∴S△ABC=![]() BC•AD=
BC•AD=![]() ×2a×
×2a×![]() a=
a=![]() a2;
a2;
(2)连接OA、OB,过O作OD⊥AB;
∵∠AOB=360°÷6=60°,
∴∠AOD=30°,
OD=ADtan30°=![]() b,
b,
∴S△OAB=![]() ×2b×
×2b×![]() b=
b=![]() b2,
b2,
∴S六边形=6S△OAB=6×![]() b2=6
b2=6![]() b2,
b2,
∵正三角形与一个正六边形的面积相等,
∴![]() a2=6
a2=6![]() b2
b2
∴a:b=![]() :1.
:1.
∴周长之比为![]() :2,
:2,
故选C.











