第12章 全等三角形素养集训 角平分线中作辅助线的四种常用方法 课件

这是一份第12章 全等三角形素养集训 角平分线中作辅助线的四种常用方法 课件，共13页。

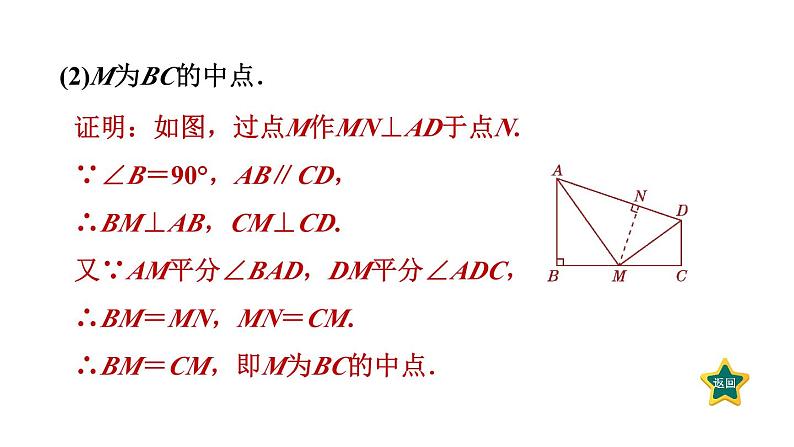
角平分线中作辅助线的四种常用方法素养集训第十二章 全等三角形答案显示见习题见习题见习题见习题1．【教材P52习题T7改编】如图，在四边形ABCD中，∠B＝90°，AB∥CD，M为BC边上的一点，且AM平分∠BAD，DM平分∠ADC.求证：(1)AM⊥DM；证明：∵AB∥CD，∴∠BAD＋∠ADC＝180°.∵AM平分∠BAD，DM平分∠ADC，∴∠BAM＝∠MAD，∠CDM＝∠ADM.∴2∠MAD＋2∠ADM＝180°.∴∠MAD＋∠ADM＝90°.∴∠AMD＝90°，即AM⊥DM.证明：如图，过点M作MN⊥AD于点N.∵∠B＝90°，AB∥CD，∴BM⊥AB，CM⊥CD.又∵AM平分∠BAD，DM平分∠ADC，∴BM＝MN，MN＝CM.∴BM＝CM，即M为BC的中点．(2)M为BC的中点．2．如图，在四边形ABCD中，BC＞AB，AD＝DC，BD平分∠ABC.求证：∠C＋∠BAD＝180°.【点方法】本题运用转化思想进行证明．当遇到证明两角的和是180°的问题时，往往将其转化为证明平角或三角形内角和的问题．本题根据角平分线的性质想到从点D向∠ABC的两边作垂线段，构造直角三角形，证明两个直角三角形全等，从而将两个角的和转化为一个平角，进而得出结论．3．如图，在△ABC中，AB＝CB，∠ABC＝90°，D是AB上一点，AE⊥CD于点E，且AE＝ CD，BD＝8 cm.求点D到AC的距离．【点方法】本题综合考查了三角形全等的判定与性质和角的平分线的性质，解决本题的关键是证明CD平分∠ACB.可以通过添加辅助线构造全等三角形来证明角相等，再由角的平分线的性质求得结论.4．【2022·太原师范附属中学月考】如图，在△ABC中，AD平分∠BAC，∠C＝2∠B.求证：AC＋CD＝AB.【点拨】由AD平分∠BAC考虑将△ACD“折叠”，构造全等三角形．证明：如图，在AB上截取AE＝AC，连接DE，过点E作EF⊥BD于点F，易证△AED≌△ACD.