初中数学人教版九年级上册24.1.1 圆图文ppt课件

这是一份初中数学人教版九年级上册24.1.1 圆图文ppt课件，共26页。PPT课件主要包含了各角相等但各边不相等，轴对称，中心对称，∴∠A∠B，B-20，E20等内容，欢迎下载使用。
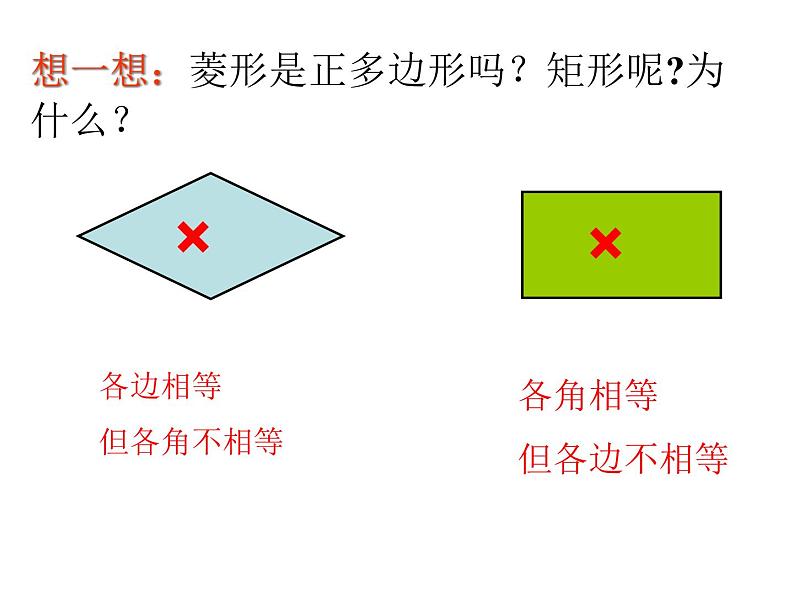
想一想：菱形是正多边形吗？矩形呢?为什么？
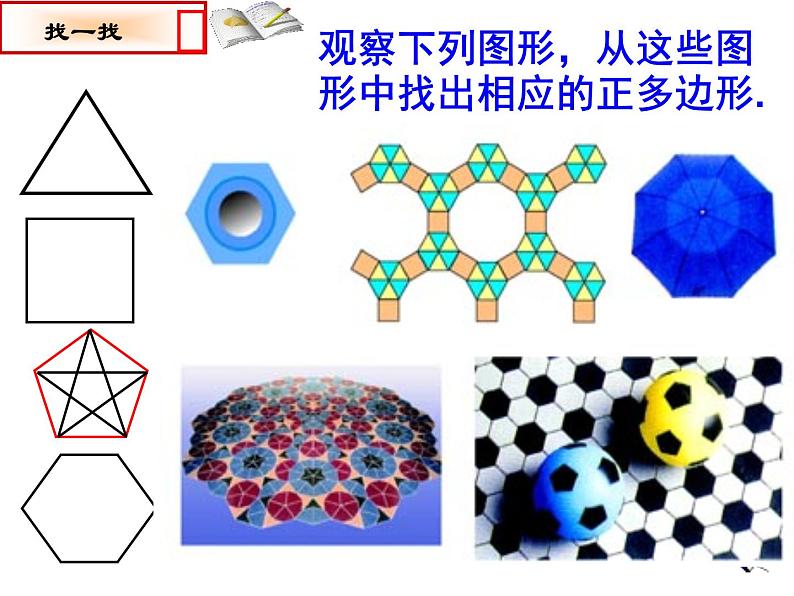
观察下列图形，从这些图形中找出相应的正多边形.
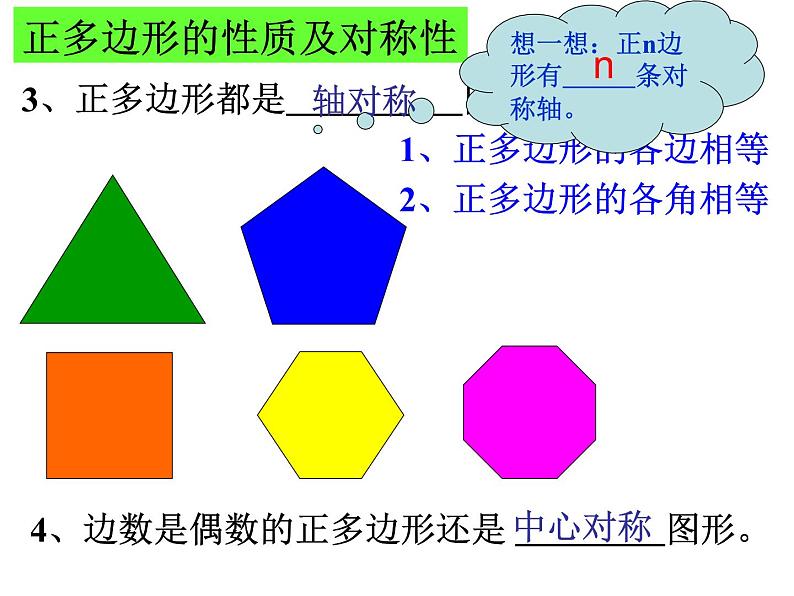
3、正多边形都是 图形。
正多边形的性质及对称性
4、边数是偶数的正多边形还是 图形。
1、正多边形的各边相等
2、正多边形的各角相等
想一想：正n边形有 条对称轴。
正n边形的每一个内角的度数都是____________;外角是___________;
正n边形的边长为a,它的周长是 。
①正五边形的内角和为 ，每个内角的度数为 。②若一个正多边形的外角是30度，则这个正多边形是正 边形。
观察下列多边形的边数和形状，我发现 。
正n边形的边数越多,形状就越接近于圆
人教版九年级（上）数学
24.3 正多边形和圆
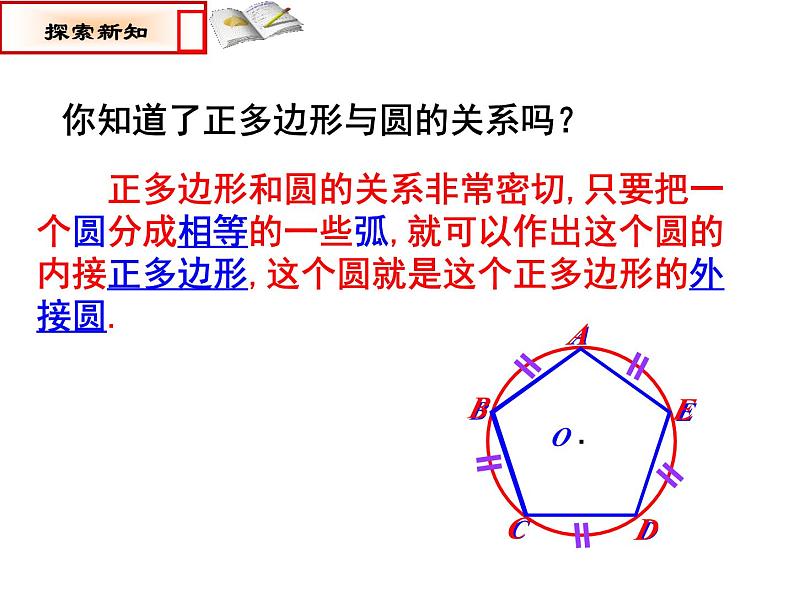
你知道了正多边形与圆的关系吗？
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
如图,把⊙O分成相等的6段弧,依次连接各分点得到正六边形ABCDEF.
∴ AB=BC=CD=DE=EF=FA,
同理∠B=∠C=∠D=∠E =∠F
又∵六边形ABCDEF的顶点都在⊙O上,
∴ 六边形ABCDEF是⊙O的内接正六边形, ⊙O是六边形ABCDE的外接圆.
我们以圆内接正六边形为例证明.
归纳：如果将一个圆n等分，依次连接各分点得到一个n边形，这个n边形一定是正n边形
弦相等（多边形的边相等）弧相等 圆周角相等（多边形的角相等）
③正多边形每一边所对的圆心角叫做正多边形的中心角
①我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心
②外接圆的半径叫做正多边形的半径
④中心到正多边形的一边的距离叫做正多边形的边心距
想一想：正多边形的中心角和外角有什么关系？
设正n边形的边长为a,半径为R,边心距为r,它的周长为 ，面积为 。
如图，正六边形ABCDEF的外接圆半径为4，求这个正六边形的中心角、边长、周长和面积各是多少？　
智慧背囊：正多边形边长的一半、半径、边心距构成了一个直角三角形，正多边形的有关计算都可以化归到这个直角三角形中。
有一个亭子,它的地基半径为4 m的正六边形,求地基的周长和面积(精确到0.1 m2).
解: 如图由于ABCDEF是正六边形,所以它的中心角等于 ，△OBC是等边三角形，从而正六边形的边长等于它的半径.
l =4×6=24(m).
利用勾股定理,可得边心距
要用半径为8cm圆形木板截出一个正方形模具，则所截的正方形模具的边长最长应为_____________cm．
1．正八边形的每个内角是______度.
2．如图，正六边形ABCDEF内接于⊙O，则∠CFD的度数是（ ） A. 60° B. 45° C. 30° D. 22.5°
4．如图，正六边形ABCDEF的半径为2，以它的中心O为坐标原点，顶点B、E在x轴上，求正六边形ABCDEF的各顶点的坐标．
A基础达标1、已知正三角形、正方形、正六边形的半径都是R，请你将各正多边形的边长、边心距、周长和面积值填在下表中．（用R来表示）2、圆内接正六边形一边所对的圆周角是（ ）（A）30．（B）60．（C）150．（D）30或150．3、若一个正多边形的每个内角的度数是中心角的3倍，则正多边形的边数是（ ）（A）4．（B）6．（C）8．（D）12．
B感受中考4、如图，有一个边长为1.5cm的正六边形，如果要剪一张圆形纸片完全盖住这个图形，那么这张圆形纸片的最小半径为___________cm． 5、已知圆内接正六边形的边长是1，则这个圆的内接正方形的边长是____________．
从正五角星形的内角谈起 我们常见到的五星红旗上的五角星形，不但给庄严的感觉，而且还给人一种和谐、对称、协调的美感，很容易得到它的一个内角为36． 我们将圆周五等分，得五个分点1、2、3、4、5，如果按1→2→3→4→5相连，则得一个正五边形（如图①）．如果按1→3→5→2→4→1相连，则得一个正五角星形（如图②）．前者看成是5/1边形，后者则可以看成是5/2边形． 所以每一个内角为． 图① 图② 图③ 图④ 以此类推，如图③、④将两个七角星形分别看成7/2边形和7/3边形，其内角分别为 ， ．有兴趣的同学不妨继续沿着这个思路研究下去，你一定会有很大的收获．
1.课本P107第1题