2022-2023学年广东省河源市连平县七年级（下）期末数学试卷（含解析）

这是一份2022-2023学年广东省河源市连平县七年级（下）期末数学试卷（含解析），共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年广东省河源市连平县七年级（下）期末数学试卷
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列长度的三条线段中，能组成三角形的是(    )
A. 1，1，3 B. 1，4，3 C. 2，6，3 D. 6，9，6
2. 人体中枢神经系统中含有1千亿个神经元.某个神经元的直径约为52微米，52微米为5.2×10−5米.将5.2×10−5用小数表示为(    )
A. 0.0052 B. 0.00052 C. 0.000052 D. 0.0000052
3. 吴老师在演示概率试验时，连续随机抛掷一枚质地均匀的骰子，前3次的结果是“6”，则第4次的结果是“6”的概率是(    )
A. 0 B. 16 C. 12 D. 1
4. 如图，点D，E分别在线段AB，AC上，BE与CD相交于点N.若△ABE≌△ACD，且∠A=65°，∠C=15°，则∠AEB的度数为(    )
A. 80°
B. 90°
C. 100°
D. 105°
5. 下列计算正确的是(    )
A. a3⋅a2=a6 B. a3+a2=2a5 C. (3a3)2=9a6 D. a8÷a2=a4
6. 油箱中存油20升，油从油箱中均匀流出，流速为0.2升/分钟，则油箱中剩余油量Q(升)与流出时间t(分钟)的关系式是(    )
A. Q=0.2t(0≤t≤100) B. Q=20−0.2t(0≤t≤100)
C. t=0.2Q(0≤Q≤20) D. t=20−0.2Q(0≤Q≤20)
7. 如图，把一张长方形的纸按图那样折叠后，B，C两点落在B1，C1处，若∠AEB1=70°，则∠BEF=(    )
A. 70°
B. 60°
C. 65°
D. 55°
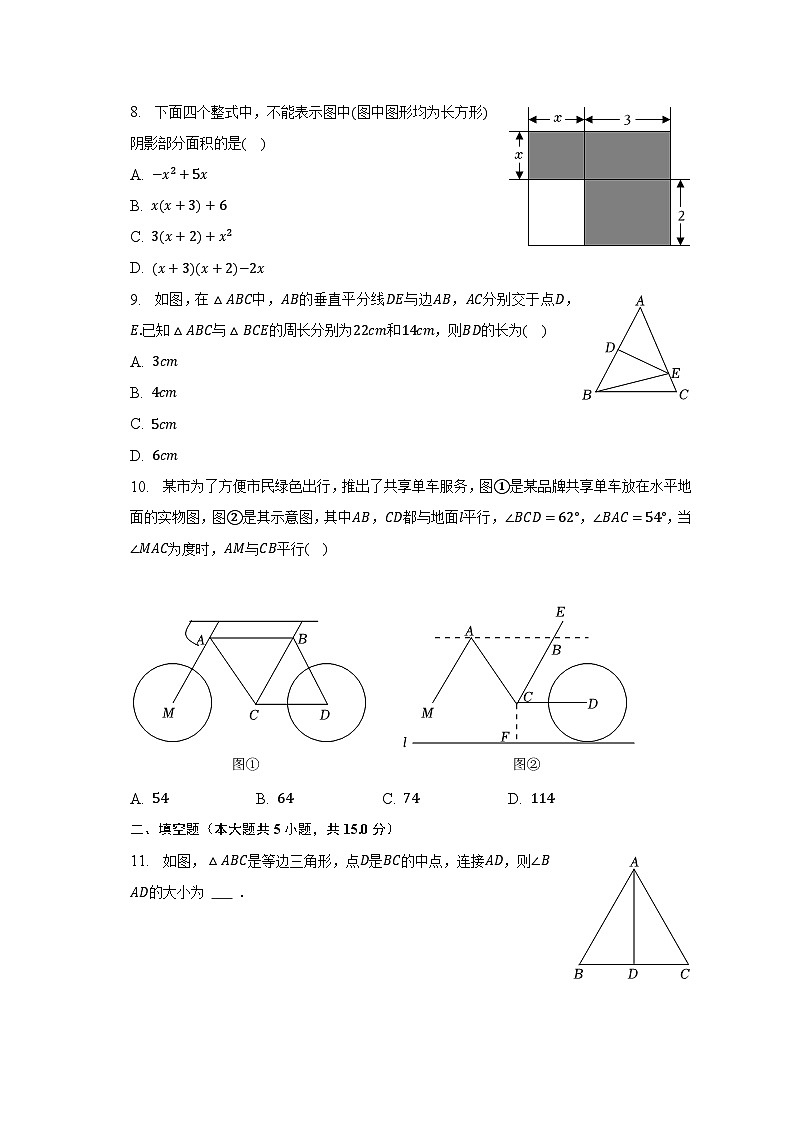
8. 下面四个整式中，不能表示图中(图中图形均为长方形)阴影部分面积的是(    )
A. −x2+5x
B. x(x+3)+6
C. 3(x+2)+x2
D. (x+3)(x+2)−2x
9. 如图，在△ABC中，AB的垂直平分线DE与边AB，AC分别交于点D，E.已知△ABC与△BCE的周长分别为22cm和14cm，则BD的长为(    )
A. 3cm
B. 4cm
C. 5cm
D. 6cm
10. 某市为了方便市民绿色出行，推出了共享单车服务，图①是某品牌共享单车放在水平地面的实物图，图②是其示意图，其中AB，CD都与地面l平行，∠BCD=62°，∠BAC=54°，当∠MAC为度时，AM与CB平行(    )


A. 54 B. 64 C. 74 D. 114
二、填空题（本大题共5小题，共15.0分）
11. 如图，△ABC是等边三角形，点D是BC的中点，连接AD，则∠BAD的大小为        ．


12. 如图，直线a/​/b，将一个直角的顶点放在直线b上，若∠1=50°，则∠2=        ．

13. 我国首辆火星车正式被命名为“祝融”，为应对极限温度环境，火星车使用的是新型隔温材料--纳米气凝胶，该材料导热率K(W/m⋅K)与温度T(℃)的关系如表：
温度T(℃)
100
150
200
250
300
导热率K(W/m⋅K)
0.15
0.2
0.25
0.3
0.35
根据表格中两者的对应关系，若导热率为0.5W/m⋅K，则温度为______ ℃.
14. 已知a+b=5，a2+b2=19，则ab=______．
15. 如图，在△ACD中，∠CAD=90°，AC=6，AD=8，AB/​/CD，E是CD上一点，BE交AD于点F，若EF=BF，则图中阴影部分的面积为______ ．
三、解答题（本大题共8小题，共75.0分。解答应写出文字说明，证明过程或演算步骤）
16. (本小题8.0分)
计算：(12)−1−(2023−π)0+2−2．
17. (本小题8.0分)
先化简，再求值：(2x+1)2+(x+1)(x−1)+(x4−4x3)÷x2，其中x=3．
18. (本小题8.0分)
如图，AB/​/CD，AE交CD于点F，DE⊥AE，垂足为E．
(1)若∠A=37°，求∠D的度数；
(2)直接写出图中与∠D互余的所有角．

19. (本小题9.0分)
小明和小芳都想参加学校社团组织的暑假实践活动，但只有一个名额，小明提议用如下的办法决定谁去参加活动：将一个均匀的转盘平均分成9等份，分别标上1至9这九个数字.转动转盘，当转盘停止后，指针指向的数字即为转出的数字．
(1)任意转动一次转盘，转出的数字是2的倍数的概率是多少？
(2)任意转动一次转盘，若转出的数字是2的倍数(6除外)，小明去参加活动；转出的数字是3的倍数(6除外)，小芳去参加活动；转出的数字是6或其它数字则重新转动转盘.你认为这个游戏公平吗？请说明理由．

20. (本小题9.0分)
已知：如图，A、C、F、D在同一直线上，AF=DC，AB/​/DE，AB=DE，求证：
(1)△ABC≌△DEF；
(2)BC//EF．

21. (本小题9.0分)
如图，点P是∠ABC内一点，PD//AB交BC于点D．
(1)利用尺规作图：过点P画BC的平行线交AB于点E.保留作图痕迹；
(2)在(1)的条件下，∠DPE等于∠B吗？请说明理由．

22. (本小题12.0分)
如图，在△ABC中，D是边AB上一点，E是边AC的中点，作CF/​/AB交DE的延长线于点F．
(1)证明：△ADE≌△CFE；
(2)若AB=AC，CE=6，CF=8，求DB的长．

23. (本小题12.0分)
甲、乙两车早上从A城车站出发匀速前往B城车站，在整个行程中，两车离开A城的距离s与时间t的对应关系如图所示：

(1)A，B两城之间距离是多少?
(2)求甲、乙两车的速度分别是多少?
(3)乙车出发多长时间追上甲车?
(4)从乙车出发后到甲车到达B城车站这一时间段，在何时间点两车相距40km?

答案和解析

1.【答案】D 
【解析】解：A、1+1<3，不能组成三角形，不符合题意；
B、1+3=4，不能组成三角形，不符合题意；
C、2+3<6，不能组成三角形，不符合题意；
D、6+6>9，能组成三角形，符合题意．
故选：D．
三角形的三条边必须满足：任意两边之和>第三边，任意两边之差<第三边，据此逐项解答即可．
本题主要考查对三角形三边关系的理解应用．判断是否可以构成三角形，只要判断两个较小的数的和>最大的数就可以．

2.【答案】C 
【解析】解：5.2×10−5=0.000052，
故选C．
只需将5.2的小数点向左平移5个数位即可．
本题考查求科学记数法的原数，掌握科学记数法法则是求解本题的关键．

3.【答案】B 
【解析】解：掷第4次时有6种等可能出现的结果，其中结果是“6”的有1种，
∴第4次的结果是“6”的概率是16，
故选：B．
直接由概率公式求解即可．
本题考查概率公式，理解题意和概率的意义是解题的关键．

4.【答案】C 
【解析】解：∵∠A=65°，∠C=15°，
∴∠ADC=180°−∠A−∠C=100°，
∵△ABE≌△ACD，
∴∠AEB=∠ADC=100°，
故选：C．
先利用三角形的内角和定理可得∠ADC=100°，然后利用全等三角形的性质即可解答．
本题考查了全等三角形的性质，熟练掌握全等三角形的性质是解题的关键．

5.【答案】C 
【解析】解：A、a3⋅a2=a3+2=a5，故本选项不符合题意；
B、a3与a2不能合并，故本选项不符合题意；
C、(3a3)2=9a6，故本选项符合题意；
D、a8÷a2=a6，故本选项不符合题意．
故选：C．
先根据合并同类项法则，同底数幂的乘除法法则，幂的乘方法则计算，再判断即可．
本题考查了合并同类项，同底数幂的乘除法法则以及幂的乘方法则，解题的关键是掌握相关运算法则并熟练运用．

6.【答案】B 
【解析】解：由题意得：流出的油量是0.2t升，油流完需要20÷0.2=100(分钟)，
则剩余油量：Q=20−0.2t(0≤t≤100)．
故选：B．
根据等量关系：油箱中存油量20升−流出油量=剩余油量，列出关系式即可．
此题主要考查了用关系式表示变量间的关系，关键是正确理解题意，找出题目中的等量关系．

7.【答案】D 
【解析】解：∵把一张长方形的纸按图那样折叠后，B，C两点落在B1，C1处，
∴∠BEF=∠B1EF，
∵∠AEB1=70°，∠AEB1+∠BEF+∠AEB1=180°，
∴∠BEF=(180°−∠AEB1)=12×(180°−70°)=55°．
故选：D．
根据折叠的性质可得出∠BEF=∠B1EF，再根据∠AEB1=70°，即可得出∠BEF的度数．
本题考查的是平行线的性质以及翻折变换，注意翻折前后不变的边和角是解此题的关键．

8.【答案】A 
【解析】解：由图可得，
图中阴影部分的面积=x2+3x+6，故选项A错误，符合题意；
x2+3x+2×3=x2+3x+6，故选项B正确，不符合题意，
3(x+2)+x2=x2+3x+6，故选项C正确，不符合题意，
(x+3)(x+2)−2x=x2+3x+6，故选项D正确，不符合题意，
故选：A．
根据图形，可以用代数式表示出图中阴影部分的面积，本题得以解决．
本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式．

9.【答案】B 
【解析】解：∵DE是AB的垂直平分线，
∴EA=EB，AD=BD=12AB．
∵△BCE的周长是14cm，
∴BC+BE+EC=14cm，即AC+BC=14cm．
∵△ABC的周长是22cm，
∴AB+AC+BC=22cm，
∴AB=22−14=8(cm)，
∴BD=12AB=12×8=4(cm)．
故选：B．
根据线段的垂直平分线的性质得到EA=EB，根据三角形的周长公式计算即可得到结论．
本题主要考查了段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．

10.【答案】B 
【解析】解：∵AB，CD都与地面l平行，
∴AB/​/CD，
∴∠BAC+∠ACD=180°，
∴∠BAC+∠ACB+∠BCD=180°，
∵∠BCD=62°，∠BAC=54°，
∴∠ACB=64°，
∴当∠MAC=∠ACB=64°时，AM/​/CB．
故选：B．
根据平行线的判定定理与性质定理求解即可．
此题考查了平行线的判定与性质，熟记平行线的判定定理与性质定理是解题的关键．

11.【答案】30° 
【解析】解：∵△ABC是等边三角形，
∴∠BAC=60°，
∵点D是BC的中点，
∴AD平分∠BAC，
∴∠BAD=12∠BAC=30°，
故答案为：30°．
根据等边三角形的三线合一性质求解即可．
此题考查了等边三角形的性质，熟记等边三角形的三线合一性质是解题的关键．

12.【答案】40° 
【解析】解：由图可知，∠3=180°−90°−∠1=180°−90°−50°=40°，

∵a/​/b，
∴∠2=∠3=40°，
故答案为：40°．
根据互余和两直线平行，同位角相等解答即可．
本题主要考查了平行线的性质以及互余的运用，解决问题的关键是掌握：两直线平行，同位角相等．

13.【答案】450 
【解析】解：根据题意，温度每增加50℃，导热率增加0.05W/m⋅K，
所以，当导热率为0.5W/m⋅K时，温度为450℃，
故答案为：450．
根据表格中两个变量T、K的对应值以及变化规律可得答案．
本题考查函数及其表示方法，理解函数的意义以及变量之间的变化规律是正确解答的关键．

14.【答案】3 
【解析】解：∵a+b=5，
∴(a+b)2=25，即a2+b2+2ab=25，
∴19+2ab=25，
解得：ab=3．
故答案是：3．
把a+b=5两边平方，然后把a2+b2=19代入即可求解．
本题主要考查完全平方公式的变形，熟记公式结构是解题的关键．完全平方公式：(a±b)2=a2±2ab+b2．

15.【答案】24 
【解析】解：∵AB/​/CD，
∴∠B=∠DEF，
在△BAF和△EDF中，
∠B=∠DEFBF=EF∠AFB=∠DFE,
∴△BAF≌△EDF(ASA)，
∴S△BAF=S△DEF，
∴图中阴影部分的面积=S四边形ACEF+S△AFB=S△ACD=12⋅AC⋅AD=12×6×8=24．
故答案为：24．
证明△BAF≌△EDF(ASA)，则S△BAF=S△DEF，利用割补法可得阴影部分的面积．
本题考查了全等三角形的性质和判定，平行线的性质，三角形的面积，熟练掌握全等三角形的判定是关键．

16.【答案】解：(12)−1−(2023−π)0+2−2
=2−1+14
=54． 
【解析】先根据负整数指数幂、零指数幂的运算法则计算，再合并即可．
此题考查的是负整数指数幂、零指数幂的运算法则，掌握其运算法则是解决此题的关键．

17.【答案】解：(2x+1)2+(x+1)(x−1)+(x4−4x3)÷x2
=4x2+4x+1+x2−1+x2−4x
=6x2，
当x=3时，原式=6×32=54． 
【解析】根据整式的混合运算法则结合乘法公式进行化简，然后代入求值即可．
本题考查了整式混合运算−化简求值，熟练掌握整式的四则混合运算法则以及乘法公式是解本题的关键．

18.【答案】解：(1)∵AB/​/CD，
∴∠EFD=∠A=37°，
∵DE⊥AE，
∴∠DEF=90°，
∴∠EFD+∠D=90°，
∴∠D=90°−∠DFE=53°；
(2)∵∠CFA=∠EFD=∠A，∠EFD+∠D=90°，
∴∠A+∠D=90°，∠CFA+∠D=90°，
即∠CFA，∠A，∠EFD都与∠D互余． 
【解析】(1)根据平行线的性质求出∠EFD=∠A=37°，再利用直角三角形两锐角互余求出∠D的度数；
(2)根据(1)及对顶角相等的性质解答即可．
本题考查了平行线的性质，垂直的定义，余角的定义，正确理解平行线的性质是解题的关键．

19.【答案】解：(1)∵任意转动一次转盘，转出的数字共有1、2、3、4、5、6、7、8、9这9种等可能的结果，其中是2的倍数有2、4、6、8共4种可能，
∴P(转出的数字是2的倍数)=49；
(2)游戏不公平，理由如下：
任意转动一次转盘，转出的数字共有1、2、3、4、5、6、7、8、9这9种等可能的结果，其中是2的倍数有2、4、6、8共4种可能，3的倍数有3、6、9共3种可能，由于转到6时需要重新转动转盘，故6舍去．
∴小明去参加活动的概率P=39=13，
小芳去参加活动的概率P=29，
∵13≠29，
∴游戏不公平． 
【解析】(1)根据概率公式直接计算即可；
(2)根据概率公式分别求出小明、小芳去参加活动的概率，若概率相同，则公平，否则不公平．
本题考查概率公式，游戏的公平性，熟练运用概率公式是解题的关键．

20.【答案】证明：
(1)∵AF=CD，
∴AF−FC=CD−FC即AC=DF．
∵AB//DE，
∴∠A=∠D．
在△ABC和△DEF中，
AB=DE∠A=∠DAC=DF
∴△ABC≌△DEF(SAS)；
(2)∵△ABC≌△DEF(已证)，
∴∠ACB=∠DFE，
∴∠BCF=∠EFC，
∴BC/​/EF． 
【解析】(1)由AF=CD，可求得AC=DF，由AB/​/DE，可得∠A=∠D，利用SAS可证明△ABC≌△DEF；
(2)由全等三角形的性质可得∠ACB=∠DFE，再利用平行线的判定可证明BC/​/EF．
本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法是解题的关键，即SSS、SAS、ASA、AAS和HL．

21.【答案】解：(1)如图，PE为所作；

(2)∠DPE等于∠B．
理由如下：
∵PD/​/AB，
∴∠B=∠CDP，
∵PE/​/BC，
∴∠CDP=∠DPE，
∴∠DPE=∠B． 
【解析】(1)作∠DPE=∠CDP即可；
(2)根据平行线的性质得到∠B=∠CDP，∠CDP=∠DPE，然后利用等量代换得到∠DPE=∠B．
本题考查了作图−复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了平行线的判定与性质．

22.【答案】(1)证明：∵点E是边AC的中点，
∴AE=CE，
又∵CF/​/AB，
∴∠A=∠ACF，∠ADF=∠F，
在△ADE和△CFE中，
∠ADF=∠F∠A=∠ACFAE=CE，
∴△ADE≌△CFE(AAS)；
(2)解：∵△ADE≌△CFE，CF=8，
∴CF=AD=8，
∵AB=AC，点E是边AC的中点，CE=6，
∴AC=2CE=12，
∴AB=12，
∴DB=AB−AD=12−8=4． 
【解析】(1)先根据中点得出AE=CE，再根据平行线的性质得出∠A=∠ACF，∠ADF=∠F，即可证明△ADE≌△CFE(AAS)；
(2)根据全等三角形的性质得出CF=AD=8，进而得出AC=2CE=12，根据线段的和差得出DB=AB−AD=12−8=4．
本题考查全等三角形的判定与性质，平行线的性质，证明三角形全等是解题的关键．

23.【答案】解：(1)由图象可知A、B两城之间距离是300千米；
(2)由图象可知，甲的速度=3005=60(千米/小时)，
乙的速度=3003=100(千米/小时)，
∴甲、乙两车的速度分别是60千米/小时和100千米/小时；
(3)设乙车出发x小时追上甲车，
由题意：60(x+1)=100x，
解得：x=1.5，
∴乙车出发1.5小时追上甲车；
(4)设乙车出发后到甲车到达B城车站这一段时间内，甲车与乙车相距40千米时甲车行驶了m小时，
①当甲车在乙车前时，
得：60m−100(m−1)=40，
解得：m=1.5，
此时是上午6：30；
②当甲车在乙车后面时，
100(m−1)−60m=40，
解得：m=3.5，
此时是上午8：30；
③当乙车到达B城后，
300−60m=40，
解得：m=133，
此时是上午9：20．
∴分别在上午6：30，8：30，9：20这三个时间点两车相距40千米． 
【解析】(1)根据图象即可得出结论；
(2)根据图象求甲、乙车两车速度；
(3)由题意列方程解决问题；
(4)分两车相遇前和相遇后以及乙到达B城三种情况进行讨论即可．
本题考查一次函数的应用、行程问题等知识，解题的关键是学会利用函数解决实际问题，学会转化的思想，把问题转化为方程，属于中考常考题型．