2023年陕西省榆林市子洲县张家港希望中学中考数学模拟试卷（含解析）

这是一份2023年陕西省榆林市子洲县张家港希望中学中考数学模拟试卷（含解析），共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2023年陕西省榆林市子洲县张家港希望中学中考数学模拟试卷
一、选择题（本大题共7小题，共21.0分。在每小题列出的选项中，选出符合题目的一项）
1. −12的相反数是(    )
A. −12 B. 12 C. −2 D. 2
2. 国家统计局发布数据显示，2022年末全国人口1411750000人，比上一年末减少85万人，为61年来首次负增长.将数据1411750000用科学记数法表示为(    )
A. 14.1175×108 B. 1.41175×109 C. 0.141175×109 D. 1.41175×1010
3. 如图，把一张长方形纸片ABCD沿EF折叠，∠1=55°，则∠2=(    )
A. 55°
B. 70°
C. 60°
D. 65°


4. 计算(4a2b3)2的结果是(    )
A. 6a4b5 B. 8a4b6 C. 12a4b5 D. 16a4b6
5. 如图，点P为▱ABCD内任意一点，连接PA、PB、PC、PD，将▱ABCD分为4个小三角形，面积分别为S1，S2，S3，S4，则下列等式成立的是(    )
A. S1+S4=S2+S3
B. S1+S3=S2+S4
C. S1+S2=S3+S4
D. S1=S4+S2+S3
6. 一次函数y=x+3与一次函数y=kx+b(k,b为常数，且k≠0)的图象关于直线x=−1对称，k与b的值分别是(    )
A. k=−3，b=−1 B. k=3，b=−1
C. k=−1，b=1 D. k=1，b=1
7. 已知抛物线y=ax2+bx+c(a,b,c是常数，a≠0)经过点(−1,−1)，(0,1).当x=−2时，与其对应的函数值y>1.有下列结论：
①abc>0；
②关于x的方程有两个不等的实数根；
③a+b+c>7.其中，正确结论的个数是(    )
A. 3 B. 2 C. 1 D. 0
二、填空题（本大题共6小题，共18.0分）
8. 下列各数：π， 10， 25，0.8，1.2020020002…(相邻的两个2之间依次多一个0)中，其中是无理数的有______ 个.
9. 如图，正五边形ABCDE的对角线BD、CE相交于点F，则∠CFD的度数为______ ．


10. 如图，在△ABC中，AB=AC，DE垂直平分AB交AC于点D，交AB于点E，若BC=4，且△BDC的周长为10，则AE的长为______ ．


11. 中国古代数学家刘徽在《九章算术》中，给出了证明三角形面积公式的出入相补法，如图所示，在△ABC中，分别取AB，AC的中点D，E，连接DE，过点A作AF⊥DE，垂足为F，△ABC分割后拼接成矩形BCHG，若DE=4，AF=3.5，则△ABC的面积是______ ．


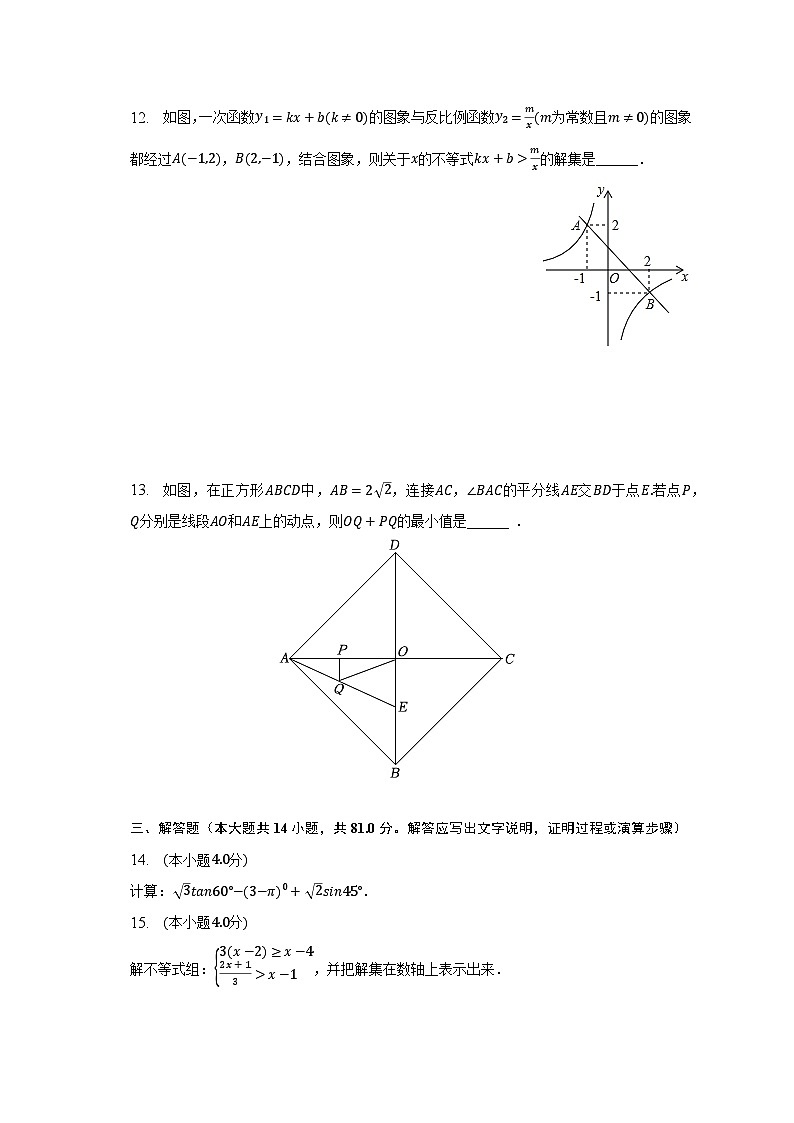
12. 如图，一次函数y1=kx+b(k≠0)的图象与反比例函数y2=mx(m为常数且m≠0)的图象都经过A(−1,2)，B(2,−1)，结合图象，则关于x的不等式kx+b>mx的解集是______．






13. 如图，在正方形ABCD中，AB=2 2，连接AC，∠BAC的平分线AE交BD于点E.若点P，Q分别是线段AO和AE上的动点，则OQ+PQ的最小值是______ ．

三、解答题（本大题共14小题，共81.0分。解答应写出文字说明，证明过程或演算步骤）
14. (本小题4.0分)
计算： 3tan60°−(3−π)0+ 2sin45°．
15. (本小题4.0分)
解不等式组：3(x−2)≥x−42x+13>x−1，并把解集在数轴上表示出来．
16. (本小题4.0分)
解分式方程：xx−2−1=6x2−4．
17. (本小题4.0分)
如图，已知∠BAC和边AB上一点D，且AP平分∠BAC.请利用尺规作图法在AP上找一点O，使∠AOD+∠OAC=90°.(不写作法，保留作图痕迹)

18. (本小题4.0分)
小惠自编一题：“如图，在四边形ABCD中，对角线AC，BD交于点O，AC⊥BD，OB=OD.求证：四边形ABCD是菱形”，并将自己的证明过程与同学小洁交流．
小惠：
证明：∵AC⊥BD，OB=OD，
∴AC垂直平分BD．
∴AB=AD，CB=CD，
∴四边形ABCD是菱形．
小洁：
这个题目还缺少条件，需要补充一个条件才能证明．
你赞同谁的证法？若赞成小洁的说法，请你补充一个条件，并证明．

19. (本小题5.0分)
“五一”国际劳动节，在这个属于劳动者的节日里，劳动的荣光分外耀眼，奋斗的强音激荡人心.劳动节当天，王老师组织学生参加社会实践活动，在如图所示的正方形ABCD苗圃中，分别栽种不同种类的树苗，其中，矩形EGHF的宽EF是6米，矩形MBCN的宽CN是4米，且矩形EGHF与矩形MBCN的面积相等，求矩形EGHF的面积．

20. (本小题5.0分)
如图，在平面直角坐标系中，△OAB的三个顶点的坐标分别为O(0,0)、A(4,1)、B(4,4)，将△OAB绕原点O顺时针旋转90°后得到△OA1B1(点A、B的对应点分别为点A1、B1).
(1)在图中画出△OA1B1；
(2)求线段OA绕原点O旋转到OA1扫过的面积(结果保留π)．

21. (本小题5.0分)
2023年4月24日，亚洲最大推力液体火箭发动机试验台在陕西正式建成投产，首次试车圆满成功.该试验台将为我国重型运载火箭、载人登月、深空探测等重大航天工程的顺利实施，提供有力动力保障.为激发学生弘扬爱国奋斗精神，以航天英雄为榜样，不断攀登新的科学高峰，某校举办以“相约浩瀚太空，逐梦航天强国”为主题的演讲比赛.九(1)班的宁宁和冬冬都想参加比赛，他们演讲水平相当，但名额只有一个.班委会商议后，决定用游戏的方式在他们二人中确定一名，班长准备了两个可以自由转动的转盘甲，乙，每个转盘被分成面积相等的几个扇形，在转盘甲每个扇形上分别标上数字1，2，3，4，在转盘乙每个扇形上分别标上数字−1，−2，−3.游戏规则：同时转动两个转盘，当转盘停止后，两个指针所指区域的数字之和为1时，宁宁获胜；数字之和为0时，冬冬获胜，其他情况视为平局.如果指针恰好指在分割线上，那么重转
一次，直到指针指向某一区域为止．
(1)用画树状图或列表法求冬冬获胜的概率；
(2)这个游戏规则对双方公平吗？请判断并说明理由．

22. (本小题6.0分)
西安大雁塔作为现存最早、规模最大的唐代四方楼阁式砖塔，它是佛塔这种古印度佛寺的建筑形式随佛教传入中原地区，并融入华夏文化的典型物证，凝聚了中国古代劳动人民智慧结晶的标志性建筑.小明同学想利用所学数学知识来测量大雁塔的高度，如图，小明在点B处放置一个平面镜，站在A处恰好能从平面镜中看到塔的顶端D，此时测得小明到镜面距离AB为2米，已知平面镜到塔底部中心的距离BC为86米，小明眼睛到地面距离AE为1.5米，已知AE⊥AC，CD⊥AC，点A、B、C在一条水平线上.请你帮小明计算出大雁塔CD的高度.(平面镜的大小忽略不计)

23. (本小题7.0分)
朗朗晴空、徐徐清风，民生之要、百姓之盼，某市深入贯彻生态文明思想，着力推动生态环境质量持续好转，努力绘就美丽中国画卷.市政府为了改善市内河流水质，市环保部门欲购买10台污水处理设备，现有A，B两种型号的设备，其中每台的价格，月处理污水量如下表，设购买A型号设备x台，购买这两种型号的设备共10台所需资金为y万元．

A型
B型
价格(万元/台)
12
10
每台设备处理污水量(吨/月)
220
200
(1)求y与x之间的函数关系式；
(2)若政府规定每月要求处理污水量不低于2040吨，为了节约资金，请你为环保部门设计一种最省钱的购买方案．
24. (本小题7.0分)
某社区倡议要美化小区环境，鼓励居民参与小区建设、提高广大群众爱绿护绿意识，打造绿色“爱心园区”，为了了解居民掌握“爱绿护绿”知识的情况进行调查.其中A、B两小区分别有500名居民参加了测试，社区从中各随机抽取50名居民成绩进行整理得到部分信息：
【信息一】A小区50名居民成绩的频数分布直方图如图(每一组含前一个边界值，不含后一个边界值)：

【信息二】上图中，从左往右第四组的成绩如下：
75
75
79
79
79
79
80
80
80
81
81
81
82
82
83
84
【信息三】A、B两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺)：
小区
平均数
中位数
众数
优秀率
方差
A
75
a
79
b
277
B
75
77
76
45%
211
根据以上信息，回答下列问题：
(1)填空：a= ______ ，b= ______ %；
(2)求A小区从左往右第四组的平均成绩，并估计A小区500名居民成绩能超过平均数75分的人数；
(3)请从两个角度，选择合适的统计量分析A，B两小区参加测试的居民掌握“爱绿护绿”知识的情况．
25. (本小题8.0分)
如图，⊙O是△ABC的外接圆，AB是⊙O的直径，点D在AC上，且BC=CD，接AD，AD与BC的延长线相交于点P，过点C作CE⊥AP于点E．
(1)求证：CE为⊙O的切线；
(2)若BC=6，⊙O的半径为5，求CE的长．

26. (本小题8.0分)
如图，抛物线y=ax2+bx+2的对称轴为x=−1，且与x轴交于A、B(2,0)两点．
(1)求抛物线的函数表达式；
(2)连接AC、BC，判断抛物线上是否存在点P，连接CP，使得CP将四边形CBPA的面积分为1：5两部分？若存在，求出点P的坐标；若不存在，请说明理由．

27. (本小题10.0分)
问题提出
(1)如图1，在梯形ABCD中，AD//BC，∠ABC=90°，AB=4，BC=6，CD=5，则AD的长为______ ；
问题探究
(2)如图2，在△ABC中，AE和CD分别是边BC、AB上的高，AB=95BC，若BD=2，求BE的长；
问题解决
(3)如图3，某地有一个半径为1km的圆形运动公园，为方便附近居民跑步锻炼身体，现要沿四边形ABCD的边铺设橡胶跑道(跑道的宽度忽略不计)，其中AB是⊙O的直径，点C，D在⊙O上，CD//AB.根据规划要求跑道ABCD的长度尽可能的大(即四边形ABCD的周长尽可能的大)，则四边形ABCD的周长是否存在最大值？若存在，请求出最大值；若不存在，请说明理由．


答案和解析

1.【答案】B 
【解析】解：−12的相反数是12，
故选：B．
根据只有符号不同的两个数互为相反数，可得答案．
本题考查了相反数，在一个数的前面加上负号就是这个数的相反数．

2.【答案】B 
【解析】解：1411750000=1.41175×109，
故选：B．
将一个数表示成a×10n的形式，其中1≤|a|1．
∴4a−2b+1>1，
∴4(b−2)−2b+1>1，解得：b>4，
∴a=b−2>0，
∴abc>0，故①正确；
②∵a=b−2，c=1，
∴(b−2)x2+bx+1−3=0，即(b−2)x2+bx−2=0，
∴Δ=b2−4×(−2)×(b−2)=b2+8b−16=b(b+8)−16，
∵b>4，
∴Δ>0，
∴关于x的方程ax2+bx+c−3=0有两个不等的实数根，故②正确；
③∵a=b−2，c=1，
∴a+b+c=b−2+b+1=2b−1，
∵b>4，
∴2b−1>7，
∴a+b+c>7．
故③正确；
故选：A．
①当x=0时，c=1，由点(−1,−1)得a=b−2，由x=−2时，与其对应的函数值y>1可得b>4，进而得出abc>0；
②将a=b−2，c=1代入方程，根据根的判别式即可判断；
③将a=b−2，c=1代入a+b+c，求解后即可判断．
本题考查二次函数的图象与性质，根的判别式；熟练掌握二次函数图象上点的特征，逐一分析三条结论的正误是解题的关键．

8.【答案】3 
【解析】解： 25=5，
在π， 10， 25，0.8，1.2020020002…(相邻的两个2之间依次多一个0)中，其中无理数是π， 10，1.2020020002…(相邻的两个2之间依次多一个0)，共有3个．
故答案为：3．
无限不循环小数是无理数，象π，开方开不尽的数，有规律但不循环的数都是无理数，从而可以解答．
本题考查了无理数和算术平方根，熟练掌握无理数的定义是解题的关键．

9.【答案】108° 
【解析】解：∵五边形ABCDE为正五边形，
∴∠BCD=∠CDE=(5−2)×180°÷5=108°，BC=CD=DE，
∴∠BDC=∠CBD=∠DCE=∠CED=180°−108°2=36°，
∴∠CFD=180°−∠BDC−∠DCE=180°−36°−36°=108°，
故答案为：108°．
利用多边形内角和公式及正多边形性质求得∠BCD，∠CDE的度数，再利用等边对等角及三角形内角和定理求得∠BDC，∠DCE的度数，然后再利用三角形内角和定理即可求得答案．
本题考查多边形的内角和及正多边形的性质，等腰三角形性质，结合已知条件求得∠BCD，∠CDE的度数是解题的关键．

10.【答案】3 
【解析】解：∵DE垂直平分AB，
∴DA=DB，
∵△BDC的周长为10，
∴BD+DC+BC=AD+CD+BC=AC+BC=10，
∵BC=4，
∴AC=6，
∴AB=AC=6，
∴AE=12AB=3．
故答案为：3．
由线段垂直平分线的性质，得到DA=DB，推出AC+BC=10，求出AC的长，得到AB的长，即可求出AE的长．
本题考查等腰三角形的性质，线段垂直平分线的性质，关键是由线段垂直平分线的性质定理得到AC+BC=10，求出AC的长．

11.【答案】12． 
【解析】解：由题意，BG=CH=AF=3.5，DG=DF，EF=EH，
∴DG+EH=DE=4，
∴BC=GH=4+3.5=7.5，
∴△ABC的边BC上的高为4，
∴S△ABC=12×6×4=12，
故答案为：12．
根据图形的拼剪，求出BC以及BC边上的高即可解决问题．
本题考查图形的拼剪，矩形的性质，全等三角形的判定和性质，三角形的面积等知识，解题的关键是读懂图象信息．

12.【答案】x