13.1轴对称精讲精练设计人教版八年级上册数学

这是一份13.1轴对称精讲精练设计人教版八年级上册数学，共5页。
精讲精练设计——轴对称 一、核心概要    1.轴对称图形是具有特殊形状的一个图形，而轴对称指的是两个图形之间的        .如果把轴对称图形沿对称轴分成两个图形，这两个图形就关于这条直线成轴对称.反过来，如果把两个成轴对称的图形看成一个整体，那么它就是一个        .   2.线段垂直平分线上的点与这条线段两个端点的距离     .与线段两个端点距离相等的点，在这条线段的           .因此，线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合.   3.如果两个图形成轴对称，那么对称轴是任何一对对应点所连线段的             .类似地，轴对称图形也具有此性质.二、典例精讲   例1 如图①，请在直线 l上找到一点P，使得 A，B 两点到点 P 的距离之和最短.  

   分析：结合轴对称的性质，先画出点 A 关于直线l的对称点A'，连接 BA'， BA'与直线l的交点就是所找的点P 的位置，因为点 P 到点A 与点P 到点A'的距离相等，其他的任何点都不满足 B，P，A'三点在同一直线上.本题紧扣轴对称的性质，是一道结合轴对称的性质解决线段和最短问题的典型例题.这一性质的运用，既是本题的切入点，同时也是难点所在.解:如图②,(1)作点 A 关于直线l的对称点A';(2)连接 BA'交直线 l于P.点 P 即为所求.证明:如图②,在直线 l上任取一点 P'(异于点 P),连接AP',A'P',BP',AP.将 PA+PB与            比较可知，因为在△A'BP'中, 故    例2 如图,在△ABC中,AB=AC,DF 垂直平分AB 交 AC 于F,AB+ BC=6,求△BCF 的周长. 分析:AF,BF 关于DF 对称,所以 AF=BF,AC=BF+CF=AB,△BCF的周长等于AB+BC 的和.本题无需说明△AFD≌△BFD，直接利用线段垂直平分线的性质解答.解:因为DF 垂直平分AB,所以AF=BF,则△BCF 的周长为:
CF+CB+BF=CF+CB+AF=CB+AC=AB+BC=6. 例3 如图,线段 AB,BC 的垂直平分线 l₁,l₂相交于点 O,若∠1=39°,求∠AOC 的大小.分析：由点O为线段AB，BC 的垂直平分线的交点，可知 OA=OB=OC，再利用多边形内角和计算.解:过点 O 作射线BP,如图.
∵线段 AB,BC 的垂直平分线 l₁,l₂相交于点O,∴AO=OB=OC,∠BDO=∠BEO=90°.∴∠DOE+∠ABC=180°.∵∠DOE+∠1=180°,∴∠ABC=∠1=39°.∵OA=OB=OC,∴∠A=∠ABO,∠OBC=∠C.∵∠AOP=∠A+∠ABO,∠COP=∠C+OBC,∴∠AOC=∠AOP+∠COP=∠A+∠ABC+∠C=2×39°=78°.
三、分级作业A级   1.中国的方块字中有些具有对称性.下面4个汉字中是轴对称图形的是(   ).A.爱     B.我     C.中     D.华2.下列图形中，只有两条对称轴的是(   ).A.等边三角形  B.平行四边形     C.矩形     D.圆   3.小军同学在网格纸上将某些图形进行平移操作，他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示，现在他将正方形 ABCD 从当前位置开始进行一次平移操作，平移后的正方形顶点也在格点上，则使平移前后的两个正方形组成轴对称图形的平移方向有(   ).A.3个           B.4个           C.5个           D.无数个   4.如图,在△ABC 中,AD 垂直平分边 BC,若 AB=6,则 AC 的长度为     .5.         具有无数条对称轴.(写出一种图形名称即可)   6.如图,在 Rt△ABC中,∠C=90°,DE 垂直平分 AB,且∠BAD:∠DAC=1:3.求∠B 的度数. 7.如图,已知在△ABC 中,AH⊥BC 于点 H,∠C=35°,且 AB+BH= HC.求∠B 的度数.   8.如图，网格上是由个数相同的白色方块与灰色方块组成的一幅图案.请仿照此图案，在旁边的网格中设计出一个轴对称图案(不得与原图案相同，灰、白方块的个数要相同).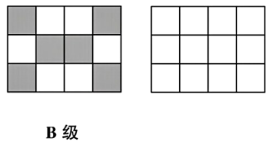    9.如图,将△ABC 折叠,使点 A 与 BC边中点D重合,折痕为 MN,若AB=9,BC=6,则△DNB 的周长为( ).   A.12        B.13         C.14            D.15 10.如图,直线 l 是四边形 ABCD 的对称轴,如果有 AD= BC,有下列结论:①AB∥CD;②AB=BC;③AC⊥BD;④AO=OC.其中正确的结论是         _____________(填序号).              11.如图,在四边形 ABCD中,∠DAB=∠ABC=90°,E为AB的中点,AB=BC,CE⊥BD.               (1)求证: AC 垂直平分线段 DE.(2)求证:∠DBC=∠DCB.       12.如图,在△ABC中,∠C=30°,AC 的垂直平分线EF 交AC 于点E,交 BC 于点 F,且BF=2FC.求证∠B=30°.    四、探究天地   13.如图,在△ABC 中,∠BAC 的平分线AD与BC 边的垂直平分线 DE 交于点D,DG⊥AB,DH⊥AC,G、H为垂足.(1)求证 BG=CH.(2)线段 AB，AC 与 BG之间有何数量关系?证明你的结论.