湘教版八年级下册1.3 直角三角形全等的判定公开课教学设计

第1章 直角三角形

1.3 直角三角形全等的判定

【知识与技能】

1.已知斜边和直角边会作直角三角形.

2.熟练掌握“斜边、直角边公理”，以及熟练地利用这个公理和判定一般三角形全等的方法判定两个直角三角形全等.

3.熟练使用“分析综合法”探求解题思路.

【过程与方法】

通过探究性学习，营造民主和谐的课堂气氛，初步学会科学研究的思维方法；通过一题多变、一题多解，培养学生的发散思维能力，增强学生的创新意识和创新能力；通过实践探究，培养学生读题、识图能力，提高学生观察与分析，归纳与概括的能力.

【情感态度】

通过对一般三角形与直角三角形全等判定方法的比较，初步感受普遍性与特殊性之间的辩证关系；在探究性学习活动中培养学生刻苦钻研、实事求是的态度，勇于探索创新的精神，增强学生的自主性和合作精神.

【教学重点】

“斜边、直角边公理”的掌握和灵活运用.

【教学难点】

数学语言的正确表达.

一、创设情境，导入新课

问题1  说出判定一般三角形全等的依据，并说出它们的共同点.

问题2  有斜边和一直角边对应相等的两个直角三角形是否全等？

【教学说明】

在学生已经掌握了一般三角形全等的判定方法的基础上，给学生提出特殊的直角三角形的判定方法，容易接受理解，学习起来比较轻松.教师讲课前，先让学生完成预习.

二、思考探究，获取新知

问题1  斜边、直角边定理的证明.

例：教材第19页“探究”

【教学说明】

让学生明白斜边、直角边定理是由勾股定理推理得出的第三条边相等，从而利用三边证明两个直角三角形全等的特殊方法.

问题2 “HL”定理的运用

例： 教材第20页例1

【教学说明】

通过学习，学生弄清了利用“HL”证明两个直角三角形全等的书写格式和证明途径.

问题3  用尺规作一个直角三角形

例： 教材第20页例2

【教学说明】

通过学生的动手操作、交流、讨论，掌握已知一条斜边和一直角边作一个直角三角形的方法，体验学习数学的过程.

三、运用新知，深化理解

1.如图，AB=AC，BD⊥AC于D，CE⊥AB于E，则图中全等的三角形对数为（    ）

A.1    B.2    C.3    D.4

2.如图，AC⊥BC，BD⊥AD，AC、BD相交于O，如果AC=BD，那么下列结论中：①AD=BC；②∠DAC=∠CBD；③OC=OD.其中正确的有（   ）

A.①②③  B.①②  C.①②  D.③

3.下列条件中，不能作出唯一直角三角形的是（  ）

A.已知两条直角边

B.已知两个锐角

C.已知一条直角边和斜边

D.已知一个锐角和一条直角边4.在Rt△ABC中，∠ACB=90°，BC=2cm，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F，若EF=5cm，则AE=cm.

5.如图，AC⊥AD，BC⊥BD，OE⊥CD，AC=BD，求证：DE=CE.

【教学说明】

学生自主完成，加强对所学知识的理解，教师可以根据学生掌握的情况有针对性地加以矫正强化.在完成上述题目后，让学生完成练习册中本课时 的对应训练部分.

答案：1.C   2.A   3.B    4.3  

5.∵AC⊥AD，BC⊥BD，∴∠A=∠B=90°，在Rt△ADC和Rt△BCD中，DC=CD，AC=BD，

∴Rt△ADC≌Rt△BCD（HL），

∴∠ACD=∠BDC.在Rt△ODE和Rt△OCE中，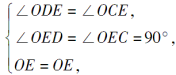

∴Rt△ODE≌Rt△OCE（AAS），∴DE=CE.

四、师生互动，课堂小结

通过今天的学习，你能说出判定两个直角三角形全等有哪些方法吗？还存在哪些不足?请与大家共同交流.

【教学说明】

及时梳理知识，不断总结归纳直角三角形全等的判定方法，让学生看到自己的进步，提高学生的学习热情.

1.布置作业：习题1.3中的第2、3、4题.

2.完成练习册中本课时练习的作业部分.

在教学的过程中，利用“HL”定理学生往往容易忽略证明两个直角三角形全等的前提条件是直角三角形,以后的教学中要加以强调，同时学生利用尺规作直角三角形还不是很熟练，注重他们的动手操作能力.