湘教版八年级下册1.4 角平分线的性质公开课第2课时教学设计

这是一份湘教版八年级下册1.4 角平分线的性质公开课第2课时教学设计，共3页。教案主要包含了知识与技能，过程与方法，情感态度，教学重点，教学难点，教学说明等内容，欢迎下载使用。
1.4 角平分线的性质第2课时 角平分线性质定理及其逆定理的综合应用【知识与技能】让学生在掌握角平分线的性质的基础上能应用角平分线的两个性质解决一些简单的实际问题.【过程与方法】通过让学生经历动手实践，合作交流，演绎推理的过程，使学生学会理性思维，从而提高解决简单问题的能力.【情感态度】经历对角的平分线的性质的探索与形成的过程，发展应用数学知识的意识与能力，培养学生的联想、探索、概括归纳的能力，激发学生学习数学的兴趣.【教学重点】角平分线的性质及其应用【教学难点】灵活应用两个性质解决问题一、创设情境，导入新课问题  一个S区有一个贸易市场，在公路与铁路所成角的平分线上有一点P，要从P点建两条路，一条到公路上，一条到铁路上，怎样修建路最短？这两条有什么关系？画出来看一看.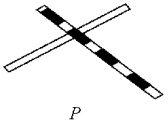【教学说明】让学生动手画出最短的路线，可以复习点到直线的距离这一知识点，为探究角的平分线的性质作铺垫，同时也让学生感受到数学与实际生活是紧密相联的，从而激发学生学习兴趣，体现有价值的数学.教师讲课前，先让学生完成预习.二、思考探究，获取新知问题  角平分线性质与判定的应用思考  教材第24页“动脑筋”【教学说明】让学生明白要找角平分线只需要找角的内部某一点到角两边的距离相等即可，从而找到解决问题的方法.例： 教材第25页例2【教学说明】既复习了三边关系，又能巩固加深了角平分线性质的应用.思考  教材第25页“动脑筋”【教学说明】通过学生合作、探究得出三角形的角平分线是相交于一点的，同时等式的传递性也得到了充分利用.三、运用新知，深化理解1.如图，AB=AC，BE⊥AC于E，CF⊥AB于F，BE、CF相交于D，则下列结论：①△ABE≌△ACF；②△BDF≌△CDE；③点D在∠BAC的平分线上，其中正确的是（    ）A.只有①    B.只有②   C.只有①和②    D.①②③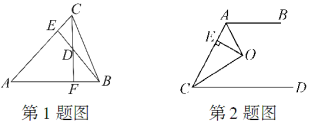2.如图所示，已知AB∥CD，O是∠BAC与∠ACD的平分线的交点，OE⊥AC于E，OE=2，则AB与CD之间的距离为_______.3.如图，△ABC中，试证明:（1）若AD为∠BAC的平分线，则S△ABD∶S△ACD=AB∶AC；（2）设D为BC上的一点，连接AD.若S△ABD∶S△ACD=AB∶AC，则AD为∠BAC的平分线.【教学说明】由学生独立完成，对有困难的学生给予指导，及时更正他们发生的错误，根据学生掌握程度必要时加强训练.在完成上述题目后，让学生完成练习册中本课时 的对应训练部分.答案：1.D  2.4 3.证明：（1）过点D作DE⊥AB于点E，DF⊥AC于点F.∵AD平分∠BAC，且DE⊥AB，DF⊥AC，∴DE=DF，∴S△ABD∶S△ACD=(1/2AB·DE)∶(1/2AC·DF)=AB∶AC.(2)∵S△ABD∶S△ACD=（1/2AB·DE）∶（1/2AC·DF）=AB∶AC，∴DE=DF.又∵DE⊥AB，DF⊥AC，∴AD为∠BAC的平分线.四、师生互动，课堂小结通过本节课的学习，你掌握了哪些内容？还存在什么疑惑？与大家共同分享.【教学说明】及时反馈学生的掌握情况，让学生看到自己的进步，激励学生相信自己的能力，促进学生良好的心理品质.1.布置作业：习题1.4中的第4、5题.2.完成练习册中本课时 练习的作业部分.对于利用角平分线的性质和判定进行有关的证明，学生掌握情况较好，就是与角平分线有关的面积计算问题，还不够熟练，以后的教学中对此加强训练.