第2章四边形2.3中心对称和中心对称图形第1课时中心对称概念及性质教案（湘教版八下）

2.3  中心对称和中心对称图形

第1课时  中心对称概念及性质

【知识与技能】

1.了解中心对称、对称中心和对称点的概念.

2.理解中心对称的性质.

3.掌握运用中心对称的性质作图的方法.

【过程与方法】

通过对中心对称的性质的探究及运用，初步学会从正反两方面去思考问题的数学思考方法，以及类比思想的应用.

【情感态度】

通过一系列探索活动，培养学生严谨的科学态度和探索的精神；经历数学知识融于生活实际的实习过程，体验数学学习的快乐.

【教学重点】

中心对称的概念；中心对称的性质；利用中心对称的性质进行作图.

【教学难点】

中心对称与轴对称的区别与联系，利用中心对称的性质准确作图.

一、创设情境，导入新课

提问  （1）把图（1）中的一个图案绕点O旋转180°，你有什么发现？

（2）如图（2），线段AC、BD相交于点O，OA=OC，OB=OD，把△OCD绕点O旋转180°，你有什么发现？

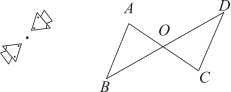
【教学说明】通过显示图形变化，导入课题可以吸引学生的注意力.同时让学生通过有声有色的图形变换，引出概念，学生接收快.教师讲课前，先让学生完成预习.

二、思考探究，获取新知

问题1  中心对称、对称中心和对称点的概念

做一做  教材第51页图2-31

【教学说明】通过实际操作，感受图形变化，直观的得出有关概念，易于学生理解.

问题2  中心对称的性质

阅读  教材第51页第四段及方框内容并作图

【教学说明】让学生自己动手画图，进一步加深对中心对称的理解，通过观察得出中心对称的性质，为下一步的学习打好基础.

例：教材第51页“例题”

【教学说明】运用性质，寻找对应点，让学生学会作一个关于某点成中心对称的图形，并得以运用.

三、运用新知，深化理解

1.如图所示的4组图形中，右边的图形与左边的图形成中心对称的是（    ）

2.如图，△ABC与△A′B′C′关于点O成中心对称，则下列结论不成立的是（    ）

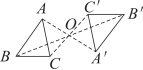A.点A与点A′是对称点

B.BO=B′O

C.AB∥A′B′

D.∠ACB=∠C′A′B′

3.已知A、B、O三点不在同一条直线上，A、A′关于点O对称，B、B′关于点O对称，那么线段AB与A′B′的关系是      ，若连接AB′、BA′，则四边形ABA′B′是        形.

4.已知∠ABC内有一点P，作出∠ABC关于点P的对称图形.

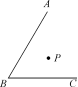
【教学说明】由学生自主完成，加深了对所学知识的理解与运用，便于教师掌握情况，做到及时辅导，并有针对性地加强训练.在完成上述题目后，让学生完成练习册中本课时的对应训练部分.

答案：1.A    2.D 

3.ABA′B′,平行四边

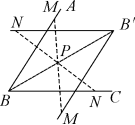
4.（1）如图所示，连接BP并延长到B′，使BP=B′P，则B′为B的对称点；

（2）在AB、BC上取M、N点，同理画出M、N的对称点M′、N′；

（3）连结B′M′、B′N′，得到∠M′B′N′，即为∠ABC关于点P的对称图形.

四、师生互动，课堂小结

经过这节课的学习，你能作出一个关于某点的中心对称图形吗？有哪些收获？还存在哪些困难？请与同学们探讨.

【教学说明】回顾所学知识，做到整体认识，突出方法总结，让学生掌握规律，同学之间相互学习，共同进步.

1.布置作业：习题2.3中的第1、4题.

2.完成练习册中本课时练习的作业部分.

通过练习的情况来看，学生对于中心对称的作图掌握较好，解题也相当熟练，而对于中心对称、对称中心等概念的理解上还不透彻，有些模棱两可，在以后的教学中要通过实例或图形不断加以强化.